FFT频谱分析

Python进行FFT频谱分析

声明：本文思想均来自陈爱军老师《深入浅出通信原理》连载313-389

连载354

目录

FFT点数分析

连载543

FFT点数 = OFDM符号周期 x 采样频率

OFDM符号周期 = 1/子载波间隔

Cosine信号波形

DFT公式: $X(k)=frac{1}{N} sum_{n=0}{N-1}x(n)e{-jfrac{2pi}{N}kn} $

由常识可知(cos(2pi ft))的频谱在1和-1处均有1/2的值，如下所示

即实数信号有对称的频谱形状

# cosine wave(cos2pit) 进行 DFT
plt.subplot(2,1,1)
t = np.arange(0,1.01,0.01)
f = np.cos(2*np.pi*t)
plt.plot(t,f)
plt.xlabel('t')
plt.ylabel('magnitude')
plt.title('cosine wave')
N = 10
n = np.arange(0,N,1)
f = np.cos(2*np.pi*n/N)
t = np.arange(0,1,0.1)
plt.stem(t,f,use_line_collection=True)

# N=10, Ts=0.1s
plt.subplot(2,1,2)
n = np.arange(0,N,1)
x = np.cos(2*np.pi*n/N)
c = []
for k in np.arange(-N/2,N/2+1,1):
    S=0
    for n2 in n:
        S = S+x[n2]*np.exp(-1j*2*np.pi*k*n2/N)
    c.append(S/N)    
k = np.arange(-N/2,N/2+1,1)
plt.stem(k,c,use_line_collection=True)
plt.xlabel('f')
plt.ylabel('Magnitude')
plt.title('DFT of cosine wave')
plt.tight_layout()

cos(2pift)作DFT

直接调用FFT函数计算：

# 时域采样信号
plt.subplot(211)
N = 10
n = np.arange(0,N,1)
f = np.cos(2*np.pi*n/N)
t = np.arange(0,1,0.1)
plt.stem(t,f,use_line_collection=True)
plt.xlabel('t')
plt.ylabel('magnitude')
plt.title('cosine wave')
# 频谱信号
# REF: http://localhost:8888/notebooks/PycharmProjects/Untitled2.ipynb
plt.subplot(212)
S = np.fft.fft(f)/N
# 给出横坐标的数字频率, 第一个参数n是FFT的点数，一般取FFT之后的数据的长度（size）, 第二个参数d是采样周期，其倒数就是采样频率Fs，即d=1/Fs
n = np.fft.fftfreq(N, 1/N) 
# 用于将FFT变换之后的频谱显示范围从[0, N]变为：[-N/2, N/2-1](N为偶数)   或者 [-(N-1)/2, (N-1)/2](N为奇数)
S = np.fft.fftshift(S)
n = np.fft.fftshift(n)
plt.stem(n,S,use_line_collection=True)
plt.xlabel('f')
plt.ylabel('Magnitude')
plt.title('DFT of cosine wave')
plt.tight_layout()

fft函数分析cos信号

不限制频域范围[-2N,2N]，可见DFT后X(k)是周期为N的函数，因此通常取值区间取主值区间[-N/2,N/2]

# N=10, Ts=0.1s
plt.subplot(2,1,2)
n = np.arange(0,N,1)
x = np.cos(2*np.pi*n/N)
c = []
for k in np.arange(-N*2,N*2+1,1):
    S=0
    for n2 in n:
        S = S+x[n2]*np.exp(-1j*2*np.pi*k*n2/N)
    c.append(S/N)    
k = np.arange(-N*2,N*2+1,1)
plt.stem(k,c,use_line_collection=True)
plt.xlabel('f')
plt.ylabel('Magnitude')
plt.title('DFT of cosine wave')
plt.tight_layout()

X(k)是周期为N的函数

IDFT变换的本质是将信号的样本序列（N个样点）表示成1个直流样点序列，2/N个逆时针旋转的旋转向量样点序列和2/N-1个顺时针样点序列

k=9的样点数据与k=-1相同，因为(e^{jfrac{2pi}{N} kn})当 k=N/2+i 和 k=-N/2+i 相同

周期方波信号波形

# 周期方波作FFT
plt.figure(figsize=(6,10))
plt.subplot(511)
N = 40
x1 = np.ones(int(N/4))
x2 = np.append(x1,np.zeros(int(N/2)+1))
x3 = np.append(x2,np.ones(int(N/4)-1))
n = np.arange(0,len(x3),1)
plt.stem(n,x3,use_line_collection=True) # 偶对称的周期方波
plt.title("偶对称的周期方波",fontproperties='stsong')

plt.subplot(512)
X = np.fft.fft(x3)/N
plt.stem(n,X,use_line_collection=True) # 默认只画实部
plt.title("偶对称的周期方波FFT实部",fontproperties='stsong')

# 虚部
plt.subplot(513)
plt.stem(n,np.imag(X),use_line_collection=True)
plt.title("偶对称的周期方波FFT虚部",fontproperties='stsong')

# IFFT
# plt.subplot(5,1,3)
x = np.fft.ifft(X)
# plt.stem(n,x,use_line_collection=True)
# plt.title("IFFT",fontproperties='stsong')

# 幅度谱, 和连载347的不同
plt.subplot(514)
plt.stem(n,abs(X),use_line_collection=True)
plt.title("偶对称的周期方波FFT幅度谱",fontproperties='stsong')
# 相位谱
plt.subplot(515)
plt.stem(n,np.angle(X),use_line_collection=True)
plt.title("偶对称的周期方波FFT相位谱",fontproperties='stsong')
plt.tight_layout()

周期方波频谱图

复合信号进行FFT(补零，截断加长，加窗)

(f(t) = cos(200 pi t)+sin(100 pi t)+cos(50 pi t)) 进行频谱分析

# 连载354
fs = 400 #采样频率
T = 0.04 #截取总时间
N = fs*T #采样16个点
t = np.arange(0,T,1/fs)
x = np.cos(200*np.pi*t)+np.sin(100*np.pi*t)+np.cos(50*np.pi*t)
plt.subplot(311)
plt.stem(t,x,use_line_collection=True)
plt.title('$f(t) = cos(200 pi t)+sin(100 pi t)+cos(50 pi t)$')

plt.subplot(312)
X = np.fft.fft(x)
# n = np.arange(0,fs,fs/N) # 16个点，频谱宽度400Hz
n = np.fft.fftfreq(int(N),1/fs)
X = np.fft.fftshift(X)
n = np.fft.fftshift(n)
plt.stem(n,abs(X),use_line_collection=True)
plt.title('Magnitude Spectrum')
plt.tight_layout()

复合信号频谱

显然该信号频谱很完美，但若要提高频谱密度如何做？

答案：补零，将16个采样点补零至256个采样点

其实质是增大信号周期

# 采样数据后补0来提高频谱密度，即增大时域信号周期
fs = 400 #采样频率
T = 0.04 #截取总时间
N = fs*T #采样16个点
t = np.arange(0,T,1/fs)
x = np.cos(200*np.pi*t)+np.sin(100*np.pi*t)+np.cos(50*np.pi*t)
t2 = np.arange(T,0.64,1/fs)
t = np.append(t,t2)
x = np.append(x,np.zeros(len(t2))) #补0增大频谱密度
plt.subplot(311)
# plt.stem(t,x,use_line_collection=True)
plt.plot(t,x)
plt.title("补零增加频谱密度的f(t)",fontproperties='stsong')

plt.subplot(312)
X = np.fft.fft(x)
n = np.arange(0,400,fs/N/N) # 16个点，频谱宽度400Hz
plt.stem(n,abs(X),use_line_collection=True) # 显然此时频谱分辨率降低
plt.title("有旁瓣泄露的频谱",fontproperties='stsong')
# plt.plot(n,abs(X))
plt.tight_layout()

增大频谱密度

频谱密度提高了，但是频谱分辨率显然下降，出现旁瓣泄露

那么如何提高分辨率呢？很明显，增加截取长度即可

# 增加信号周期数提高频谱分辨率
fs = 400 #采样频率
T = 0.16 #截取总时间，四个周期
N = fs*T #采样64（Not 16）个点
t = np.arange(0,T,1/fs)
x = np.cos(200*np.pi*t)+np.sin(100*np.pi*t)+np.cos(50*np.pi*t)
t2 = np.arange(T,0.64,1/fs)
t = np.append(t,t2)
x = np.append(x,np.zeros(len(t2))) #补0增大频谱密度
plt.subplot(311)
# plt.stem(t,x,use_line_collection=True)
plt.plot(t,x)
plt.title("增加4倍信号截取长度增加频谱分辨率的f(t)",fontproperties='stsong')

plt.subplot(312)
X = np.fft.fft(x)
n = np.arange(0,fs,fs/256) # 32个点，频谱宽度400Hz
# plt.stem(n,abs(X),use_line_collection=True) # 显然此时频谱分辨率降低
plt.plot(n,abs(X)[:256]) # 此时存在的非信号频谱分量就是泄露效应
plt.title("分辨率提高的频谱)",fontproperties='stsong')
plt.tight_layout()

提高f(t)频谱分辨率

除了原信号确实存在的频率分量外还存在原信号中没有的频率分量，这就是泄露效应

泄露效应与截断长度相关，截取长度越长，分辨率越高，泄露越少

截断的过程就是与矩形窗相乘的过程，我们分析的频谱是原始信号与矩形窗信号乘积再补零的频谱

plt.figure(figsize=(6,6))
# 原信号f(t)
plt.subplot(3,1,1)
fs = 400 #采样频率
T = 0.04*8 #周期数目
N = fs*T #采样点数
t = np.arange(-T/4,3*T/4,1/fs)
f = np.cos(200*np.pi*t)+np.sin(100*np.pi*t)+np.cos(50*np.pi*t)
plt.stem(t,f,use_line_collection=True)
plt.plot(t,f,color='r')
plt.title('$f(t) = cos(200 pi t)+sin(100 pi t)+cos(50 pi t)$')

# 矩形窗w(t)
plt.subplot(312)
w1 = np.zeros(int(N/4))
w2 = np.ones(int(N/2))
w = np.append(w1,w2)
w = np.append(w,w1)
plt.stem(t,w,use_line_collection=True)
plt.title('Rectangle Windows w(t)')

# 乘积信号
plt.subplot(313)
y = f*w
plt.stem(t,y,use_line_collection=True)
plt.title('f(t)*w(t)')
plt.tight_layout()

信号与矩形窗相乘

连载367

截取时长等于频率成分周期的整数倍，对采样序列进行周期性扩展得到的周期序列的周期正好等于频率成分的周期，可确保不出现泄露

采样频率也必须是信号频率的整数倍，否则也会造成信号泄露

且如上所示补零也会造成频谱泄露

频谱泄露条件.jpg

1.jpg

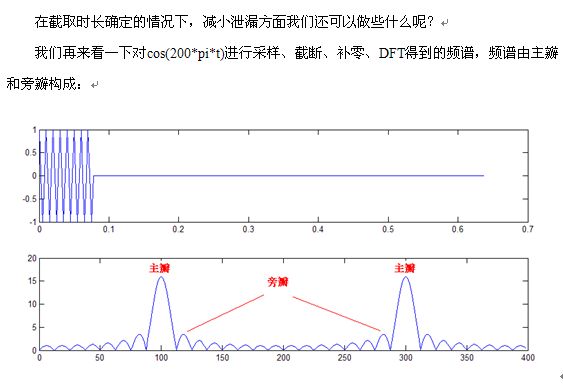
以对数角度来看，主瓣和旁瓣差别不大

plt.figure(figsize=(6,6))
# 原信号f(t)
plt.subplot(3,2,1)
fs = 400 #采样频率
T = 0.04*16 #周期数目
N = fs*T #采样点数
t = np.arange(0,T,1/fs)
f = np.cos(200*np.pi*t)
t = np.arange(0,N,1)
plt.stem(t,f,use_line_collection=True)
# plt.plot(t,f,color='r')
plt.title('$f(t) = cos(200 pi t)$')

# 矩形窗w(t)
plt.subplot(323)
w1 = np.ones(int(N/8))
w2 = np.zeros(int(N-N/8))
w = np.append(w1,w2)
plt.stem(t,w,use_line_collection=True)
plt.title('Rectangle Windows w(t)')

# 乘积信号
plt.subplot(325)
y = f*w
plt.stem(t,y,use_line_collection=True)
plt.title('y(t) = f(t)*w(t)')

# Spetrum
plt.subplot(322)
F = np.fft.fft(f)
plt.stem(t,F,use_line_collection=True)
plt.title('spectrum of f(t)')
plt.subplot(324)
W = np.fft.fft(w)
plt.stem(t,W,use_line_collection=True)
plt.title('Spectrum of w(t)')
plt.subplot(326)
Y = np.fft.fft(y)
# plt.stem(t,Y,use_line_collection=True)
plt.plot(t,Y)
plt.title('Spectrum of y(t)')
plt.tight_layout()

加窗后频谱

plt.figure(figsize=(6,6))
# 原信号f(t)
plt.subplot(3,1,1)
fs = 400 #采样频率
T = 0.04*2 #周期数目
N = fs*T #采样点数
t = np.arange(0,T,1/fs)
f = np.cos(200*np.pi*t)
t2 = np.arange(T,0.64,1/fs)
t = np.append(t,t2)
f = np.append(f,np.zeros(len(t2))) #补0增大频谱密度
plt.plot(t,f)
plt.title('$f(t) = cos(200 pi t))$')

plt.subplot(312)
F = np.fft.fft(f)
plt.plot(t,F)
plt.title('Spectrum')

plt.subplot(313)
plt.semilogy(t,abs(F))
# Z = 20*np.log10(abs(F))
# plt.plot(t,Z)
plt.ylim([0.001,100])
plt.title('Spectrum in semilogy')
plt.xlabel('Frequency(Hz)')
plt.ylabel('Aplitude(dB)')
plt.tight_layout()

差别不大的主瓣和旁瓣

(w_hnn(n）=0.5-0.5cos(frac{2pi n}{N-1}), n=0, 1, 2, cdots, N-1)
汉宁窗主瓣宽度增大，旁瓣高度减小；即牺牲分辨率，换来旁瓣泄露的减小

# hanning window
plt.subplot(211)
N = 256
y1 = np.hanning(32)
y2 = np.zeros(int(N-32))
y = np.append(y1,y2)
n = np.arange(0,N,1)
plt.stem(n,y,use_line_collection=True)
plt.title('hanning window')
# Spectrum
plt.subplot(212)
Y = np.fft.fft(y)
# plt.stem(n,abs(Y)/abs(len(Y)),use_line_collection=True)
# plt.plot(n,abs(Y)/max(abs(Y)))
plt.semilogy(n,abs(Y)/max(abs(Y)))
plt.tight_layout()

hanning window

(w_{hmm}(n)=0.54-0.46cos(frac{2pi n}{N-1}), n=0, 1, 2, cdots, N-1)
汉明窗相对矩形窗主瓣宽度增大，旁瓣高度减小；即牺牲分辨率，换来旁瓣泄露的减小。相对汉宁窗旁瓣高度减小不明显，衰减到最大幅度的8%左右而不是衰减至零，Blackman窗则主瓣更大，旁边更小。

# 窗函数对比
N = 4096
n = 32
y1a = np.ones(n)
y1b = np.hanning(n)
y1c = np.hamming(n)
y1d = np.blackman(n)
y2 = np.zeros(N-n)
n = np.arange(0,N,1)
# d = {'a':'rectangle', 'b':'hanning', 'c':'hamming', 'd':'blackman'}
d = ['rectangle', 'hanning', 'hamming', 'blackman']
count = 0

for y in [y1a,y1b,y1c,y1d]:
    yx = np.append(y,y2)
    Yx = np.fft.fft(yx)
    plt.semilogy(n,abs(Yx)/max(abs(Yx)),label=d[count])
    count+=1
    
plt.ylim(0.000001,1)
plt.xlim(0,N/2)
plt.legend(loc='upper right')
plt.yticks([1,0.1,0.01,0.001,0.0001,0.00001,0.000001],['0','-20','-40','-60','-80','-100','-120'])
plt.ylabel('Aplitude(dB)')
plt.title('窗函数比较',fontproperties='stsong')

窗函数比较

plt.figure(figsize=(12,6))
# 原信号f(t)
plt.subplot(231)
fs = 400 #采样频率
T = 0.04*4 #周期数目
N = 256 #采样点数
t = np.arange(0,T,1/fs)
f = np.cos(200*np.pi*t)+np.sin(100*np.pi*t)+np.cos(50*np.pi*t)
N0 = int(N - T*fs)
ft = np.append(f,np.zeros(N0))
t = np.arange(0,fs,fs/N)
plt.plot(t,ft,color='r')
plt.title('$f(t) = cos(200 pi t)+sin(100 pi t)+cos(50 pi t)$')
# add rectangle window
plt.subplot(234)
X = np.fft.fft(ft)
plt.plot(t,abs(X),label='rectangle')
plt.title('Retangle window Spectrum')

# add hamming window
plt.subplot(232)
x1c = np.hamming(T*fs)
ft = f*x1c
ft = np.append(ft,np.zeros(N0))
plt.plot(t,ft)
plt.title('$f(t)=f(t)*hamming(T*fs)$')
plt.subplot(235)
Xc = np.fft.fft(ft)
plt.plot(t,Xc)
plt.title('Hamming Window Spectrum')

# add blackman window
plt.subplot(233)
x1d = np.blackman(T*fs)
ft = f*x1d
ft = np.append(ft,np.zeros(N0))
plt.plot(t,ft)
plt.title('$f(t)=f(t)*blackman(T*fs)$')
plt.subplot(236)
Xd = np.fft.fft(ft)
plt.plot(t,Xd)
plt.title('blackman Window Spectrum')
plt.tight_layout()

窗函数比较

照惯例附上Github仓库对应代码链接

【推广】 免费学中医，健康全家人
原文地址：https://www.cnblogs.com/WindyZ/p/FFT_Analysis.html