什么是二分图:
二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。
一个二分图中的最大匹配数等于这个图中的最小点覆盖数
König定理是一个二分图中很重要的定理,它的意思是,一个二分图中的最大匹配数等于这个图中的最小点覆盖数。如果你还不知道什么是最小点覆盖,我也在这里说一下:假如选了一个点就相当于覆盖了以它为端点的所有边,你需要选择最少的点来覆盖所有的边。
题目:
有N台计算机和k个任务,我们可以给每台计算机分配一个任务,每台计算机能够处理的任务种类各不相同,请求出最多能够处理任务的个数;
二分图也可以这样理解:根据题目来。转化成图论模型分析,可以定义无向二分图G(U&&V,E)。
U代表计算机的顶点集合,V代表任务集合,对于任意的u属于U和v属于V,计算机u能够处理任务v《--》(u,v)属于E。
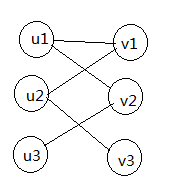
图一二分图的例子
注:图一为无向图
找了bin神的模板(套用下嘿嘿.!)
二分图模板: 模板一:匈牙利算法 /* ************************************************************************** //二分图匹配(匈牙利算法的DFS实现) //初始化:g[][]两边顶点的划分情况 //建立g[i][j]表示i->j的有向边就可以了,是左边向右边的匹配 //g没有边相连则初始化为0 //uN是匹配左边的顶点数,vN是匹配右边的顶点数 //调用:res=hungary();输出最大匹配数 //优点:适用于稠密图,DFS找增广路,实现简洁易于理解 //时间复杂度:O(VE) int g[MAXN][MAXN];//编号是0~n-1的 int linker[MAXN];//表示b集合中的i匹配到a集合的元素 //a集合代表毕业生b集合高校具体情况具体分析 bool used[MAXN];//b集合是否被访问 //***************************************************************************/ //顶点编号从0开始的 const int MAXN=510; int uN,vN;//u,v数目 int g[MAXN][MAXN]; int linker[MAXN]; bool used[MAXN]; bool dfs(int u)//从左边开始找增广路径 { int v; for(v=0;v<vN;v++)//这个顶点编号从0开始,若要从1开始需要修改 if(g[u][v]&&!used[v]) { used[v]=true; if(linker[v]==-1||dfs(linker[v])) {//找增广路,反向 linker[v]=u; return true; } } return false;//这个不要忘了,经常忘记这句 } int hungary() { int res=0; int u; memset(linker,-1,sizeof(linker)); for(u=0;u<uN;u++) { memset(used,0,sizeof(used)); if(dfs(u)) res++; } return res; }
实际上,可以将二分图最大匹配问题看成最大流问题(明天在补上这块知识,昨天就像写了)的一种特殊情况。不放对下图作如下变形。
将原图中的所有无向边e改成又向边,方向从U到V,容量为1.增加源点s和汇点t,从s向所有的顶点u属于U连一条容量为1的边,从所有顶点v属于V向t连一条容量为1的边。
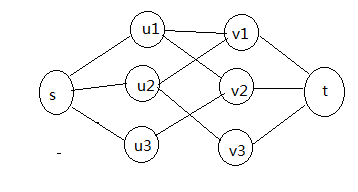
图二
注:图二为有向图并且权值为1;