二分图匹配

一、二分图最大匹配

　　Edmonds于1965年提出了匈牙利算法，解决了求取二分图最大匹配的问题。其算法思想是将初始匹配通过迭代寻找增广路径得到最大匹配，每次迭代得到的匹配大小加1。

　　增广路径的表现形式是一条“交错路径”，第一条边是目前没有参与匹配的，第二条参与匹配，第四条边没有参与......最后一条边没有参与匹配，并且始点和终点还没有被选过。那么对于这样一条路径，我们可以将第一条边改为已匹配，第二条边改为未匹配...以此类推。也就是将所有的边进行"反色"，容易发现这样修改以后，匹配仍然是合法的，但是匹配数增加了一对。另外，单独的一条连接两个未匹配点的边显然也是交错路径。可以证明。当不能再找到增广路径时，就得到了一个最大匹配，这也就是匈牙利算法的思路。

　　※几个重要结论：

　　1. 最小路径覆盖 = |V| - 最大匹配数

　　用尽量少的不相交简单路径覆盖有向无环图Ｇ的所有结点。解决此类问题可以建立一个二分图模型。把所有顶点i拆成两个：Ｘ结点集中的i和Y结点集中的i'，如果有边i->j，则在二分图中引入边i->j'，设二分图最大匹配为m，则结果就是|V|-m。

　　2. 最大独立集 = |V| - 最大匹配数

　　一个最大的点集，集合中任两个结点不相邻。最大独立集就是其补图的最大团。

　　3. 最小边覆盖 = |V| - 最大匹配数

　　边覆盖集即一个边集，使得所有点都与集合里的边邻接。或者说是“边” 覆盖了所有“点”。

　　4. 最小点覆盖 = 最大匹配数

　　用最少的点（Ｘ集合或Ｙ集合的都行）让每条边都至少和其中一个点关联。

　　※二分图最大匹配的König定理

　　König定理是一个二分图中很重要的定理，它的意思是，一个二分图中的最大匹配数等于这个图中的最小点覆盖数。

　　以下转自（http://www.matrix67.com/blog/archives/116）

　　假如我们已经通过匈牙利算法求出了最大匹配（假设它等于M），下面给出的方法可以告诉我们，选哪M个点可以覆盖所有的边。

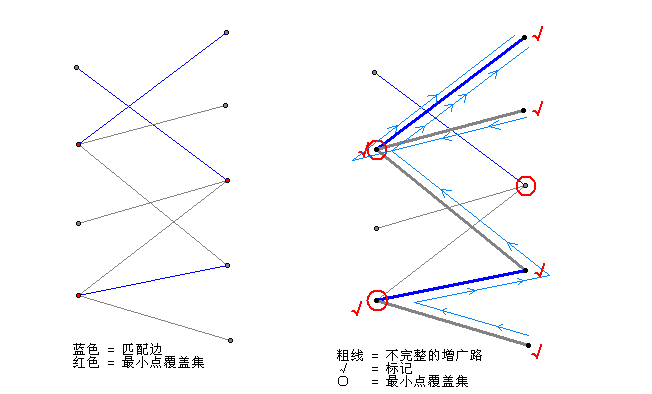
　　匈牙利算法需要我们从右边的某个没有匹配的点，走出一条使得“一条没被匹配、一条已经匹配过，再下一条又没匹配这样交替地出现”的路（交错轨，增广路）。但是，现在我们已经找到了最大匹配，已经不存在这样的路了。换句话说，我们能寻找到很多可能的增广路，但最后都以找不到“终点是还没有匹配过的点”而失败。我们给所有这样的点打上记号：从右边的所有没有匹配过的点出发，按照增广路的“交替出现”的要求可以走到的所有点（最后走出的路径是很多条不完整的增广路）。那么这些点组成了最小覆盖点集：右边所有没有打上记号的点，加上左边已经有记号的点。看图，右图中展示了两条这样的路径，标记了一共6个点（用 “√”表示）。那么，用红色圈起来的三个点就是我们的最小覆盖点集。
    首先，为什么这样得到的点集点的个数恰好有M个呢？答案很简单，因为每个点都是某个匹配边的其中一个端点。如果右边的哪个点是没有匹配过的，那么它早就当成起点被标记了；如果左边的哪个点是没有匹配过的，那就走不到它那里去（否则就找到了一条完整的增广路）。而一个匹配边又不可能左端点是标记了的，同时右端点是没标记的（不然的话右边的点就可以经过这条边到达了）。因此，最后我们圈起来的点与匹配边一一对应。
    其次，为什么这样得到的点集可以覆盖所有的边呢？答案同样简单。不可能存在某一条边，它的左端点是没有标记的，而右端点是有标记的。原因如下：如果这条边不属于我们的匹配边，那么左端点就可以通过这条边到达（从而得到标记）；如果这条边属于我们的匹配边，那么右端点不可能是一条路径的起点，于是它的标记只能是从这条边的左端点过来的（想想匹配的定义），左端点就应该有标记。
    最后，为什么这是最小的点覆盖集呢？这当然是最小的，不可能有比M还小的点覆盖集了，因为要覆盖这M条匹配边至少就需要M个点（再次回到匹配的定义）。

　　匈牙利模板：

 1 const int INF = 1<<29;
 2 const double eps = 1e-7;
 3 
 4 int nx,ny;
 5 int vis[N],linker[N];
 6 vector<int>G[N];
 7 
 8 bool find_path(int x)
 9 {
10     int sz = G[x].size();
11     for(int i=0; i<sz; i++) {
12         int v = G[x][i];
13         if(vis[v]) continue;
14         vis[v] = 1;
15         if(linker[v]==-1 || find_path(linker[v])) {
16             linker[v] = x; return true;
17         }
18     }
19     return false;
20 }
21 
22 int maxmatch()
23 {
24     int ret = 0;
25     memset(linker,-1,sizeof(linker));
26     for(int i=1; i<=nx; i++)
27     {
28         memset(vis,0,sizeof(vis));
29         if(find_path(i)) ret++;
30     }
31     return ret;
32 }

View Code

　　例题：hdu-2063

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<vector>
 4 #include<cstring>
 5 using namespace std;
 6 const int N = 510;
 7 
 8 const int INF = 1<<29;
 9 const double eps = 1e-7;
10 
11 int nx,ny;
12 int vis[N],linker[N];
13 vector<int>G[N];
14 
15 bool find_path(int x)
16 {
17     int sz = G[x].size();
18     for(int i=0; i<sz; i++) {
19         int v = G[x][i];
20         if(vis[v]) continue;
21         vis[v] = 1;
22         if(linker[v]==-1 || find_path(linker[v])) {
23             linker[v] = x; return true;
24         }
25     }
26     return false;
27 }
28 
29 int maxmatch()
30 {
31     int ret = 0;
32     memset(linker,-1,sizeof(linker));
33     for(int i=1; i<=nx; i++)
34     {
35         memset(vis,0,sizeof(vis));
36         if(find_path(i)) ret++;
37     }
38     return ret;
39 }
40 int main()
41 {
42     int i,j,k,m,n;
43     while(scanf("%d %d %d",&k,&n,&m)==3) {
44         for(i=1; i<=n; i++) G[i].clear();
45         nx = n, ny = m;
46         while(k--) {
47             scanf("%d %d",&i,&j);
48             G[i].push_back(j);
49         }
50         printf("%d
",maxmatch());
51     }
52     return 0;
53 }

View Code

　　时间复杂度的优化：Hopcroft-Karp算法

Hopcroft-Karp算法

　　该算法由John.E.Hopcroft和Richard M.Karp于1973提出，故称Hopcroft-Karp算法。

原理

　　为了降低时间复杂度，可以在增广匹配集合M时，每次寻找多条增广路径。这样就可以进一步降低时间复杂度，可以证明，算法的时间复杂度可以到达O（n^0.5*m），虽然优化不了多少，但在实际应用时，效果还是很明显的。

基本算法

　　该算法主要是对匈牙利算法的优化，在寻找增广路径的时候同时寻找多条不相交的增广路径，形成极大增广路径集，然后对极大增广路径集进行增广。在寻找增广路径集的每个阶段，找到的增广路径集都具有相同的长度，且随着算法的进行，增广路径的长度不断的扩大。可以证明，最多增广n^0.5次就可以得到最大匹配。

上题代码：

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<vector>
  4 #include<queue>
  5 #include<cstring>
  6 using namespace std;
  7 const int N = 510;
  8 const int INF = 0x3f3f3f3f;
  9 const double eps = 1e-7;
 10 int nx,ny;
 11 char vis[N];
 12 vector<int>G[N];
 13 
 14 int first[N], xlink[N], ylink[N];
 15 void init()
 16 {
 17     memset(first, -1, sizeof(first));
 18     memset(xlink, -1, sizeof(xlink));
 19     memset(ylink, -1, sizeof(ylink));
 20 }
 21 
 22 int dx[N], dy[N];
 23 int dis;
 24 
 25 int bfs()
 26 {
 27     queue<int> q;
 28     dis = INF;
 29     memset(dx, -1, sizeof(dx));
 30     memset(dy, -1, sizeof(dy));
 31     for(int i = 1; i <= nx; i++)
 32     {
 33         if(xlink[i] == -1)
 34         {
 35             q.push(i);
 36             dx[i] = 0;
 37         }
 38     }
 39     while(!q.empty())
 40     {
 41         int u = q.front(); q.pop();
 42         if(dx[u] > dis) break;
 43         for(int i=0; i<G[u].size(); i++)
 44         {
 45             int v = G[u][i];
 46             if(dy[v] == -1)
 47             {
 48                 dy[v] = dx[u] + 1;
 49                 if(ylink[v] == -1) dis = dy[v];
 50                 else
 51                 {
 52                     dx[ylink[v]] = dy[v]+1;
 53                     q.push(ylink[v]);
 54                 }
 55             }
 56         }
 57     }
 58     return dis != INF;
 59 }
 60 
 61 int Find(int u)
 62 {
 63     for(int i=0; i<G[u].size(); i++)
 64     {
 65         int v = G[u][i];
 66         if(!vis[v] && dy[v] == dx[u]+1)
 67         {
 68             vis[v] = 1;
 69             if(ylink[v] != -1 && dy[v] == dis) continue;
 70             if(ylink[v] == -1 || Find(ylink[v]))
 71             {
 72                 xlink[u] = v, ylink[v] = u;
 73                 return 1;
 74             }
 75         }
 76     }
 77     return 0;
 78 }
 79 
 80 int MaxMatch()
 81 {
 82     int ans = 0;
 83     while(bfs())
 84     {
 85         memset(vis, 0, sizeof(vis));
 86         for(int i = 1; i <= nx; i++)
 87             if(xlink[i] == -1)
 88                 ans += Find(i);
 89     }
 90     return ans;
 91 }
 92 
 93 int main()
 94 {
 95     int i,j,k,m,n;
 96     while(scanf("%d %d %d",&k,&n,&m)==3) {
 97         for(i=1; i<=n; i++) G[i].clear();
 98         init();
 99         nx = n, ny = m;
100         while(k--) {
101             scanf("%d %d",&i,&j);
102             G[i].push_back(j);
103         }
104         printf("%d
",MaxMatch());
105     }
106     return 0;
107 }

View Code

二、二分图最优匹配

【最优完备匹配】

　　对于二分图的每条边都有一个权（非负），要求一种完备匹配方案，使得所有匹配边的权和最大，记做最优完备匹配。（特殊的，当所有边的权为1时，就是最大完备匹配问题）

　　KM算法：（全称是Kuhn-Munkras，是这两个人在1957年提出的，有趣的是，匈牙利算法是在1965年提出的）

　　为每个点设立一个顶标L_i，先不要去管它的意义。设v_i,j为(i,j)边的权，如果可以求得一个完备匹配，使得每条匹配边v_i,j=L_i+L_j，其余边v_i,j≤L_i+L_j。此时的解就是最优的，因为匹配边的权和=∑L_i，其余任意解的权和都不可能比这个大

　　定理：二分图中所有v_i,j=L_i+L_j的边构成一个子图G，用匈牙利算法求G中的最大匹配，如果该匹配是完备匹配，则是最优完备匹配。

　　问题是，现在连L_i的意义还不清楚。

　　其实，我们现在要求的就是L的值，使得在该L值下达到最优完备匹配。

　　L初始化：

　　　　L_i=max{w_i,j}(i∈x,j∈y)

　　　　L_j=0

　　建立子图G，用匈牙利算法求G的最大匹配，如果在某点i (i∈x)找不到增广轨，则得不到完备匹配。

　　此时需要对L做一些调整：

　　　　设S为寻找从i出发的增广轨时访问的x中的点的集合，T为访问的y中的点的集合。

　　　　找到一个改进量dx，dx=min{L_i+L_j-w_i,j}(i∈S,j不∈T)

　　　　L_i=L_i-dx (i∈S)

　　　　L_i=L_i+dx (i∈T)

　　重复以上过程，不断的调整L，直到求出完备匹配为止。

　　从调整过程中可以看出：

　　　　每次调整后新子图中在包含原子图中所有的边的基础上添加了一些新边。

　　　　每次调整后∑L_i会减少dx，由于每次dx取最小，所以保证了解的最优性。

　　复杂度分析：

　　设n为点数，m为边数，从每个点出发寻找增广轨的复杂度是O(m)，如果找不到增广轨，对L做调整的复杂度也是O(m)，而一次调整或者找到一条增广轨，或者将两个连通分量合成一个，而这两种情况最多都只进行O(n)次，所以总的复杂度是O(nm)

　　扩展：根据KM算法的实质，可以求出使得所有匹配边的权和最小的匹配方案。

　　L初始化：

　　　　L_i=min{w_i,j}(i∈x,j∈y)

　　　　L_j=0

　　　　dx=min{w_i,j-L_i-L_j}(i∈S,j不∈T)

　　　　L_i=L_i+dx (i∈S)

　　　　L_i=L_i-dx (i∈T)

【最优匹配】

　　与最优完备匹配很相似，但不必以完备匹配为前提。

　　只要对KM算法作一些修改就可以了：

　　将原图转换成完全二分图（m=|x||y|），添加原图中不存在的边，并且设该边的权值为0。

　　模板:

 1 const int INF = 1<<30;
 2 const int maxn = 310;
 3 int linker[maxn], visx[maxn], visy[maxn], w[maxn][maxn];
 4 int slack[maxn], lx[maxn], ly[maxn];
 5 int nx, ny;
 6 bool DFS(int x)
 7 {
 8     visx[x] = 1;
 9     for(int y=1; y<=ny; y++)
10     {
11         if(visy[y]) continue;
12         int tmp = lx[x] + ly[y] - w[x][y];
13         if(!tmp)
14         {
15             visy[y] = 1;
16             if(linker[y] == -1 || DFS(linker[y]))
17             {
18                 linker[y] = x; return true;
19             }
20         }
21         else slack[y] = min(slack[y], tmp);
22     }
23     return false;
24 }
25 int KM()
26 {
27     int i,j;
28     memset(ly,0,sizeof(ly));
29     memset(linker,-1,sizeof(linker));
30     for(i=1; i<=nx; i++)
31         for(lx[i]=-INF,j=1; j<=ny; j++)
32             lx[i] = max(lx[i],w[i][j]);
33     for(int x=1; x<=nx; x++)
34     {
35         for(i=1; i<=ny; i++) slack[i] = INF;
36         while(1)
37         {
38             memset(visx,0,sizeof(visx));
39             memset(visy,0,sizeof(visy));
40             if(DFS(x)) break;
41             int d = INF;
42             for(i=1; i<=ny; i++) if(!visy[i]) d = min(d,slack[i]);
43             for(i=1; i<=nx; i++) if(visx[i]) lx[i]-=d;
44             for(i=1; i<=ny; i++)
45                 visy[i] ? ly[i]+=d : slack[i]-=d;
46         }
47     }
48     int ans = 0;
49     for(i=1; i<=nx; i++) if(linker[i]!=-1) ans+=w[linker[i]][i];
50     return ans;
51 }

View Code

例题：hdu2255

 1 #include<iostream>
 2 #include<cstring>
 3 #include<cstdio>
 4 #include<cmath>
 5 using namespace std;
 6 const int INF = 1<<30;
 7 const int maxn = 310;
 8 int linker[maxn], visx[maxn], visy[maxn], w[maxn][maxn];
 9 int slack[maxn], lx[maxn], ly[maxn];
10 int nx, ny;
11 bool DFS(int x)
12 {
13     visx[x] = 1;
14     for(int y=1; y<=ny; y++)
15     {
16         if(visy[y]) continue;
17         int tmp = lx[x] + ly[y] - w[x][y];
18         if(!tmp)
19         {
20             visy[y] = 1;
21             if(linker[y] == -1 || DFS(linker[y]))
22             {
23                 linker[y] = x; return true;
24             }
25         }
26         else slack[y] = min(slack[y], tmp);
27     }
28     return false;
29 }
30 int KM()
31 {
32     int i,j;
33     memset(ly,0,sizeof(ly));
34     memset(linker,-1,sizeof(linker));
35     for(i=1; i<=nx; i++)
36         for(lx[i]=-INF,j=1; j<=ny; j++)
37             lx[i] = max(lx[i],w[i][j]);
38     for(int x=1; x<=nx; x++)
39     {
40         for(i=1; i<=ny; i++) slack[i] = INF;
41         while(1)
42         {
43             memset(visx,0,sizeof(visx));
44             memset(visy,0,sizeof(visy));
45             if(DFS(x)) break;
46             int d = INF;
47             for(i=1; i<=ny; i++) if(!visy[i]) d = min(d,slack[i]);
48             for(i=1; i<=nx; i++) if(visx[i]) lx[i]-=d;
49             for(i=1; i<=ny; i++)
50                 visy[i] ? ly[i]+=d : slack[i]-=d;
51         }
52     }
53     int ans = 0;
54     for(i=1; i<=nx; i++) if(linker[i]!=-1) ans+=w[linker[i]][i];
55     return ans;
56 }
57 int main()
58 {
59     int i,j,k,m,n;
60     while(scanf("%d",&n) == 1)
61     {
62         nx = ny = n;
63         for(i=1; i<=n; i++)
64         {
65             for(j=1; j<=n; j++)
66             {
67                 scanf("%d",&k);
68                 w[i][j] = k;
69             }
70         }
71         printf("%d
",KM());
72     }
73     return 0;
74 }

View Code

三、二分图多重匹配

　　在二分图最大匹配中，每个点（不管是X方点还是Y方点）最多只能和一条匹配边相关联，然而，我们经常遇到这种问题，即二分图匹配中一个点可以和多条匹配边相关联，但有上限，或者说，L_i表示点i最多可以和多少条匹配边相关联。

　　二分图多重匹配分为二分图多重最大匹配与二分图多重最优匹配两种，分别可以用最大流与最大费用最大流解决。

（1）二分图多重最大匹配：
在原图上建立源点S和汇点T，S向每个X方点连一条容量为该X方点L值的边，每个Y方点向T连一条容量为该Y方点L值的边，原来二分图中各边在新的网络中仍存在，容量为1（若该边可以使用多次则容量大于1），求该网络的最大流，就是该二分图多重最大匹配的值。

（2）二分图多重最优匹配：
在原图上建立源点S和汇点T，S向每个X方点连一条容量为该X方点L值、费用为0的边，每个Y方点向T连一条容量为该Y方点L值、费用为0的边，原来二分图中各边在新的网络中仍存在，容量为1（若该边可以使用多次则容量大于1），费用为该边的权值。求该网络的最大费用最大流，就是该二分图多重最优匹配的值。

练习一

练习二