1、建图:将有上下界的网络流图转化成普通的网络流图
首先建立附加源点ss和附加汇点tt
对于原图中的边x->y,若限制为[b,c],那么连边x->y,流量为c-b
对于原图中的某点i,记d(i)为流入这点的所有边的下界和减去流出这点的所有边的下界和
若d(i)>0,那么连边ss->i,流量为d(i)
若d(i)<0,那么连边i->tt,流量为-d(i)
2、求解
在新图上跑ss到tt的最大流,若新图满流那么一定存在一种可行流
此时,原图中每一条边的流量应为新图中对应的边的流量+这条边的流量下界
3、证明
在原图中,假设每条边的实际流量为f(u,v)=b(u,v)+g(u,v),其中g(u,v)≤c(u,v)−b(u,v)
我们可以将原图中的边改为上界为c(u,v)−b(u,v)的边,变成一个普通的网络流图
经以上改造,g(u,v)实际上是新图中边u->v的实际流量,原图中的实际流量f(u,v)=b(u,v)+g(u,v)
但是如果在这个新图中直接求可行流的话是错误的



原图,按上面方法改造的新图的可行流为1,还原成原图的实际流量并不满足平衡条件

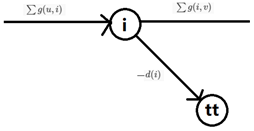
当d(i)>0d(i)>0时∑g(i,v)=∑g(u,i)+d(i) 当d(i)<0d(i)<0时∑g(u,i)=∑g(i,v)+[−d(i)]
需要一条边流量为d(i)d(i)来补流 需要一条边流量为−d(i)−d(i)来分流
易知:添加的所有与附加源点或者附加汇点相连的边必须满流,原图才有可行流,证毕!
https://vjudge.net/problem/SGU-194

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int maxn = 2e2+10; const int maxm = 2e5+10; const int inf = 0x3f3f3f3f; struct Edge{int u, v, nxt; ll w;}E[maxm+maxn*2]; int head[maxn], vis[maxn], cur[maxn], dis[maxn]; int node_num, S, T, n, m, cnt; ll balance[maxn]; ll low[maxm]; ll ans[maxm]; inline void add_edge(int u, int v, ll w) { E[cnt].w = w, E[cnt].v = v, E[cnt].nxt = head[u], head[u] = cnt++; E[cnt].w = 0, E[cnt].v = u, E[cnt].nxt = head[v], head[v] = cnt++; } inline bool BFS() { for (int i = 0; i <= node_num; ++ i) dis[i] = -1; dis[S] = 0; queue<int> q; q.push(S); while (!q.empty()) { int u = q.front(); q.pop(); for (int i = head[u]; ~i; i = E[i].nxt) { int v = E[i].v; if (dis[v] == -1 && E[i].w) dis[v] = dis[u]+1, q.push(v); } } return dis[T] != -1; } inline ll DFS(int u, ll flow) { if (u == T) return flow; ll del = flow; for (int i = cur[u]; ~i; i = E[i].nxt) { cur[u] = E[i].nxt; int v = E[i].v; if (dis[v] == dis[u] + 1 && E[i].w > 0) { ll ans = DFS(v, min(del, E[i].w)); E[i].w -= ans; E[i^1].w += ans; del -= ans; if (del == 0) break; } } return flow - del; } inline ll Dinic() { ll ans = 0; while (BFS()) { for (int i = 0; i <= node_num; ++ i) cur[i] = head[i]; ans += DFS(S, inf); } return ans; } int main() { while (~scanf("%d %d", &n, &m)) { cnt = 0; S = 0, T = n+1, node_num = T; memset(head, -1, sizeof(head)); memset(balance, 0, sizeof(balance)); for (int i = 1; i <= m; ++ i) { int u, v; ll L, R; scanf("%d %d %lld %lld", &u, &v, &low[i], &R); balance[u] -= low[i], balance[v] += low[i]; //发现进出减的都是low add_edge(u, v, R-low[i]); } ll flow_blc_sum = 0; int rec_edge_num = cnt-1; for (int i = 1; i <= n; ++ i) { if (balance[i] > 0) add_edge(S, i, balance[i]), flow_blc_sum += balance[i]; else if (balance[i] < 0) add_edge(i, T, -balance[i]); //这里需要注意有个负号 } if (Dinic() == flow_blc_sum) { cout << "YES" << endl; for (int i = 1; i <= m; ++ i) cout << E[(i-1)*2 ^ 1].w + low[i] << endl; //这里这么输出就行了, 就是残余网络的w加上low[i] //话说这个dinic好像是反边里面才是最大流的样子 } else cout << "NO" << endl; } return 0; }
二、有源汇可行流
1、建图
在原图中添加一条边t->s,流量限制为[0,inf],即让源点和汇点也满足流量平衡条件,这样就改造成了无源汇的网络流图,其余方法同上
2、求解 同无源汇可行流
3、证明 同无源汇可行流
三、有源汇最大流
1、建图 同有源汇可行流
2、求解
在新图上跑ss到tt的最大流,满流则存在可行流,记此时∑f(s,i)=sum1,
然后将t->s这条边拆掉,在新图上跑s到t最大流,记此时∑f(s,i)=sum2
最终答案即为sum1+sum2
3、证明
添加附加源汇的作用:为了满足流量平衡条件,在新图中进行相应的补流或分流
只要连接附加源汇的边满流,新图中s->t的任意一种可行流都是原图的可行流
跑ss->tt的最大流了之后,相当于是使连接附加源汇的边满流,进而求出了一种可行流
将t->s的边拆掉(使s->t变成一个有源汇的网络流图),跑s到t的最大流
加上跑出来的最大流即为原图中一种可行的最大流

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int maxn = 2e3+10; const int maxm = 2e5+10; const int inf = 0x3f3f3f3f; struct Edge{int u, v, nxt; int w;}E[maxm+maxn*2]; int head[maxn], vis[maxn], cur[maxn], dis[maxn]; int node_num, n, m, cnt, S, T; //fake S T, real S T int balance[maxn]; //int low[maxm]; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x*=10;x+=ch-'0';ch=getchar();} return x*f; } inline void add_edge(int u, int v, int w) { E[cnt].w = w, E[cnt].v = v, E[cnt].nxt = head[u], head[u] = cnt++; E[cnt].w = 0, E[cnt].v = u, E[cnt].nxt = head[v], head[v] = cnt++; } inline bool BFS(int S, int T) { for (int i = 0; i <= node_num; ++ i) dis[i] = -1; dis[S] = 0; queue<int> q; q.push(S); while (!q.empty()) { int u = q.front(); q.pop(); for (int i = head[u]; ~i; i = E[i].nxt) { int v = E[i].v; if (dis[v] == -1 && E[i].w) dis[v] = dis[u]+1, q.push(v); } } return dis[T] != -1; } int DFS(int u, int f, int T) { if (u == T) return f; int w, used = 0; for (int i = cur[u]; ~i; i = E[i].nxt) if (dis[E[i].v] == dis[u]+1) { w = f-used; w = DFS(E[i].v, min(E[i].w,w), T); E[i].w -= w; if (E[i].w) cur[u] = i; E[i^1].w += w, used += w; if (used == f) return f; } if (!used) dis[u] = 1; return used; } void dinic(int S,int T) { while(BFS(S,T)) { for(int i=0;i<=n+m+3;i++) cur[i]=head[i]; DFS(S,inf,T); } } bool judge() { int SS = T+1, TT = T+2; for (int i = 0; i <= T; i++) { if (balance[i] > 0) add_edge(SS, i, balance[i]); if (balance[i] < 0) add_edge(i, TT, -balance[i]); } dinic(SS, TT); for(int i = head[SS]; ~i; i = E[i].nxt) if (E[i].w) return 0; return 1; } int main() { while (~scanf("%d %d", &n, &m)) { cnt = 0; S = 0, T = n+m+1; node_num = T+2; memset(head, -1, sizeof(head)); memset(balance, 0, sizeof(balance)); for (int i = 1; i <= m; ++ i) { int low = read(); add_edge(n+i, T, inf-low); balance[n+i] -= low, balance[T] += low; } for (int i = 1; i <= n; ++ i) { int C = read(), D = read(); for (int j = 1; j <= C; ++ j) { int v = read(); int L = read(), R = read(); add_edge(i, n+v+1, R-L); balance[i] -= L, balance[n+v+1] += L; } add_edge(S, i, D); } add_edge(T, S, inf); int ans = 0; if (judge()) { dinic(S, T); add_edge(T, S, -inf); for (int i = head[S]; ~i; i = E[i].nxt) ans += E[i^1].w; printf("%d\n", ans); } else cout << "-1" << endl; cout << endl; } return 0; }
四、有源汇最小流
1、建图 同无源汇可行流
2、求解
求ss->tt最大流,连边t->s,inf,求ss->tt最大流,答案即为边t->s,inf的实际流量
3、证明
第一遍做的时候并无t->s这条边,所以s->t的流量已经尽力往其它边流了
加上t->s这条边后,流过这条边的都是些剩余的流不到其他边的流量,从而达到尽可能减少T->S这边上的流量的效果,即减小了最终答案。

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int maxn = 2e3+10; const int maxm = 2e5+10; const int inf = 0x3f3f3f3f; struct Edge{int u, v, nxt; int w;}E[maxm+maxn*2]; int head[maxn], vis[maxn], cur[maxn], dis[maxn]; int node_num, n, m, cnt, S, T; //fake S T, real S T int balance[maxn]; //int low[maxm]; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x*=10;x+=ch-'0';ch=getchar();} return x*f; } inline void add_edge(int u, int v, int w) { E[cnt].w = w, E[cnt].v = v, E[cnt].nxt = head[u], head[u] = cnt++; E[cnt].w = 0, E[cnt].v = u, E[cnt].nxt = head[v], head[v] = cnt++; } inline bool BFS(int S, int T) { for (int i = 0; i <= node_num; ++ i) dis[i] = -1; dis[S] = 0; queue<int> q; q.push(S); while (!q.empty()) { int u = q.front(); q.pop(); for (int i = head[u]; ~i; i = E[i].nxt) { int v = E[i].v; if (dis[v] == -1 && E[i].w) dis[v] = dis[u]+1, q.push(v); } } return dis[T] != -1; } int DFS(int u, int f, int T) { if (u == T) return f; int w, used = 0; for (int i = cur[u]; ~i; i = E[i].nxt) if (dis[E[i].v] == dis[u]+1) { w = f-used; w = DFS(E[i].v, min(E[i].w,w), T); E[i].w -= w; if (E[i].w) cur[u] = i; E[i^1].w += w, used += w; if (used == f) return f; } if (!used) dis[u] = 1; return used; } void dinic(int S,int T) { while(BFS(S,T)) { for(int i=0;i<=n+m+3;i++) cur[i]=head[i]; DFS(S,inf,T); } } //bool judge() { // int SS = T+1, TT = T+2; // for (int i = 0; i <= T; i++) { // if (balance[i] > 0) add_edge(SS, i, balance[i]); // if (balance[i] < 0) add_edge(i, TT, -balance[i]); // } // dinic(SS, TT); //// for(int i = head[SS]; ~i; i = E[i].nxt) //// if (E[i].w) return 0; //// return 1; //} int main() { scanf("%d", &n); cnt = 0; S = 0, T = n+1; node_num = T+2; memset(head, -1, sizeof(head)); memset(balance, 0, sizeof(balance)); for (int i = 1; i <= n; ++ i) { int num; scanf("%d", &num); while (num--) { int v; scanf("%d", &v); balance[i] -= 1, balance[v] += 1; add_edge(i, v, inf-1); } } for (int i = 1; i <= n; ++ i) add_edge(S, i, inf), add_edge(i, T, inf); int ans = 0; int SS = T+1, TT = T+2; for (int i = 0; i <= T; i++) { if (balance[i] > 0) add_edge(SS, i, balance[i]); if (balance[i] < 0) add_edge(i, TT, -balance[i]); } dinic(SS, TT); add_edge(T, S, inf); dinic(SS, TT); for(int i = head[T]; ~i; i = E[i].nxt) if (E[i].v == S) { cout << E[i^1].w << endl; break; } // return 1; //} // if (judge()) { // dinic(S, T); add_edge(T, S, -inf); // for (int i = head[S]; ~i; i = E[i].nxt) // ans += E[i^1].w; // printf("%d\n", ans); // } return 0; }
五、有源汇费用流
1、建图 将有上下界的网络流图转化成普通的网络流图
首先建立附加源点ss和附加汇点tt
对原图中某边x->y,若限制为[b,c],费用为cost,那么连边x->y,流量为c-b,费用为cost
对原图中某点i,记d(i)为流入这个点的所有边的下界和减去流出这个点的所有边的下界和
若d(i)>0,那么连边ss->i,流量为d(i),费用为0
若d(i)<0,那么连边i->tt,流量为-d(i),费用为0
连边t->s,流量为inf,费用为0
2、求解 跑ss->tt的最小费用最大流,答案即为(求出的费用+原图中边的下界*边的费用)
3、证明同 有源汇的可行流
4、注意:
有上下界的费用流指的是在满足流量限制条件和流量平衡条件的情况下满足流量限制条件和流量平衡条件的情况下的最小费用流,而不是在满足流量限制条件和流量平衡条件并且满足最大流的情况下的最小费用流——也就是说,有上下界的费用流只需要满足网络流的条件就可以了,而普通的费用流是满足一般条件并且满足是最大流的基础上的最小费用
个人小结:下面四段对应四个上下界网络流
开SS与TT,并且SS向图中的某些点连边,图中某些点向TT连边,能跑到SS到TT满流就是有可行解,因为每条边即有入点又有出点,所以SS和流出量与TT的流入量必定相等,此时原图中每一条边的流量应为新图中对应的边的流量+这条边的流量下界,总流量是SS流出流亦即TT流入量(注意不是流量下限和!)
连边T->S,下限为0,上限无穷,然后再同上开SS与TT,先跑SS到TT,满流表示有解,T到S边的流量就是此可行流的流量
连边T->S,下限为0,上限无穷,然后再同上开SS与TT,先跑SS到TT,满流表示有解,然后在满流的基础上面再跑!!!新图的CAP容量值是保留的,这时从S到T的流是新的增广路产生的流,就是说SUM2不包含SUM1,而SUM1是满足各边下限差额的一个可行流的流量,所以两者相加就是结果
开SS与TT,先跑SS到TT,满流表示有解,在此基础上连边T->S,下限为0,上限无穷,因为T到S的边的下限是0,所以对SS流出与TT流入量是没有影响的(从这里可以得到一个启发:网络流可以先跑,然后加边,再跑,再加边),然后再跑SS到TT,此时边T到S的流量就是最小流!
