本来是不打算写这个的,感觉不是一个大章节…然而看蓝书确实把我看懵逼了,想了一晚上都没想通原理。今天终于想明白了,所以整理一下。
直接来找公式的话请直接翻加粗字体,忽略废话。
定义
前置知识点:序列前缀和,差分序列,LCA
差分的用处以及原理迁移到树上进行转化。
实现及原理
《算法竞赛进阶指南》中引用了三道例题来解释原理以及用法。
但有一说一,可能我是个傻子,愣是差点变成了背公式。
先搬出来让我顿悟的一篇博客吧。大佬很强啊
其中诠释了把链分成两段的思想。那我想做的就是补两个图总结一下之类的。
众所周知,树上差分有两块难啃的骨头
关于边的差分
有了引入博客的拆链思想,我们可以把关于边的差分向最朴素的序列差分进行转换。
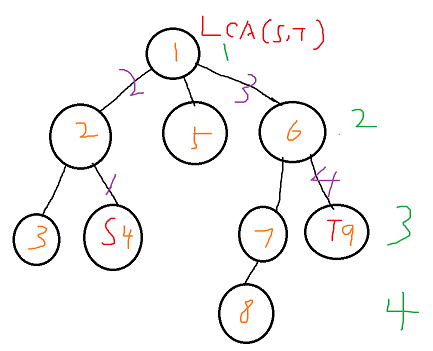
红色S代表起点,T代表重点。LCA已经明确标出。橙色的是点序号,绿色的深度,紫色是边的序号。
那么如果是S到T的所有边加上x。我们把链拆成两条。包括 Edge(1,2)和Edge(3,4)
根据朴素序列的差分,我们知道应在最左端加x,最右端的右移一位减x。但朴素的序列差分是一个一个点的形态,转换到边上,实际操作的时候就犯了个懵。其实我们不妨把点和边联合起来视作一个大点。
这里我们把点4和边1视作一个点。以此类推。然后就很自然的套入朴素序列差分,就有了公式:
令节点S的权值+x,令节点T的权值+x,令节点LCA(S,T)的权值-2*x
进行一次深度优先遍历。F[x]表示以x为根的子树种各节点的权值之和。F[x]就是x与他父亲之间的边被增加的值
关于点的差分
点应该就不需要什么特殊的思想了。单独分成两条链后,一条是包含了LCA点的,一条没有包含。所以理所当然Father(LCA)也会被牵扯进去。至于到底是哪条包含了,似乎是任意的。
直接放公式:
令节点S的权值+x,令节点T的权值+x,令节点LCA(S,T)的权值-x,令节点Father( LCA(S,T) )的权值-x