什么??你问我为什么不在一篇文章写完所有方法??
Hmm…其实我是想的,但是博皮的加载速度再带上文章超长图片超多的话…
可能这辈子都打不开了吧…
福特算法(Bellman-Ford)
适用范围及时间复杂度
单源最短路径算法,可处理负边权,但,无法处理负回路的情况。时间复杂度O(NE)
N:顶点数,E:边数
核心思想
松弛计算。什么是松弛计算?你戳…

……
好吧我说…
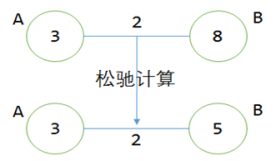 松弛计算之前,点B的值是8,但点A的值加上边上的权重2,得到点B的值是5,5<8,更新B为5。这个过程的意义是:找到了一条通向B更短的路线,且该路线先经过A,然后通过权重为2的边,到达点B。
松弛计算之前,点B的值是8,但点A的值加上边上的权重2,得到点B的值是5,5<8,更新B为5。这个过程的意义是:找到了一条通向B更短的路线,且该路线先经过A,然后通过权重为2的边,到达点B。
当然,也会存在另一种情况:
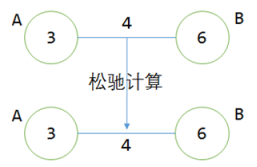 在进行松弛计算之前,点B的值是6,点A加上点边上的权值4得到7>6,表示没有找到通向B点更短的路线,故B不需要更新。
在进行松弛计算之前,点B的值是6,点A加上点边上的权值4得到7>6,表示没有找到通向B点更短的路线,故B不需要更新。
这也就诠释了为什么算法不可以处理负权回路的情况。
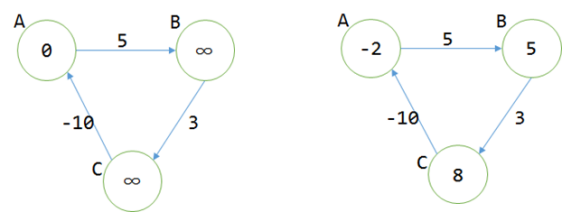
使用松弛之后,发现程序陷入死循环。
代码实现
不难发现,在使用算法前,我们要去检验负权回路。我们需要不断地迭代以求解。
初始化
首先我们需要一个边集数组,暂定u表示起点,v表示终点,w表示权。而这个数组的长度为边的数量。
顶点数*(顶点数-1)/2。
什么?你不知道什么是边集数组?
边集数组 边集数组是利用一维数组存储图中所有边的一种图的表示方法。 该数组中所存储的元素个数要大于等于图中所有的边数。 每个元素用来存储图一条边起点,终点和权值。 struct edge{int s,e;double w;}edges[maxn*(maxn-1)/2]; 特别注意的是:如果是无向图,则边的数量=顶点数量*(顶点数量-1)/2,加边函数为: void addEdges(int u,int v,double w){ edges[++idx].s=u;edges[idx].e=v;edges[idx].w=w; edges[++idx].e=u;edges[idx].s=v;edges[idx].w=w; } 而在枚举边的时候,需要枚举idx条边。 定义边集数组时,特别要注意取值范围 边集数组是针对边的,如果题目给定了边的数量为n ,那么在无向邻接矩阵中,边集数组要定义为2*n+1, 必须考虑来回。如果题目只给定了顶点数p,没有给定边数, 则边集数组的取值为:p*(p-1)/2
因为是无向图,算法第一层循环枚举点,第二层枚举边,所以加边函数的定义应是无向图的方法。
算法核心
void bellman(){ while(--n){ bool b=false; for(int j=1;j<=idx;j++){ if(dis[edges[j].e]>dis[edges[j].s]+edges[j].w){ dis[edges[j].e]=dis[edges[j].s]+edges[j].w; b=true; } } if(!b){ break; } } }
----------7.22 Update
学个A*不知道扒出来了我多少学错了的东西…这篇里面提到了最基本的福特算法,但是有一个队列优化没有补充。我一直误以为SPFA是福特算法的别称,在这里做出纠正顺便优化一下之前乱七八糟的写法。
SPFA(队列优化的Bellman-Ford)
仅仅在大陆流行叫这个优化SPFA。优化过后,在随机数据的表现情况为O(KE),K是一个较小的常数。在特殊构造中,有可能被退化成O(NE)。
优化思想是:
1.建立一个队列,最初队列中只有一个起点1
2.取出队首节点x,扫描他的所有出边(x,y,z)。如果有Dis[y]>Dis[x]+z,则用后者更新前者。同时,若y不在队列中,将y入队
3.重复以上步骤,直至队列为空。
这个队列避免了福特算法中对不需要进行扩展的节点的冗余扫描。
void spfa() { memset(Distance,0x3f,sizeof(Distance)); memset(Vist,0,sizeof(Vist)); Distance[1]=0; Vist[1]=1; q.push(1); while(q.size()) { int x=q.front(); q.pop(); Vist[x]=0; for(int i=head[x]; i; i=Edges[i].Next) { int y=Edges[i].End,z=Edges[i].Val; if(Distance[y]>Distance[x]+z) { Distance[y]=Distance[x]+z; if(!Vist[y]) { q.push(y),Vist[y]=1; } } } } }