这里是中等难度的网络流题集合。
IV.最长不下降子序列问题
本题介绍一种与符合一定长度限制的路径数量等相关的建模方式:分层建模。
看题目。第一问暴力dp就可以。二、三两问需要建图。
设最长不下降子序列的长度为\(s\),原数组为\(num\)。
则:
1.因为每个点只能在一条路径中,我们将它拆成两个点\(in_x\)与\(out_x\),在这两个点中间连一条边权为\(1\)的边。
2.因为是最长路径,则每个点\(x\)在路径中所处的位置是一定的(不然最长路径的长度还能增加),就是以\(x\)为结尾的\(LIS\)的长度(dp数组\(f\))。因此我们可以按\(LIS\)长度建出分层图。
对于\(f_x=1\)的点\(x\),连边\((S,in_x,1)\)。
对于\(f_x=s\)的点\(x\),连边\((out_x,T,1)\)。
同时,对于\(f_x=f_y+1,x>y,num_x\ge num_y\)的点对\((x,y)\),连边\((out_y,in_x,1)\)。
如图 (拆点没有表现出来):

可以看出,这张图里面每一条增广路,长度都是\(s\),且里面所有节点构成一条\(LIS\)。
则第二问的答案就是这张图的最大流。
第三问,就是取消关于\(1\)和\(n\)的流量限制(从\(S\)来的边,到\(T\)去的边,连接\(in\)和\(out\)间的边),再跑一遍最大流。
代码:
#include<bits/stdc++.h>
using namespace std;
int n,f[1010],num[1010],res,head[1010],S,T,cnt,cur[1010],dep[1010],mx;
struct node{
int to,next,val;
}edge[301000];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
int main(){
scanf("%d",&n),S=n*2+1,T=n*2+2;
for(int i=1;i<=n;i++)scanf("%d",&num[i]);
for(int i=1;i<=n;i++){
f[i]=1;
for(int j=1;j<i;j++)if(num[j]<=num[i])f[i]=max(f[i],f[j]+1);
mx=max(mx,f[i]);
}
printf("%d\n",mx);
memset(head,-1,sizeof(head)),cnt=res=0;
for(int i=1;i<=n;i++)ae(i,i+n,1);
for(int i=1;i<=n;i++){
if(f[i]==1)ae(S,i,1);
if(f[i]==mx)ae(i+n,T,1);
for(int j=1;j<i;j++)if(num[j]<=num[i]&&f[i]==f[j]+1)ae(j+n,i,1);
}
Dinic();
printf("%d\n",res);
ae(1,n+1,0x10000000),ae(S,1,0x10000000),ae(n,n+n,0x10000000);
if(f[n]==mx)ae(n+n,T,0x10000000);
Dinic();
printf("%d\n",res);
return 0;
}
X.餐巾计划问题
费用流太毒瘤了QaQ
关于这道题,我们还是采取暴力建图的措施,用最大流保证合法性,用最小费用保证最优性。
对于每一天,我们都拆成两个点:\(day\)表示早晨,\(eve\)表示夜晚。设一张新餐巾的费用为\(new\),快洗时间为\(t1\),费用为\(c1\);慢洗时间为\(t2\),费用为\(c2\)。每天需要\(need_i\)块餐巾。
则在\(day_i\)储存的流量,都是干净餐巾;在\(eve_i\)储存的流量,都是脏餐巾。
1.对于每个\(i\),连一条边\((S,day_i,INF,new)\),表示每天早晨可以购买无限条费用为\(new\)的干净餐巾。
2.对于每个\(i\),连一条边\((day_i,T,need_i,0)\),表示每天需要交出\(need_i\)块干净餐巾。交餐巾不需要费用。
3.对于每个\(i\),连一条边\((S,eve_i,need_i,0)\),表示每天晚上会产生\(need_i\)条脏餐巾。(注意是从\(S\)连来而不是从\(day_i\)连来,\(day_i\)的流量是直接连到\(T\)的。这相当于吃掉\(need_i\)条干净餐巾,再给你吐出来\(need_i\)条脏餐巾。因此不能直接连\((day_i,eve_i)\)。)
4.对于每个\(i\),连一条边\((eve_i,eve_{i+1},INF,0)\),表示每天晚上可以剩任意多条脏餐巾给第二天。剩餐巾也不需要费用。
5.对于每个\(i\),连一条边\((eve_i,day_{i+t1},INF,c1)\),表示每天晚上可以送任意多条脏餐巾给快洗部。快洗部会在\(c1\)天后的早晨送来等量的干净餐巾。这种操作每次需要\(c1\)的费用。
6.对于每个\(i\),连一条边\((eve_i,day_{i+t2},INF,c2)\),表示每天晚上可以送任意多条脏餐巾给慢洗部。快洗部会在\(c2\)天后的早晨送来等量的干净餐巾。这种操作每次需要\(c2\)的费用。
之后跑出来的最小费用即为答案。
由于建图太形象了,相信你一遍就可以感性理解
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,head[5010],S,T,need[5010],nw,t1,t2,c1,c2,cost,dis[5010],cnt,fr[5010],id[5010];
struct node{
int to,next,val,cost;
}edge[101000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[5010];
bool SPFA(){
memset(dis,0x3f3f3f3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x3f3f3f3f3f3f3f3f)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
signed main(){
scanf("%lld",&n),memset(head,-1,sizeof(head)),S=2*n+1,T=2*n+2;
for(int i=1;i<=n;i++){
scanf("%lld",&need[i]);
ae(i,T,need[i],0);
if(i+1<=n)ae(i+n,i+1+n,0x3f3f3f3f,0);
ae(S,i+n,need[i],0);
}
scanf("%lld%lld%lld%lld%lld",&nw,&t1,&c1,&t2,&c2);
for(int i=1;i<=n;i++){
ae(S,i,0x3f3f3f3f,nw);
if(i+t1<=n)ae(i+n,i+t1,0x3f3f3f3f,c1);
if(i+t2<=n)ae(i+n,i+t2,0x3f3f3f3f,c2);
}
while(SPFA());
printf("%lld\n",cost);
return 0;
}
XII.太空飞行计划问题
我还是太蒻了,一碰到“费用”这种东西就被带偏了,光想着怎么建费用流,虽然思路基本正确,但是本题是无法用费用流解决的。
首先,同[NOI2009]植物大战僵尸一样,我们可以建出图来,从源点向每个器材连(价格)单位的边,从每场实验向汇点连(收益)单位的边,再从每个器材向所有需要它的实验连\(INF\)单位的边,之后跑最小割,答案即为(收益和-最小割)。
关于为什么答案是(收益和-最小割),以及为什么要这么连边,在[NOI2009]植物大战僵尸中我们已经证明过了。现在我们关注的是求一种具体方案的过程。
首先,一个器材如果在源点处被割掉,那说明它是应该选的,在总收益中直接减去它的费用这种方案比在汇点处割掉它要更优。因此,如果在\(Dinic\)的最后一遍bfs分层中,这个器材没有被分上层(从源点到不了),就说明它在源点处被割掉了,它应该被选择。
然后,对于一场实验,如果它在汇点处被割掉,那么说明它不应该被选,选择它的耗费是大于收益的。因此,如果在最后一遍分层中,这个器材被分上层了,就说明它没有在汇点被割掉,不应该被选择。
最终方案就是,遍历所有的器材和实验,如果它没有被分层,则选择它。
附:或许是我太蒻了,题目中给出的读入代码我套进代码就出锅了,我不得不魔改了一番
代码:
#include<bits/stdc++.h>
using namespace std;
int m,n,head[210],cnt,S,T,cur[210],dep[210],res,sum;
struct node{
int to,next,val;
}edge[400100];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
void read(int i){
char tools[10000];
memset(tools,0,sizeof tools);
cin.getline(tools,10000);
int ulen=0,tool;
while (sscanf(tools+ulen,"%d",&tool)==1)
{
ae(tool,i,0x3f3f3f3f);
while(tool)tool/=10,ulen++;
ulen++;
}
ulen++;
}
int main(){
scanf("%d%d",&m,&n),memset(head,-1,sizeof(head)),S=n+m+1,T=n+m+2;
for(int i=1,x;i<=m;i++){
scanf("%d",&x),sum+=x;
ae(i+n,T,x);
read(i+n);
}
for(int i=1,x;i<=n;i++)scanf("%d",&x),ae(S,i,x);
Dinic();
for(int i=n+1;i<=n+m;i++)if(!dep[i])printf("%d ",i-n);puts("");
for(int i=1;i<=n;i++)if(!dep[i])printf("%d ",i);puts("");
printf("%d\n",sum-res);
return 0;
}
XXIII.最长k可重线段集问题
几乎和上一题完全一致。唯一的区别是,可能出现线段垂直于\(x\)轴的情况。也就是说,起点和终点的\(x\)坐标相同。而在上一题中是不可能出现这种状况的。
怎么办呢?
我想了一个非常繁琐的方法:把线段从开线段转成闭线段再转回来。
首先,把每个\(x\)坐标都乘二,然后除非左右坐标重合,将左坐标加一,将右坐标减一。
s[i].x*=2,t[i].x*=2;
if(s[i].x==t[i].x)r[i]=make_pair(s[i].x,t[i].x);
else r[i]=make_pair(s[i].x+1,t[i].x-1);
然后把它离散化。这就完成了开线段转闭线段的工作。
最后再把每个\(x\)坐标再乘二,然后左坐标减一,右坐标加一。
然后再离散化。这就完成了闭线段转开线段的工作。
然后方法就一样了。
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int,int>
#define x first
#define y second
#define mp make_pair
int n,k,S,T,len[510],lim,dis[2010],fr[2010],id[2010],cost,cnt,head[2010];
pii s[510],t[510],r[510];
vector<int>v;
struct node{
int to,next,val,cost;
}edge[101000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[2100];
bool SPFA(){
memset(dis,-1,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]<dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==-1)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=mn*dis[T],x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
signed main(){
scanf("%lld%lld",&n,&k),memset(head,-1,sizeof(head));
for(int i=1;i<=n;i++){
scanf("%lld%lld%lld%lld",&s[i].x,&s[i].y,&t[i].x,&t[i].y);
if(s[i]>t[i])swap(s[i],t[i]);
len[i]=(int)sqrt((s[i].x-t[i].x)*(s[i].x-t[i].x)+(s[i].y-t[i].y)*(s[i].y-t[i].y));
s[i].x*=2,t[i].x*=2;
if(s[i].x==t[i].x)r[i]=make_pair(s[i].x,t[i].x);
else r[i]=make_pair(s[i].x+1,t[i].x-1);
v.push_back(r[i].x),v.push_back(r[i].y);
}
sort(v.begin(),v.end()),v.resize(unique(v.begin(),v.end())-v.begin()),lim=v.size(),S=lim*2+2,T=lim*2+3;
for(int i=1;i<=lim*2;i++)ae(i,i+1,k,0);
ae(S,1,k,0),ae(lim*2+1,T,k,0);
for(int i=1;i<=n;i++)r[i].x=lower_bound(v.begin(),v.end(),r[i].x)-v.begin()+1,r[i].y=lower_bound(v.begin(),v.end(),r[i].y)-v.begin()+1,ae(r[i].x*2-1,r[i].y*2+1,1,len[i]);
// for(int i=1;i<=n;i++)printf("(%lld,%lld):%lld\n",r[i].x,r[i].y,len[i]);
while(SPFA());
printf("%d\n",cost);
return 0;
}
XXIV.汽车加油行驶问题
在A掉这道题之前,我曾经与它见过2遍。第1次还不会网络流,懵了一会后果断放弃。第2次会了网络流,又懵了一会后再次放弃。直到今天……
还是懵了,看了题解。
在这道题中,我们很久以前提出的分层建图思想,得到了极大应用。
\(x,y\)坐标减小时付钱、加油时付钱、设加油站时付钱,这些我们都可以解决。关键是,\(K\)条边的限制怎么办?
这个时候,我们就可以按照剩余流量,分层建图。
令第\(0\)层为满油层,第\(K\)层为空油层。规定坐标\([z,x,y]\)的意义为:第\(z\)层的\((x,y)\)位置。
首先,对于一个加油站:
如果有\(z \neq 0\),连一条边\(([z,x,y],[0,x,y],INF,A)\)。
否则,即\(z=0\),向下一层的邻居节点连边。
这时候就有人问了,到加油站不是强制加油吗,为什么第\(0\)层时却不用加油?
因为第\(0\)层的状态只有在刚加满油的时候才会出现。其它时候,当你从其他地方开进一个加油站时,一定不会在第\(0\)层。
然后,对于一个非加油站:
默认可以建油站,连一条边\(([z,x,y],[0,x,y],INF,A+C)\)。
那又有问题了,同一个节点,油站建一次就行了凭什么再来时还要再建?
因为我们的路径必然无环。有环的局面必然是向上或向右绕路去加油的,但已经修了加油站,就不会再想着去绕路了。
同时,如果\(z \neq K\),可以向下一层的邻居节点连边。
关于源点和汇点,初始状态必然只有\((S,[0,0,0],1,0)\)一种。
但是对于所有的\(z\in [0,K]\),都可以有\(([z,n-1,n-1],T,1,0)\)。
所以图就建完了。答案即为最小费用最大流。
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,K,a,b,c,g[110][110],head[150100],cnt,id[150100],fr[150100],dis[150100],S,T,cost;
struct node{
int to,next,val,cost;
}edge[5010000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[150100];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x3f3f3f3f3f3f3f3f)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
signed main(){
scanf("%lld%lld%lld%lld%lld",&n,&K,&a,&b,&c),S=(K+1)*n*n+1,T=(K+1)*n*n+2,memset(head,-1,sizeof(head));
for(int i=0;i<n;i++)for(int j=0;j<n;j++)scanf("%lld",&g[i][j]);
for(int k=0;k<=K;k++)for(int i=0;i<n;i++)for(int j=0;j<n;j++){
if(g[i][j]){
ae(k*n*n+i*n+j,i*n+j,0x3f3f3f3f,a);
if(!k){
if(i+1<n)ae(k*n*n+i*n+j,(k+1)*n*n+(i+1)*n+j,0x3f3f3f3f,0);
if(j+1<n)ae(k*n*n+i*n+j,(k+1)*n*n+i*n+(j+1),0x3f3f3f3f,0);
if(i-1>=0)ae(k*n*n+i*n+j,(k+1)*n*n+(i-1)*n+j,0x3f3f3f3f,b);
if(j-1>=0)ae(k*n*n+i*n+j,(k+1)*n*n+i*n+(j-1),0x3f3f3f3f,b);
}
}
else{
ae(k*n*n+i*n+j,i*n+j,0x3f3f3f3f,a+c);
if(k!=K){
if(i+1<n)ae(k*n*n+i*n+j,(k+1)*n*n+(i+1)*n+j,0x3f3f3f3f,0);
if(j+1<n)ae(k*n*n+i*n+j,(k+1)*n*n+i*n+(j+1),0x3f3f3f3f,0);
if(i-1>=0)ae(k*n*n+i*n+j,(k+1)*n*n+(i-1)*n+j,0x3f3f3f3f,b);
if(j-1>=0)ae(k*n*n+i*n+j,(k+1)*n*n+i*n+(j-1),0x3f3f3f3f,b);
}
}
}
ae(S,0,1,0);
for(int k=0;k<=K;k++)ae(k*n*n+n*n-1,T,1,0);
while(SPFA());
printf("%lld\n",cost);
return 0;
}
XXVIII.[SCOI2007]修车
一道很好的题。
一开始方向就想歪了,想着排序之后瞎建图,结果一直爆0。
看了题解
我们将每个工人拆成\(n\)个点,表示工人修的倒数第\(1\)到第\(n\)辆车。如果一辆车\(k\)是\(i\)工人修的倒数第\(j\)辆车,它将贡献\(time_{i,k}\times j\)单位的时间(为它自己和它后面的\(j\)辆车各增加了\(time_{i,k}\)的时间)。
建完图后跑最小费用最大流。答案即为\(cost\)。
代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,head[10100],dis[10100],id[10100],fr[10100],cnt,cost,S,T;
struct node{
int to,next,val,cost;
}edge[501000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[10100];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==0x3f3f3f3f)return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
signed main(){
scanf("%d%d",&m,&n),memset(head,-1,sizeof(head)),S=m*n+n+1,T=m*n+n+2;
for(int i=1;i<=n;i++)for(int j=1,x;j<=m;j++){
scanf("%d",&x),ae((i-1)*m+j,T,1,0);
for(int k=1;k<=n;k++)ae(n*m+i,(k-1)*m+j,1,k*x);
}
for(int i=1;i<=n;i++)ae(S,n*m+i,1,0);
while(SPFA());
printf("%.2lf\n",(double)cost/n);
return 0;
}
XXXI.【模板】最小割树(Gomory-Hu Tree)
这就是那道最小割树的模板竟然是黑题上一道题才紫题。
相信如果上一道题看懂了这题也没问题了。
主要是上一题没有真正地把树建出来,但这题必须得建树。
为了减少码量,我没有写倍增\(LCA\),而是采取暴力跳\(LCA\)的办法反正\(n\)才\(500\)。
代码:
#include<bits/stdc++.h>
using namespace std;
int head[1010],h[1010],c,cnt,dep[1010],cur[1010],n,m,S,T,res,ord[1010],fa[1010],val[1010];
struct TREE{
int to,next,val;
}e[400100];
void AE(int u,int v,int w){
// printf("%d %d %d\n",u,v,w);
e[c].next=h[u],e[c].to=v,e[c].val=w,h[u]=c++;
}
struct node{
int to,next,val,ini;
}edge[400100];
void ae(int u,int v,int w){
// printf("%d %d %d\n",u,v,w);
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=edge[cnt].ini=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=edge[cnt].ini=w,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep));
q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
inline void initialize(){
for(int i=0;i<cnt;i++)edge[i].val=edge[i].ini;
}
bool cmp(int x,int y){
return dep[x]<dep[y];
}
void work(int l,int r){
if(l==r)return;
S=ord[l],T=ord[r],res=0;
Dinic(),AE(ord[l],ord[r],res),AE(ord[r],ord[l],res),initialize();
sort(ord+l,ord+r+1,cmp);
int cut=0;
for(int i=l;i<=r;i++)if(dep[ord[i]]){cut=i;break;}
work(l,cut-1),work(cut,r);
}
void DEP(int x){
for(int i=h[x];i!=-1;i=e[i].next)if(e[i].to!=fa[x])fa[e[i].to]=x,val[e[i].to]=e[i].val,dep[e[i].to]=dep[x]+1,DEP(e[i].to);
}
int query(int x,int y){
int ans=0x3f3f3f3f;
if(dep[x]>dep[y])swap(x,y);
while(dep[x]<dep[y])ans=min(ans,val[y]),y=fa[y];
while(x!=y)ans=min(ans,min(val[x],val[y])),x=fa[x],y=fa[y];
return ans;
}
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),memset(h,-1,sizeof(head));
for(int i=1,x,y,z;i<=m;i++)scanf("%d%d%d",&x,&y,&z),ae(x,y,z);
for(int i=0;i<=n;i++)ord[i]=i;
// puts("");
work(0,n);
dep[0]=0,fa[0]=-1,val[0]=0x3f3f3f3f;
DEP(0);
scanf("%d",&m);
for(int i=1,x,y;i<=m;i++)scanf("%d%d",&x,&y),printf("%d\n",query(x,y));
return 0;
}
XXXII.[ZJOI2011]最小割
又是近似的模板题QaQ……
我们没有什么好办法去求出容量不超过\(x\)的点对数量,但\(n\)只有\(150\),所以我们可以先\(n^3\)暴力求出所有点对的距离,压入\(vector\)中排序,之后二分即可。
坑点:在两组测试数据之间需要输出一行空行。
代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
int TT,head[180],h[180],c,cnt,dep[180],cur[180],n,m,S,T,res,ord[180],fa[180],val[180];
struct TREE{
int to,next,val;
}e[400100];
void AE(int u,int v,int w){
// printf("%d %d %d\n",u,v,w);
e[c].next=h[u],e[c].to=v,e[c].val=w,h[u]=c++;
}
struct node{
int to,next,val,ini;
}edge[400100];
void ae(int u,int v,int w){
// printf("%d %d %d\n",u,v,w);
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=edge[cnt].ini=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=edge[cnt].ini=w,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep));
q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f3f3f3f3f);
}
}
inline void initialize(){
for(int i=0;i<cnt;i++)edge[i].val=edge[i].ini;
}
bool cmp(int x,int y){
return dep[x]<dep[y];
}
void work(int l,int r){
if(l==r)return;
S=ord[l],T=ord[r],res=0;
Dinic(),AE(ord[l],ord[r],res),AE(ord[r],ord[l],res),initialize();
sort(ord+l,ord+r+1,cmp);
int cut=0;
for(int i=l;i<=r;i++)if(dep[ord[i]]){cut=i;break;}
work(l,cut-1),work(cut,r);
}
void DEP(int x){
for(int i=h[x];i!=-1;i=e[i].next)if(e[i].to!=fa[x])fa[e[i].to]=x,val[e[i].to]=e[i].val,dep[e[i].to]=dep[x]+1,DEP(e[i].to);
}
int query(int x,int y){
int ans=0x3f3f3f3f3f3f3f3f;
if(dep[x]>dep[y])swap(x,y);
while(dep[x]<dep[y])ans=min(ans,val[y]),y=fa[y];
while(x!=y)ans=min(ans,min(val[x],val[y])),x=fa[x],y=fa[y];
return ans;
}
vector<int>v;
signed main(){
scanf("%lld",&TT);
while(TT--){
scanf("%lld%lld",&n,&m),memset(head,-1,sizeof(head)),memset(h,-1,sizeof(head)),cnt=c=0,v.clear();
for(int i=1,x,y,z;i<=m;i++)scanf("%lld%lld%lld",&x,&y,&z),ae(x,y,z);
for(int i=1;i<=n;i++)ord[i]=i;
work(1,n);
dep[1]=0,fa[1]=-1,val[1]=0x3f3f3f3f3f3f3f3f;
DEP(1);
for(int i=1;i<=n;i++)for(int j=i+1;j<=n;j++)v.push_back(query(i,j));
sort(v.begin(),v.end());
scanf("%lld",&m);
for(int i=1,x;i<=m;i++)scanf("%lld",&x),printf("%lld\n",upper_bound(v.begin(),v.end(),x)-v.begin());
puts("");
}
return 0;
}
XXXIII.[NOI2008]志愿者招募
这题与最长k可重线段集问题是类似的题目,也是单个物品可以限制住多个位置。于是我们就可以按照老套路链式建图。
对于\(\forall i \in [1,n]\),连边\((i,i+1,INF-a_i,0)\)。同时连边\((S,1,INF,0)\)与\((n+1,T,INF,0)\)。这样,为了补全损失的\(a_i\)单位流量,最大流不得不尝试从我们接下来要连的边中选择一些边。
对于\(\forall i \in [1,m]\),连边\((s_i,t_i+1,INF,c_i)\)。表示有一条边可以在\([s_i,t_i]\)的范围内弥补流量。
这样,对于源点出发的\(INF\)单位流量,它们大部分会走入我们一开始连的边。然而,有小部分被卡住了,只能走我们后来连的新边。这样我们就实现了这一算法。
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int S,T,n,m,head[1010],cnt,dis[1010],fr[1010],id[1010],cost;
struct node{
int to,next,val,cost;
}edge[101000];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[1010];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[0])return false;
int x=T,mn=0x3f3f3f3f3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=mn*dis[T],x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
signed main(){
scanf("%lld%lld",&n,&m),memset(head,-1,sizeof(head)),S=n+2,T=n+3,ae(S,1,0x3f3f3f3f3f3f3f3f,0),ae(n+1,T,0x3f3f3f3f3f3f3f3f,0);
for(int i=1,x;i<=n;i++)scanf("%lld",&x),ae(i,i+1,0x3f3f3f3f3f3f3f3f-x,0);
for(int i=1,x,y,z;i<=m;i++)scanf("%lld%lld%lld",&x,&y,&z),ae(x,y+1,0x3f3f3f3f3f3f3f3f,z);
while(SPFA());
printf("%lld\n",cost);
return 0;
}
XLI.OPTM - Optimal Marks
神题orz……
这题属于一看就不会做的类型。
首先,观察到异或运算对于各二进制位是相互独立的。因此,我们可以按位处理。
对于单独的某一位,所有的点权要么为\(1\),要么为\(0\),要么没填。我们可以将所有的点归为两个集合,\(0\)集合和\(1\)集合。显然,只有连接两个集合之间的边才有贡献,但集合内部的边没有贡献。
联想到最小割模型也是将所有点归为两个集合,\(\mathbb{S}\)集合和\(\mathbb{T}\)集合,并且只有连接两个集合的边才有贡献。我们可以借鉴思想。
对于所有的\(1\)点,连边\((S,i,INF)\),表示这个点默认必在\(\mathbb{S}\)集合,即\(1\)集合中;对于所有的\(0\)点,连边\((i,T,INF)\),表示这个点默认必在\(\mathbb{T}\)集合,即\(0\)集合中。
对于所有原图中的边,连双向边\((x,y,1)\)。如果这条边被割断,则\(x\)和\(y\)就分属两个不同的集合。
最终,所有属于\(\mathbb{S}\)集合的点,这一位都是\(1\);所有属于\(\mathbb{T}\)集合的点,这一位都是\(0\)。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int TT,n,m,k,val[510],ans[510];
namespace MaxFlow{
const int N=510,M=30100;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
pair<int,int>p[3010];
int main(){
scanf("%d",&TT);
while(TT--){
scanf("%d%d",&n,&m),memset(val,-1,sizeof(val)),memset(ans,0,sizeof(ans)),S=n+1,T=n+2;
for(int i=1;i<=m;i++)scanf("%d%d",&p[i].first,&p[i].second);
scanf("%d",&k);
for(int i=1,x,y;i<=k;i++)scanf("%d%d",&x,&y),val[x]=y;
for(int i=0;i<32;i++){
memset(head,-1,sizeof(head)),cnt=res=0;
for(int j=1;j<=n;j++){
if(val[j]==-1)continue;
if(val[j]&(1<<i))ae(S,j,0x3f3f3f3f),ae(j,S,0);
else ae(j,T,0x3f3f3f3f),ae(T,j,0);
}
for(int j=1;j<=m;j++)ae(p[j].first,p[j].second,1),ae(p[j].second,p[j].first,1);
Dinic();
for(int j=1;j<=n;j++)if(dep[j])ans[j]+=(1<<i);
}
for(int i=1;i<=n;i++)printf("%d\n",ans[i]);
}
return 0;
}
XLIII.[SDOI2010]星际竞速
这题稍微一看就像是最小路径覆盖问题的升级版:
都是有向无环图(点之间有时间关系,不可能出现环)
都可以看作是多条路径的并(一次跃迁就相当于开始一条新的路径)
每个点都能且只能经过一次。
因此我们可以考虑和那题一样的做法:拆点。
方法还是一样,拆成\(in\)和\(out\)两个点。对于\(\forall i \in \mathbb{V}\),连边\((S,in_i,1,0),(out_i,T,1,0)\)。对于所有的\((x,y,z)\in \mathbb{E}\),连边\((in_x,out_y,1,z)\)。
这些操作都好理解。如果某条边\((in_x,out_y,1,z)\)出现在了最大流中,则说明最终的方案中经过了\(x\rightarrow y\)。
如果某个\(in_x\)没有任何出现在最大流中的出边,则说明它是某段路径的终点,接下来他进行了一次跃迁。
那么跃迁的花费怎么算呢?
对于\(\forall i \in \mathbb{V}\),连边\((S,out_i,1,A_i)\),其中\(A_i\)表示定位时间。
为什么呢?
首先,这么一连,就能够保证最大流一定为\(n\)。
同时,当这条路径被启用,就意味着这个星球是某次跃迁的终点,即某段路径的起点。
则每一条最大流,都对应着原图中的一条方案。最小费用最大流,就意为着所有方案中最优的那一条。
则答案即为最小费用。
代码:
#include<bits/stdc++.h>
using namespace std;
int n,m;
namespace MCMF{
const int N=2010,M=200000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[0])return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
using namespace MCMF;
int main(){
scanf("%d%d",&n,&m),S=2*n+1,T=2*n+2,memset(head,-1,sizeof(head));
for(int i=1,x;i<=n;i++)scanf("%d",&x),ae(S,i+n,1,x),ae(S,i,1,0),ae(i+n,T,1,0);
for(int i=1,x,y,z;i<=m;i++){
scanf("%d%d%d",&x,&y,&z);
if(x>y)swap(x,y);
ae(x,y+n,1,z);
}
while(SPFA());
printf("%d\n",cost);
return 0;
}
XLIV.[六省联考2017]寿司餐厅
又是一道魔鬼题QaQ……
根本不会做,就连题解也只能勉强看懂……
首先,我们需要回忆一下多年前在VI.[NOI2009]植物大战僵尸中提出的最大权闭合子图的概念。
对于这道题,我们完全可以抽象出这个模型出来:
1.如果你选择了一个大区间,则小区间也必然被选,即:
当\(i<j\)时,如果选择\(d_{i,j}\),必选择\(d_{i+1,j}\)与\(d_{i,j+1}\)。
2.如果你选择了某单个寿司,则相当于你这种代号必须得选。
具体地说,为了处理这个\(mx^2,m\in[0,1]\),我们建立代号节点\(id_x\)。对于每个\(d_{i,i}\),必选\(id_{a_i}\)。
而每个点都有相应的费用:
对于区间节点,有\(d_{i,j}\)的利益;
对于单个寿司(即\(d_{i,i}\)),有\(a_i\)的费用;
对于代号节点,若\(m=1\),有\(id_x^2\)的费用。
因此我们就可以建图了。
首先,老套路,对于\(\forall i \in [1,n],j \in [i,n]\),若\(d_{i,j}\geq 0\),连边\((S,(i,j),d_{i,j})\);若\(d_{i,j} \leq 0\),连边\(((i,j),T,d_{i,j})\)。
特别地,对于\(\forall i \in [1,n]\),这个\(d_{i,i}\)应该减去\(a_i\),因为取它还要耗费\(a_i\)的费用,不如直接同利益一起计算。
对于\(\forall i \in [1,n],j \in (i,n]\),连边\(((i,j),(i+1,j),INF)\)与\(((i,j),(i,j-1),INF)\)。
另外,若\(m=1\):
\(\forall i \in [1,n]\),连边\(((i,i),id_{a_i},INF)\);
对于$\forall i \(,连边\)(id_i,T,id_i^2)$。
然后我们就完成了这个问题。
答案为\((\sum\limits_{d_{i,j}\geq 0} d_{i,j})-cut\),其中\(cut\)为最小割。
代码:
#include<bits/stdc++.h>
using namespace std;
const int K=1000;
int n,m,sum,tp[1010];
namespace MaxFlow{
const int N=100000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=99998,T=99999;
for(int i=0,x;i<n;i++)scanf("%d",&tp[i]);
if(m)for(int i=1;i<=K;i++)ae(n*n+i,T,i*i);
for(int i=0;i<n;i++)for(int j=i,x;j<n;j++){
scanf("%d",&x);
if(i==j){
x-=tp[i];
if(m)ae(i*n+j,n*n+tp[i],0x3f3f3f3f);
}
if(x>0)ae(S,i*n+j,x),sum+=x;
if(x<0)ae(i*n+j,T,-x);
if(i!=j)ae(i*n+j,(i+1)*n+j,0x3f3f3f3f),ae(i*n+j,i*n+(j-1),0x3f3f3f3f);
}
Dinic();
printf("%d\n",sum-res);
return 0;
}
XLV.[TJOI2015]线性代数
这题必须得好好讲讲。
(接下来的表述可能有些不规范,例如用一个\(1*1\)矩阵来代表它的值,或者行列向量不分,或者下表不对劲等,不过理解就行)
我们有
\(D=(A*B-C)*A^T\),
设\(A*B-C=E\),
则\(E_{i,j}=(\Sigma A_{i,k}*B_{k,j})-C_{i,j}\)
因为\(E\)是\(1*n\)矩阵,故有:
\(E_i=(\Sigma A_j*B_{j,i})-C_i\)
我们有\(D=E*A^T\),
即\(D=\Sigma E_i*A^T_i\)
由于不太规范的表述,实际上\(A^T_i=A_i\)(但只是值相等),因此我们仍可以这么说:
\(D=\Sigma E_i*A_i\)
即\(D=\sum\limits_{i=1}^n(\sum\limits_{j=1}^nA_j*B_{j,i}-C_i)*A_i\)
化简得\(D=\sum\limits_{i=1}^n\sum\limits_{j=1}^nA_i*A_j*B_{i,j}-A_i*C_i\)
也就是说,我们每有一个\(A_i=1\),都要有\(C_i\)的费用;
但是,每有一对有序数对\((i,j)\)使得\(A_i=A_j=1\),都有\(B_{i,j}\)的贡献。
这很像最小割的模型。
我们画出图来:
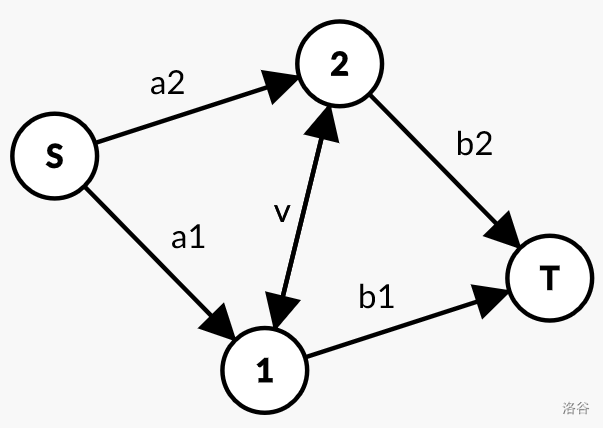
设\(\mathbb{S}\)集合为\(A_i=1\)的集合,\(\mathbb{T}\)集合为\(A_i=0\)的集合。
因为要让\(A_i=1\),必要割掉\((i,T)\),而割掉费用即为\(C_i\),则\(b1=C_i,b2=C_j\)
我们已经得到了如下的方程组:
\(\begin{cases}a1+a2=B_{i,j}+B_{j,i}\text{(如果割去到S的边,即两个都选0,就会损失所有与i,j有关的B)}\\a1+v+b2=B_{i,j}+B_{j,i}+C_i\text{(如果只有j选1,则只有Cj与Bjj可以保留)}\\a2+v+b1=B_{i,j}+B_{j,i}+C_j\text{(如果只有i选1,则只有Ci与Bii可以保留)}\end{cases}\)
(虽然我的做法是借鉴第一篇题解的,但我自认为他的做法好像有毛病,\(B_{i,i},B_{j,j}\)这两个东西不应计入。)
解得:
\(\begin{cases}v=\dfrac{B_{i,j}+B_{j,i}}{2}\\a1=\dfrac{B_{i,j}+B_{j,i}}{2}\\a2=\dfrac{B_{i,j}+B_{j,i}}{2}\end{cases}\)
令人惊异的是,\(v=a1=a2\),方程组说明了这一点。
则最终,边\((S,i)\)的边权即为\(B_{i,i}+\sum\limits_{j=1,j\neq i}^n\dfrac{B_{i,j}+B_{j,i}}{2}=\dfrac{\sum\limits_{j=1}^nB_{i,j}+B_{j,i}}{2}\)。
边\((i,j)\)的边权为\(\dfrac{B_{i,j}+B_{j,i}}{2}\)。
边\((i,T)\)的边权为\(C_i\)。
为了避免小数,所有的边权\(\times 2\),只要将最终的最大流\(\div 2\)即可。
这是理论给出的答案。众所周知,理论的东西不可盲从。那么实际呢?
看我的主函数:
int main(){
scanf("%d",&n),memset(head,-1,sizeof(head)),S=n+1,T=n+2;
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)scanf("%d",&b[i][j]),sum+=b[i][j];
for(int i=1;i<=n;i++)scanf("%d",&c[i]);
for(int i=1;i<=n;i++){
int s=0;
for(int j=1;j<=n;j++)s+=b[i][j]+b[j][i];
ae(S,i,s),ae(i,S,0),ae(i,T,c[i]),ae(T,i,0);
}
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)ae(i,j,b[i][j]+b[j][i]);
Dinic();
printf("%d\n",sum-res);
return 0;
}
可以发现,边权没有\(\times 2\),最大流也没有\(\div 2\),为什么呢?
我也不知道啊。
只能希望有什么巨佬能够解答我的疑惑。
不过,这份理论上错误的代码却取得了满分的成绩。
至于原因,我不知道。
XLVI.[HNOI2013]切糕
这题给我两个很深的忠告:一是拆点不能乱用,二是网络流题思路一定要完全清晰,如果思路尽管大体准确但有少量不清晰的地方就仍然无法写出正确的代码。
我们很容易就能想到最小割的模型。
首先,因为每行每列(或者说,每个竖条),只能选一个位置,因此我们可以把每个竖条串成一列,或者,对于\(\forall i,j,k\),连边\(((i,j,k),(i,j,k+1),v_{i,j,k})\)。注意这样做需要额外增加第\(r+1\)层。
然后,对于第\(1\)层的所有点,即\(\forall i,j\),连边\((S,(i,j,1),INF)\)。对于第\(r+1\)层的所有点,即\(\forall i,j\),连边\(((i,j,r+1),T,INF)\)。这样我们就完成了在不管\(D\)时的建模。
考虑上\(D\)后,我们应该怎么办呢?
首先,
\(|f(x,y)-f(i,j)|\leq D\Leftrightarrow 0\leq f(x,y)-f(i,j)\leq D \ or\ 0\leq f(i,j)-f(x,y)\leq D\)。
则我们只要考虑一端的状况,即\(0\leq f(x,y)-f(i,j)\leq D\)时即可。
这意味着,当相邻两格的层数差超过\(D\)时,就算两格都割断,也不是一组合法的割集。
我们对于\(\forall i \in [D+1,R+1],j,k\),都连边\(((j,k,i),(x,y,i-D),INF)\),其中格\((x,y)\)与格\((i,j)\)相邻。
为什么这样就可以了呢?
首先,这种连法适用于\(f(i,j)-f(x,y)>D\)的情形。
当你割去比\((i-D)\)还要低的点时,从\((j,k,i)\)而来的流量会直接通到\((i-D)\)去,并不能割断。只有你割断高于\((i-D)\)的点,才能是一组真正的割。
代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,r,d,mat[50][50][50],dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};
bool invalid(int y,int z){
return y>=n||y<0||z>=m||z<0;
}
namespace MaxFlow{
const int N=200000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d%d%d",&n,&m,&r,&d),memset(head,-1,sizeof(head)),S=(r+1)*n*m,T=(r+1)*n*m+1;
for(int i=0;i<r;i++)for(int j=0;j<n;j++)for(int k=0;k<m;k++)scanf("%d",&mat[i][j][k]);
for(int i=0;i<n;i++)for(int j=0;j<m;j++)ae(S,i*m+j,0x3f3f3f3f),ae(n*m*r+i*m+j,T,0x3f3f3f3f);
for(int i=0;i<r;i++)for(int j=0;j<n;j++)for(int k=0;k<m;k++){
ae(i*n*m+j*m+k,(i+1)*n*m+j*m+k,mat[i][j][k]);
for(int l=0;l<4;l++){
if(invalid(j+dx[l],k+dy[l]))continue;
int h=i-d;
if(h>=0)ae(i*n*m+j*m+k,h*n*m+(j+dx[l])*m+(k+dy[l]),0x3f3f3f3f);
}
}
Dinic();
printf("%d\n",res);
return 0;
}
XLVIII.文理分科
这里我们介绍一种新建图方法:对偶建图(名字我瞎起的)。
这种建图方法来源于网络流的特性:对偶性(又是我瞎起的),即:当你调换一张网络的源点和汇点,并将所有的边反向,得到的新网络的最大流同原图一致。
如果你得到的输入也具有对偶性,即:按照一定规则调换输入顺序对答案没有影响,例如这道题中将文理科的所有东西全部互换,答案不变,或许就可以尝试对偶建图。
最好的状况是,它具有非黑即白的性质,在这道题中,是一个人要么选理科,要么选文科。
首先,对于这道题,一眼看上去就是最小割。
如果没有相邻奖励的条件,你会怎么做?
贪心
正确的做法是,对于每个学生\((i,j)\),从源点连来\(art_{i,j}\)的流量,并向汇点连去\(science_{i,j}\)的流量。这样,显然,(总和-最小割)即为答案。
显然,这符合对偶性,因为你让\(science\)连去源点并让\(art\)连到汇点亦可。
考虑相邻奖励的条件。我们开两个节点\((i,j)_1\)与\((i,j)_2\),分别表示\(sameart\)的奖励节点与\(samescience\)的奖励节点。
我们连边\(((x,y),(i,j)_1,INF)\),当\((i,j)\)与\((x,y)\)相邻。我们同时连边\((S,(i,j)_1,sameart_{i,j})\)。这样的话,只有所有的\(((x,y),T)\)都被割断,即所有的\((x,y)\)都选文科,\((i,j)_1\)才与汇点不连通,\(sameart_{i,j}\)才能被选。否则,只要有一条\(((x,y),T)\)没被割断,\((S,(i,j)_1)\)就必须为了满足割集的条件而被割断。
对于理科亦然。
做对偶建图的题和写对偶建图的博客都需要把同一段代码复制两遍,因为对偶性
代码:
#include<bits/stdc++.h>
using namespace std;
#define O(i,j) (i*m+j)
#define C(i,j) (i*m+j+n*m)
#define D(i,j) (i*m+j+n*m*2)
int n,m,a[110][110],b[110][110],c[110][110],d[110][100],dx[5]={0,1,0,-1,0},dy[5]={0,0,1,0,-1},sum;
namespace MaxFlow{
const int N=300000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=n*m*3+1,T=n*m*3+2;
for(int i=0;i<n;i++)for(int j=0;j<m;j++)scanf("%d",&a[i][j]),ae(S,O(i,j),a[i][j]),sum+=a[i][j];
for(int i=0;i<n;i++)for(int j=0;j<m;j++)scanf("%d",&b[i][j]),ae(O(i,j),T,b[i][j]),sum+=b[i][j];
for(int i=0;i<n;i++)for(int j=0;j<m;j++){
scanf("%d",&c[i][j]),ae(S,C(i,j),c[i][j]),sum+=c[i][j];
for(int k=0;k<5;k++){
int x=i+dx[k],y=j+dy[k];
if(x>=n||x<0||y>=m||y<0)continue;
ae(C(i,j),O(x,y),0x3f3f3f3f);
}
}
for(int i=0;i<n;i++)for(int j=0;j<m;j++){
scanf("%d",&d[i][j]),ae(D(i,j),T,d[i][j]),sum+=d[i][j];
for(int k=0;k<5;k++){
int x=i+dx[k],y=j+dy[k];
if(x>=n||x<0||y>=m||y<0)continue;
ae(O(x,y),D(i,j),0x3f3f3f3f);
}
}
Dinic();
printf("%d\n",sum-res);
return 0;
}
LVII.[CQOI2014]危桥
这题比较妙。
首先,很容易就能想到,一次往返可以变成单次过去,只要将危桥的通过次数设成\(1\)即可(一来一往桥就塌了,故只能过一次)。
但是,这是双向边。很担心可能会出现\(A\)从桥上过去,\(B\)从桥对岸过来的剧情。
然后就不会了。
结果,只要在第一遍时,源点连到\(a1\)和\(b1\),\(a2\)和\(b2\)连到汇点,跑最大流;第二遍,源点连到\(a1\)和\(b2\),\(a2\)和\(b1\)连到汇点,再跑一遍最大流。如果两次都满流,则合法。
为什么呢?
首先,之前我们说的那种情况就不可能发生了。第一次\(B\)与\(A\)的方向是反的,第二次可就正过来了。其次,还有可能就是\(A\)的一部分流量流到\(B\),\(B\)的一部分流量流到\(A\)的情形。但是可以证明反正我不会证,不可能两次这种情况都发生。
然后就A了。
代码:
#include<bits/stdc++.h>
using namespace std;
int n,a1,a2,an,b1,b2,bn;
char s[100][100];
namespace MaxFlow{
const int N=1000,M=200000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
void AE(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
int main(){
while(scanf("%d%d%d%d%d%d%d",&n,&a1,&a2,&an,&b1,&b2,&bn)!=EOF){
S=n,T=n+1;
for(int i=0;i<n;i++)scanf("%s",s[i]);
memset(head,-1,sizeof(head)),cnt=res=0;
for(int i=0;i<n;i++)for(int j=0;j<n;j++)if(s[i][j]=='O')ae(i,j,1);else if(s[i][j]=='N')ae(i,j,0x3f3f3f3f);
ae(S,a1,an),ae(a2,T,an),ae(S,b1,bn),ae(b2,T,bn);
Dinic();
if(res!=an+bn){puts("No");continue;}
memset(head,-1,sizeof(head)),cnt=res=0;
for(int i=0;i<n;i++)for(int j=0;j<n;j++)if(s[i][j]=='O')ae(i,j,1);else if(s[i][j]=='N')ae(i,j,0x3f3f3f3f);
ae(S,a1,an),ae(a2,T,an),ae(S,b2,bn),ae(b1,T,bn);
Dinic();
if(res!=an+bn){puts("No");continue;}
puts("Yes");
}
return 0;
}
LX.[SCOI2012]奇怪的游戏
一眼看出奇偶建图。同时也想到了\(n\times m\)为奇和为偶的区别。但是剩下的也想不到了。因此看了题解。
这题果然神仙。
我们设奇点有\(W\)个,初始和为\(w\);偶点有\(B\)个,初始和为\(b\);最终状态下,每个点都是\(X\)。
则必有\(X\times W-w=X\times B-b\)(因为奇点和每增加\(1\),偶点和也必增加\(1\));
移项得\(X\times(W-B)=w-b\);
则有\(X=\dfrac{w-b}{W-B}\)。
等等,我们这么轻松就把最终的值解出来了?
并不是,我们忽略了\((W=B)\)的情况。此时,光凭这个方程是得不出\(X\)的值的。
\(W=B\)当且仅当\(n\times m\)为偶数。但是,当\(n\times m\)为偶数时,答案具有单调性。也就是说,如果\(X\)作为最终状态合法,所有\(>X\)的\(Y\)作为最终状态仍然合法。因为我们可以用\(\dfrac{n\times m}{2}\)次操作恰好使棋盘上每一个数增加\(1\)。
然后我们就可以二分了。每次,我们需要\(check\)一个\(mid\)作为最终状态是否合法。
等等,这不就是当\(n\times m\)为奇时,当我们解出\(X\)后,所要做的事吗?我们需要\(check\)能否构造出一个方案来满足这个\(X\)。
对于每一个点\(x\),设它的值为\(v_x\)。如果它是奇点,那么连边\((S,x,X-v_x)\),并对于它四联通的点\(y\)连边\((x,y,INF)\);如果它是偶点,连边\((x,T,X-v_x)\)。如果\(flow=\sum\limits_{\text{x是奇点}}X-v_x\),则这个\(X\)合法。
代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int T_T,n,m,mat[50][50],dx[4]={1,0,-1,0},dy[4]={0,1,0,-1},B,W,b,w,L,R,sum;
namespace MaxFlow{
const int N=2000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,9e18);
}
}
}
using namespace MaxFlow;
bool che(int ip){
memset(head,-1,sizeof(head)),cnt=res=sum=0;
for(int i=0;i<n;i++)for(int j=0;j<m;j++){
if((i+j)&1){
ae(S,i*m+j,ip-mat[i][j]),sum+=ip-mat[i][j];
for(int k=0;k<4;k++)if(i+dx[k]>=0&&i+dx[k]<n&&j+dy[k]>=0&&j+dy[k]<m)ae(i*m+j,(i+dx[k])*m+(j+dy[k]),1e16);
}else ae(i*m+j,T,ip-mat[i][j]);
}
Dinic();
// printf("%lld %lld\n",sum,res);
return sum==res;
}
signed main(){
scanf("%lld",&T_T);
while(T_T--){
scanf("%lld%lld",&n,&m),B=W=b=w=0,L=0,R=1e16,S=n*m,T=n*m+1;
for(int i=0;i<n;i++)for(int j=0;j<m;j++){
scanf("%lld",&mat[i][j]),L=max(L,mat[i][j]);
if((i+j)&1)B++,b+=mat[i][j];
else W++,w+=mat[i][j];
}
if(W!=B){
int X=(w-b)/(W-B);
if(X>=L&&che(X))printf("%lld\n",sum);
else puts("-1");
continue;
}
while(L<R){
int mid=(L+R)>>1;
// printf("%lld %lld %lld\n",L,R,mid);
if(che(mid))R=mid;
else L=mid+1;
}
if(!che(R))puts("-1");
else printf("%lld\n",sum);
}
return 0;
}
LXX.[AHOI2014/JSOI2014]支线剧情
这题就是典型的有上下界的费用流。
首先,每条边具有流量限制\([1,INF)\)(至少经过一次,但是经过次数无上限),以及费用\(t\)。
因此,我们就可以跑最小费用可行流了。方法和前一题完全一致,只是将最大流换成最小费用最大流。
另外,这题需要建立汇点\(t\),所有非\(1\)号节点的剧情点都要连到伪汇点,表示从这里结束了一次游戏。这条新边具有\(0\)的下界,\(INF\)的上界。
同时,为了将有源汇变成无源汇,我们连边\((t,s)\),具有\(0\)的下界,\(INF\)的上界。
代码:
#include<bits/stdc++.h>
using namespace std;
int n,s,t,degree[1000];
namespace MCMF{
const int N=1000,M=2000000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[0])return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
using namespace MCMF;
int main(){
scanf("%d",&n),memset(head,-1,sizeof(head)),s=1,t=n+1,S=n+2,T=n+3;
for(int i=1,t1,t2,t3;i<=n;i++){
scanf("%d",&t1);
if(i!=1)ae(i,t,0x3f3f3f3f,0);
while(t1--)scanf("%d%d",&t2,&t3),ae(i,t2,0x3f3f3f3f,t3),degree[i]--,degree[t2]++,cost+=t3;
}
for(int i=1;i<=n;i++)if(degree[i]>0)ae(S,i,degree[i],0);else ae(i,T,-degree[i],0);
ae(t,s,0x3f3f3f3f,0);
while(SPFA());
printf("%d\n",cost);
return 0;
}
LXXVII.CF1187G Gang Up
有了前面那么多题的铺垫,这题应该比较简单了。
就连我这种蒟蒻也能自己想出来这个建图(虽然某个上限算错而导致出了点小问题)。
我们回忆一下以前学过的某些知识点:
按时间建图:X.餐巾计划问题
差分建图:LXXIV.[WC2007]剪刀石头布
然后就可以了。
我们按照时间建图。设\(id_{i,j}\)表示\(i\)时刻的\(j\)节点,那么:
1.\(\forall (x,y)\in E\),连边\((id_{i,x},id_{i+1,y})\)。至于这个\(c\times a^2\),我们差分得到\(\sum\limits_{j=1}^a c(2j-1)=c\times a^2\)。也就是说,我们连(人数)条边\((id_{i,x},id_{i+1,y},1,c(2j-1))\)。
2.\(\forall x \in V\),连边\((id_{i,x},id_{i+1,x},INF,0)\),表示赖在这里就不走了
3.\(\forall x \in V\),连边\((S,id_{0,x},occ_x,0)\),其中\(occ_x\)表示\(x\)节点有多少个人。
4.连边\((id_{i,1},T,INF,c\times i)\)。
应该比较清晰,如果这么多题你都一道一道刷过来的话。
另:时刻最多到(点数+人数),这样就一定能够错开每一条边使所有的\(a\)都\(\leq 1\)。
代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,r,c,d,occ[100];
pair<int,int>p[100];
namespace MCMF{
const int N=10000,M=20000000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[N-1])return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
using namespace MCMF;
int main(){
scanf("%d%d%d%d%d",&n,&m,&r,&c,&d),memset(head,-1,sizeof(head)),S=(r+n+1)*n+1,T=(r+n+1)*n+2;
for(int i=1,x;i<=r;i++)scanf("%d",&x),occ[x]++;
for(int i=1;i<=m;i++)scanf("%d%d",&p[i].first,&p[i].second);
for(int i=0;i<r+n;i++)for(int j=1;j<=m;j++)for(int k=1;k<=r;k++)ae(i*n+p[j].first,(i+1)*n+p[j].second,1,(2*k-1)*d),ae(i*n+p[j].second,(i+1)*n+p[j].first,1,(2*k-1)*d);
for(int i=1;i<=r+n;i++){
ae(i*n+1,T,0x3f3f3f3f,i*c);
for(int j=2;j<=n;j++)ae((i-1)*n+j,i*n+j,0x3f3f3f3f,0);
}
for(int i=1;i<=n;i++)ae(S,i,occ[i],0);
while(SPFA());
printf("%d\n",cost);
return 0;
}
LXXVIII.[JSOI2009]球队收益 / 球队预算
这里介绍一种可以同差分建图配合食用的技巧:费用提前计算(没错,名字又是我瞎起的)。
这道题一眼就可以看出是差分建图,但是两个属性,球队胜了要花钱,负了还是要花钱,比较难以处理。
这时,我们先假设所有队在所有还未进行的比赛上全部输了。这样的话,一场比赛胜负出来时,负者没有影响,但是胜者有影响(胜场加一,负场减一)。
我们来看一下它具体有什么费用。设这场比赛前胜者胜\(a\)场,负\(b\)场,
则新增费用为
\(c(a+1)^2+d(b-1)^2-ca^2-db^2=c+d+2ac-2bd\)
显然,随着\(a\)的增加,\(b\)的减小,这个式子单调递增。
然后就是经典的差分建图了。
代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,tms[5010],a[5010],b[5010],c[5010],d[5010];
namespace MCMF{
const int N=10000,M=2000000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[0])return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
using namespace MCMF;
int main(){
scanf("%d%d",&n,&m),memset(head,-1,sizeof(head)),S=n+m+1,T=n+m+2;
for(int i=1;i<=n;i++)scanf("%d%d%d%d",&a[i],&b[i],&c[i],&d[i]);
for(int i=1,x,y;i<=m;i++)scanf("%d%d",&x,&y),tms[x]++,tms[y]++,ae(S,n+i,1,0),ae(n+i,x,1,0),ae(n+i,y,1,0);
for(int i=1;i<=n;i++){
cost+=c[i]*a[i]*a[i]+d[i]*(b[i]+tms[i])*(b[i]+tms[i]);
for(int j=0;j<tms[i];j++)ae(i,T,1,c[i]+d[i]+2*c[i]*(a[i]+j)-2*d[i]*(b[i]+tms[i]-j));
}
while(SPFA());
printf("%d\n",cost);
return 0;
}
LXXXVII.CF976F Minimal k-covering
很容易想到,这个奇怪的限制可以直接跑有上下界的网络流完事。但这个\(n,m\leq 2000\)如果对每一个\(k\)都跑一遍真的大丈夫?
我们想到,在残量网络中,增加新边后原图中的剩余流量是可以不加修改继续使用的。那么,我们是否能够随着\(k\)的变化来在图中增加流量呢?
抱歉,还真不行。因为这个\(k\)是网络流的下界,下界一变,那入度跟出度也会有变化,就会导致某些边边权的减少。而减少边权是不适用于残量网络的。
正难则反。当然,这不是叫你倒着枚举\(k\),而是考虑放弃上下界,将本题规约成常规网络流。
如果我们将源汇点和二分图左右部之间连边的边权赋为\(deg_i-k\)的话,则我们现在跑出的实际上是所有不应该选的边(想一想,\(deg_i-(deg_i-k)=deg_i\),并且因为这是上界,所以有\(flow\leq deg_i-k\),即\(deg_i-flow\geq k\),刚好是我们的限制)。
并且,如果我们这时候倒着枚举\(k\),则\(deg_i-k\)是递增的!!!
然后就行了。尽管一共要跑\(k\)次网络流,但是均摊\(O(\text{网络流期望复杂度(太玄学了)})\)。
代码:
#include<bits/stdc++.h>
using namespace std;
int n1,n2,m,deg[5010],id[5010],mn=0x3f3f3f3f;
namespace MaxFlow{
const int N=5000,M=2000000;
int head[N],cur[N],dep[N],cnt,S,T,res;
struct node{
int to,next,val;
}edge[M];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
queue<int>q;
inline bool bfs(){
memset(dep,0,sizeof(dep)),q.push(S),dep[S]=1;
while(!q.empty()){
register int x=q.front();q.pop();
for(register int i=cur[x]=head[x];i!=-1;i=edge[i].next)if(edge[i].val&&!dep[edge[i].to])dep[edge[i].to]=dep[x]+1,q.push(edge[i].to);
}
return dep[T]>0;
}
bool reach;
inline int dfs(int x,int flow){
if(x==T){
res+=flow;
reach=true;
return flow;
}
int used=0;
for(register int &i=cur[x];i!=-1;i=edge[i].next){
if(!edge[i].val||dep[edge[i].to]!=dep[x]+1)continue;
register int ff=dfs(edge[i].to,min(edge[i].val,flow-used));
if(ff){
edge[i].val-=ff;
edge[i^1].val+=ff;
used+=ff;
if(used==flow)break;
}
}
return used;
}
inline void Dinic(){
while(bfs()){
reach=true;
while(reach)reach=false,dfs(S,0x3f3f3f3f);
}
}
}
using namespace MaxFlow;
vector<int>v[5010];
int main(){
scanf("%d%d%d",&n1,&n2,&m),memset(head,-1,sizeof(head)),S=n1+n2+1,T=n1+n2+2;
for(int i=1,x,y;i<=m;i++)scanf("%d%d",&x,&y),ae(x,y+n1,1),deg[x]++,deg[y+n1]++;
for(int i=1;i<=n1+n2;i++)mn=min(mn,deg[i]);
for(int i=1;i<=n1;i++)id[i]=cnt,ae(S,i,deg[i]-mn);
for(int i=n1+1;i<=n1+n2;i++)id[i]=cnt,ae(i,T,deg[i]-mn);
for(int i=0;i<=mn;i++){
Dinic();
for(int j=0;j<m;j++)if(edge[j<<1].val)v[i].push_back(j+1);
for(int j=1;j<=n1+n2;j++)edge[id[j]].val++;
}
for(int i=mn;i>=0;i--){
printf("%d ",v[i].size());
for(int j=0;j<v[i].size();j++)printf("%d ",v[i][j]);puts("");
}
return 0;
}
XCV.CF1288F Red-Blue Graph
最小费用可行流,题解。
XCVIII.UOJ#575. 【ULR #1】光伏元件
多年没碰过网络流了,这次碰到居然能做出来,真神奇。
一看到这奇奇怪怪的限制,就可以往网络流方面想了。因为它对每行每列上的流量上下界有限制,故我们很轻松就能想到将每一行每一列单独建一个点表示,将每个格子上的元件看作从行点连向列点的边,然后限制从源点连来行点的流量以及从列点连来汇点的流量。
但是,这无法保证“行与列差不大于定值”。
经过一番奇奇怪怪的思考,就产生了一个好想法:如果我们对于第 \(i\) 行和第 \(i\) 列,单独为它们开一对源汇点,然后每一行每一列对应的源汇点再连到总的源汇点,显然仍然是成立的;然后,为了保证差不大于定值,我们合并全部源汇点对(包括行列上的点对和总的点对)。
合并后的源汇点,我们给它起个名字,叫继点(瞎起名字*1)。这样,一对行列就对应了一个继点(称作分继点)。分继点可能有盈余流量(此时列上收到流量大于行上流出流量),也可能有亏空(此时与之前情形相反),也可能不赚不赔。但是,我们只需保证此盈亏范围在 \(k\) 以内即可。于是,我们从分继点连到总继点(总的源汇点对合并的产物)一条流量上限为 \(k\) 的无向边。这样,如果有亏损,无向边会从总点连向分点;反之,则从分点连向总点。明显,总点的流量也肯定是平衡的。
我们已经把图建出来了,那剩下的就上一个无源汇最小费用可行流就完事了。
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=305;
int n;
bool a[110][110];
int c[110][110];
namespace REF{//restricted flow
namespace MCMF{
const int M=200000;
int head[N],cnt,dis[N],fr[N],id[N],S,T,cost;
struct node{
int to,next,val,cost;
}edge[M];
void ae(int u,int v,int w,int c){
edge[cnt].cost=c,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=-c,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=0,head[v]=cnt++;
}
void AE(int u,int v,int w){//add a double-directed edge.
edge[cnt].cost=0,edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].cost=0,edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
queue<int>q;
bool in[N];
bool SPFA(){
memset(dis,0x3f,sizeof(dis)),dis[S]=0,q.push(S),in[S]=true;
while(!q.empty()){
int x=q.front();q.pop(),in[x]=false;
// printf("%d\n",x);
for(int i=head[x];i!=-1;i=edge[i].next){
if(!edge[i].val)continue;
if(dis[edge[i].to]>dis[x]+edge[i].cost){
dis[edge[i].to]=dis[x]+edge[i].cost,fr[edge[i].to]=x,id[edge[i].to]=i;
if(!in[edge[i].to])in[edge[i].to]=true,q.push(edge[i].to);
}
}
}
if(dis[T]==dis[0])return false;
int x=T,mn=0x3f3f3f3f;
while(x!=S)mn=min(mn,edge[id[x]].val),x=fr[x];
cost+=dis[T]*mn,x=T;
while(x!=S)edge[id[x]].val-=mn,edge[id[x]^1].val+=mn,x=fr[x];
return true;
}
}
int deg[N],O;
void init(){
memset(MCMF::head,-1,sizeof(MCMF::head));
O=3*n+1;
MCMF::S=3*n+2,MCMF::T=3*n+3;
}
void ae(int u,int v,int l,int r,int c){//add an single-directed edge
MCMF::ae(u,v,r-l,c);
MCMF::cost+=l*c;
deg[v]+=l,deg[u]-=l;
}
void func(){
for(int i=1;i<=O;i++){
if(deg[i]>0)MCMF::ae(MCMF::S,i,deg[i],0);
if(deg[i]<0)MCMF::ae(i,MCMF::T,-deg[i],0);
}
while(MCMF::SPFA());
}
}
int id[110][110];
int main(){
scanf("%d",&n),REF::init();
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)scanf("%d",&a[i][j]);
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)scanf("%d",&c[i][j]);
for(int i=1,l,r,k;i<=n;i++){
scanf("%d%d%d",&l,&r,&k);
REF::ae(2*n+i,i,l,r,0);
REF::ae(n+i,2*n+i,l,r,0);
REF::MCMF::AE(2*n+i,REF::O,k);
}
for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){
if(c[i][j]==-1){
id[i][j]=REF::MCMF::cnt;
REF::ae(i,n+j,a[i][j],a[i][j],0);
continue;
}
if(a[i][j]){
REF::ae(i,n+j,1,1,0);
id[i][j]=REF::MCMF::cnt;
REF::ae(n+j,i,0,1,c[i][j]);
}else id[i][j]=REF::MCMF::cnt,REF::ae(i,n+j,0,1,c[i][j]);
}
REF::func();
printf("%d\n",REF::MCMF::cost);
for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)printf("%d ",REF::MCMF::edge[id[i][j]^1].val^a[i][j]);puts("");}
return 0;
}
CVI.[八省联考2018]劈配
CXXIV.CF724E Goods transportation
继续模拟网络流。
首先,一个最大流的模型是显然的:源点向每个点连边,每个点向之后的点连边,每个点再向汇点连边。但是显然这么做复杂度会炸。
考虑将最大流转为最小割。我们考虑手动分配一个点是割掉源点边还是汇点边。假如割掉汇点边,显然其费用就是 \(b_i\),即汇点流量;假如割掉源点边,则费用是在源点流量 \(a_i\) 的基础上,还要割掉每一条连到该点的边。假如到 \(i\) 为止共有 \(j\) 个点被割掉了源点边(包括 \(i\)),则剩余的 \(i-j\) 个点到 \(i\) 的边也必须被割掉,于是这时的代价就是 \(a_i+m(i-j)\),其中 \(m\) 是边权。因为状态仅与 \(i,j\) 有关,所以直接DP即可。时间复杂度 \(O(n^2)\)。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,m;
ll f[2][10100],a[10100],b[10100],res=0x3f3f3f3f3f3f3f3f;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++)scanf("%d",&b[i]);
memset(f,0x3f,sizeof(f)),f[0][0]=0;
for(int i=1;i<=n;i++){
memset(f[i&1],0x3f,sizeof(f[i&1]));
for(int j=0;j<=n;j++){
if(j)f[i&1][j]=min(f[i&1][j],f[!(i&1)][j-1]+a[i]+1ll*m*(i-j));
f[i&1][j]=min(f[i&1][j],f[!(i&1)][j]+b[i]);
}
}
for(int i=0;i<=n;i++)res=min(res,f[n&1][i]);
printf("%lld\n",res);
return 0;
}
还可以优化。考虑初始令全部点都断去源点边,仅保留汇点边。然后,考虑每次将一个点的汇点边断开,源点边连上。
显然,当我们翻转第一个点的时候,若其位置是 \(i\),则额外代价为 \(b_i-a_i+m(n-i)\),因为其与后缀所有节点间连边皆须断开。
当我们翻转第二个点(设为 \(j\))时,我们发现其额外代价为 \(b_j-a_j+m(n-j)-m\),因为边 \((i,j)\) 在 \(i,j\) 之一处被计算了,但实际上其不应考虑,故应该减去。
然后,第三个点的额外代价为 \(b_k-a_k+m(n-k)-2m\)。通过找规律,我们发现若第 \(i\) 个位置翻转了位置 \(j\),其代价为 \(b_j-a_j+m(n-j)-(i-1)m\)。
因为 \(i,j\) 代价独立,所以我们可以分开考虑。对于 \(j\) 这维,我们可以贪心地依次选取 \(b_j-a_j+m(n-j)\) 最小的,那么就将所有东西关于该值排序。之后枚举 \(i\) 即可。
(如果 \(n\) 出到 \(10^6\) 大概就可以当NOID1T2难度的题了)
时间复杂度 \(O(n\log n)\)。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,m,a[10100],b[10100];
ll o[10100],res,sum;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&a[i]),res+=a[i];
for(int i=1;i<=n;i++)scanf("%d",&b[i]),o[i]=1ll*m*(n-i)+b[i]-a[i];
sort(o+1,o+n+1),sum=res;
for(int i=1;i<=n;i++)res=min(res,sum+=o[i]-1ll*m*(i-1));
printf("%lld\n",res);
return 0;
}
CXXVI.LOJ#6405. 「ICPC World Finals 2018」征服世界
依旧把“军队”叫做老鼠,“目的地”叫做洞。
其实在模拟费用流的题中还是比较套路的(
我们考虑在每个节点上开两个小根堆维护所有的老鼠和洞。众所周知的是,位置 \(x\) 与 \(y\) 之间路径长度是 \(dis=dep_x+dep_y-2dep_{lca}\)。于是我们考虑在一个点 \(x\) 处合并子树中的路径。注意到路径的两个端点可以来自于 \(x\) 的同一个儿子,因为这样就相当于多往 \(x\) 绕了一圈,不如不绕。
在合并 \(x,y\) 后,往 \(x\) 堆中扔 \(dep_x-dis\),\(y\) 堆中扔 \(dep_y-dis\),表示反悔。同时,为了强制所有的洞都被匹配,我们预先令所有的 \(dep_y\) 全部减去一个 \(\infty\),最后再加上即可。
合并当前节点与子树的堆可以使用启发式合并,或者使用可并堆虽然我不会。
前者时间复杂度 \(O(n\log^2n)\),后者一个 \(\log\)。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n,head[250100],cnt,a[250100],b[250100];
ll dep[250100],res;
struct edge{int to,next,val;}edge[500100];
void ae(int u,int v,int w){
edge[cnt].next=head[u],edge[cnt].to=v,edge[cnt].val=w,head[u]=cnt++;
edge[cnt].next=head[v],edge[cnt].to=u,edge[cnt].val=w,head[v]=cnt++;
}
struct dat{ll v;mutable int t;dat(ll V,int T){v=V,t=T;}friend bool operator<(const dat&x,const dat&y){return x.v>y.v;}};
void merge(priority_queue<dat>&p,priority_queue<dat>&q){
if(p.size()<q.size())swap(p,q);
while(!q.empty())p.push(q.top()),q.pop();
}
priority_queue<dat>p[250100],q[250100];
void dfs(int x,int fa){
if(a[x])p[x].emplace(dep[x],a[x]);
if(b[x])q[x].emplace(dep[x]-0x3f3f3f3f3f3f,b[x]);
for(int i=head[x],y;i!=-1;i=edge[i].next){
if((y=edge[i].to)==fa)continue;
dep[y]=dep[x]+edge[i].val,dfs(y,x);
merge(p[x],p[y]);
merge(q[x],q[y]);
}
while(!p[x].empty()&&!q[x].empty()){
ll X=p[x].top().v,Y=q[x].top().v;
ll val=X+Y-2*dep[x];
if(val>=0)break;
int mn=min(p[x].top().t,q[x].top().t);
res+=val*mn;
p[x].emplace(X-val,mn);
q[x].emplace(Y-val,mn);
if(!(p[x].top().t-=mn))p[x].pop();
if(!(q[x].top().t-=mn))q[x].pop();
}
}
int main(){
scanf("%d",&n),memset(head,-1,sizeof(head));
for(int i=1,x,y,z;i<n;i++)scanf("%d%d%d",&x,&y,&z),ae(x,y,z);
for(int i=1;i<=n;i++){
scanf("%d%d",&a[i],&b[i]);
if(a[i]>=b[i])a[i]-=b[i],b[i]=0;else b[i]-=a[i],a[i]=0;
res+=0x3f3f3f3f3f3f*b[i];
}
dfs(1,0),printf("%lld\n",res);
return 0;
}