LCT。
I.LCT可以干什么?
动态树问题,
是近几年在OI中兴起的一种新型问题,
是一类要求维护一个有根树森林,
支持对树的分割,合并等操作的问题。
由Robert E Tarjan为首的科学家们
提出解决算法Link-Cut Tree,简称LCT。
——《百度百科》
算了,看看就行。
我们唯一知道的就是,你们的大毒瘤,那个发明强连通分量算法、HLPP、splay、离线LCA算法的Tarjan,他又跑来祸害咱们了!
附上高清大图

通俗点说,它支持你将一棵树一刀两断,也支持你把两棵树嫁接在一起(无性生殖?),还支持你从树上扯下来一条路径在上面搞事情。
或者换句话说,它就是(动态树剖+并查集+平衡树),再加上一堆奇妙的特性。
这么酷炫的吗!!!
好的那我们就开始吧。
II.前置芝士
splay:必修,特别是区间操作(fhq treap亦可)
树剖:选修
并查集:必修
线段树:必修
III.思想
我们常说的树链剖分,实际上是重链剖分。它还有两个兄弟,长链剖分与实链剖分。
这仨家伙有一个共同点:毒瘤可以把一棵树按照一些规则剁成几条不相交的路径。并且,这些路径上的点按照深度递增,不存在两个相同深度的点处在同一条路径上。
例如重链剖分,就是每个点和它所有子节点中\(size\)最大的点在同一条链上。
而长链剖分,我没学过,咱也不敢瞎说
LCT运用的就是里面最灵活的实链剖分。我们常见的重链剖分,一旦剖分完成,是不可以再改变链的构成的,除非你暴力重构树。
但是,实链剖分,你就可以任意指定一个点的实边和实儿子。当然咯,这么方便也不是没有坏处,在极端情况下,实链剖分是\(O(n)\)的,不像重链剖分是严格的\(O(\log n)\)。
因此,我们就将实链剖分和灵活的splay结合在一起,得到了均摊\(O(\log)\)的LCT。
我们将每一条实链,扔进一颗splay中维护。这棵splay以深度为键值,深度越大排名越靠后。
当然咯,因为splay的结构,我们没有必要建出一棵一棵的splay出来。它还是可以保有一个完整的结构的。只不过,对于某棵splay的树根,它有一个父亲,那是原树中它的父亲;但是它的父亲尽管有这个儿子,但它却不认!
例如这个剖分:
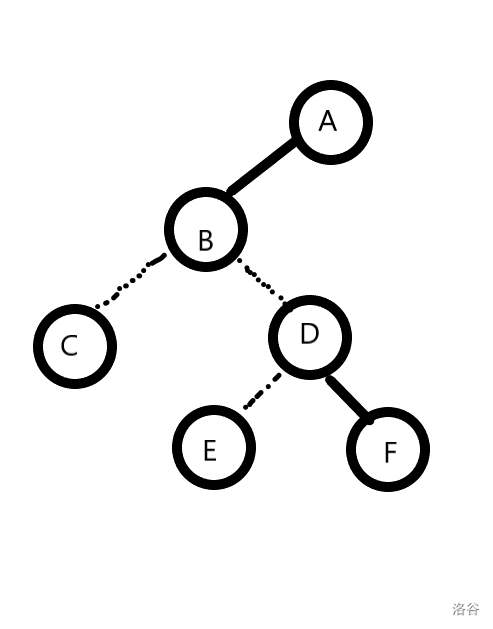
在以\(E\)为根的那棵splay中,\(E\)认了一个父亲,\(D\)。但是,\(D\)却不认\(E\)这个儿子。它唯一承认的儿子,是\(F\),它splay中的右儿子。当然,\(F\)也承认\(D\)这个父亲。
但是,splay不一定只有一种构造。也有可能,\(F\)是splay的根,而\(D\)是它的左儿子。这个时候,\(D\)和\(F\)仍然互相承认,\(D\)还是不承认\(E\),但是\(E\)承认\(D\)。
因此,我们可以看出,不管哪个儿子,都是承认与父亲的关系的。但是,父亲只承认与实儿子的关系(尽管这个实儿子有可能在splay中成为了它的父亲甚至有可能离他很远很远)。
因此我们便解锁了LCT中一个最重要的性质:实边认父也认子,虚边认父不认子。
IV.约定
\(ch\):儿子,默认为\(x\)的。\(ch_0\)为左儿子,\(ch_1\)为右儿子。
\(fa\):父亲,默认为\(x\)的。
\(root\):\(x\)所在的splay的根。
\(ROOT\):\(x\)所在的原树的根(注意区分!!!)。
V.实现
\(access(x)\)
效果:将节点\(x\)到\(ROOT\)这条路径上的所有边设成实边(并自动把其他边设成虚边),并且扔到一个splay里面。
例:

怎么实现呢?
这个时候,我们就要回想起splay的经典操作\(splay\):将一个\(x\)旋转到它所在的\(splay\)的\(root\)。
这个时候,我们就可以向\(fa\)转移了(因为\(x\)是\(root\),它的父亲一定处在不同的splay中)。
因为\(x\)的深度一定大于\(fa\)的深度,所以如果我们将\(fa\)也splay到它所属的splay的根,则\(x\)可以直接设成\(fa\)的右儿子(在设的同时,\(fa\)原本的右儿子,原来是实儿子,被直接断成了虚儿子,认父不认子,成了家庭餐具了;反而,原来认子不认父的\(x\),现在\(fa\)重新承认了\(x\)这个儿子,当然\(x\)也一直承认着\(fa\),因此这便成为了新的实边)。
看一下代码:
inline void access(int x){
for(register int y=0;x;x=t[y=x].fa)
splay(x),rson=y,pushup(x);
}
就是将\(x\)转到根;将\(x\)的右儿子设成\(y\);将\(x\)变成新的\(y\)(在\(x\)的父亲\(splay\)时继续更新)。
至于这个\(pushup\),是更新的函数,类似于线段树的\(pushup\)。
\(makeroot(x)\)
效果:将\(x\)设为这棵树的\(ROOT\)(注意不是splay的\(root\))!
先上代码:
inline void makeroot(int x){
access(x),splay(x),REV(x);
}
\(access(x)\),将\(x-ROOT\)这条路径上的点打包成一个splay;
\(splay(x)\),将\(x\)设成这个\(splay\)的根。
但是,注意,因为\(x\)在整棵\(splay\)中深度最大,它此时并没有右儿子!
因此,在调用\(REV\)函数后,整棵splay翻转过来,\(x\)成为深度最浅的那一个!
因为这棵splay中深度最浅的是根节点,所以这个时候,\(x\)就成为了新根。
\(findroot(x)\)
效果:将\(x\)到\(ROOT\)的路径打包成一个splay,找到\(x\)的\(ROOT\),并将\(ROOT\)转到\(root\)。
先上代码:
inline int findroot(int x){
access(x),splay(x);
while(lson)pushdown(x),x=lson;
splay(x);
return x;
}
可以类比冰茶姬的找父亲操作。
\(access\)函数打包,\(splay\)函数转到\(root\),那个\(while\)循环找到深度最浅的点,即为\(ROOT\),再\(splay\)就把\(ROOT\)转到\(root\)(保证深度为\(\log\)级别),并返回\(root\)。
如果你把这些函数的目的都能想清楚,就没有问题了。
\(split(x,y)\)
效果:将\(x\)到\(y\)路径上的所有点打包成一个splay,并令\(y\)为\(root\)。
代码:
inline bool split(int x,int y){
if(findroot(x)!=findroot(y))return false;
makeroot(x),access(y),splay(y);
return true;
}
如果\(x\)和\(y\)不在同一颗树中,显然操作不合法,直接退出;
否则,把\(x\)设成新\(ROOT\),这样子再\(access\)一下就抽出了\(ROOT-y\)的路径。由于\(x\)就是\(ROOT\),这就是\(x\)到\(y\)的路径。然后再将\(y\) \(splay\)到\(root\),保证深度。
\(link(x,y)\)
效果:在节点\(x,y\)间连一条边。
代码:
inline bool link(int x,int y){
makeroot(x);
if(findroot(y)==x)return false;
t[x].fa=y;
return true;
}
把\(x\)转到\(ROOT\);如果发现\(x,y\)已经连通(在同一棵子树中),忽略之;否则,将\(x\)的父亲设成\(y\),相当于连一条虚边。
\(cut(x,y)\)
效果:断掉节点\(x,y\)间的边。
代码:
inline bool cut(int x,int y){
makeroot(x);
if(findroot(y)!=x||t[y].fa!=x||t[y].ch[0])return false;
t[x].ch[1]=t[y].fa=0;
pushup(x);
return true;
}
这是仅次于\(access\)最重点的一个,也是仅次于\(access\)最难的那个。
先让\(x\)为\(ROOT\);如果\(findroot(y)\neq x\),即它们不在同一棵树中,忽略之;如果\(t[y].fa\neq x\),则显然它们之间不可能有边,因为\(findroot\)后,\(x\)和\(y\)处于同一棵splay中,且\(x\)是根(不明白的马上转回去看\(findroot\)),则深度差为\(1\)的点对\((x,y)\)必然紧贴;就算这两点都满足,如果\(y\)有左儿子,则\(x\)和\(y\)仍然没有真正地紧贴,它们之间也不可能有边;这些都是需要忽略的。
之后,就是断边了。因为这时\(x\)为根,且\(x\)的深度小于\(y\),因此\(x\)的右儿子一定就是\(y\)。
VI.汇总
struct LCT{
int fa,ch[2],val,sum;
bool rev;
}t[100100];
inline int identify(int x){
if(x==t[t[x].fa].ch[0])return 0;
if(x==t[t[x].fa].ch[1])return 1;
return -1;
}
inline void pushup(int x){
t[x].sum=t[lson].sum^t[rson].sum^t[x].val;
}
inline void REV(int x){
t[x].rev^=1,swap(t[x].ch[0],t[x].ch[1]);
}
inline void pushdown(int x){
if(!t[x].rev)return;
if(lson)REV(lson);
if(rson)REV(rson);
t[x].rev=0;
}
inline void rotate(int x){
register int y=t[x].fa;
register int z=t[y].fa;
register int dirx=identify(x);
register int diry=identify(y);
register int b=t[x].ch[!dirx];
if(diry!=-1)t[z].ch[diry]=x;t[x].fa=z;
if(b)t[b].fa=y;t[y].ch[dirx]=b;
t[y].fa=x,t[x].ch[!dirx]=y;
pushup(y),pushup(x);
}
inline void pushall(int x){//pushdown the nodes in the route from x to root
if(identify(x)!=-1)pushall(t[x].fa);
pushdown(x);
}
inline void splay(int x){//splay x to the root
pushall(x);
while(identify(x)!=-1){
register int fa=t[x].fa;
if(identify(fa)==-1)rotate(x);
else if(identify(x)==identify(fa))rotate(fa),rotate(x);
else rotate(x),rotate(x);
}
}
inline void access(int x){//pull out all the nodes in the route from x to the ROOT, and form a splay
for(register int y=0;x;x=t[y=x].fa)splay(x),rson=y,pushup(x);
}
inline void makeroot(int x){//make x the new ROOT
access(x),splay(x),REV(x);
}
inline int findroot(int x){//find the ROOT of x, and make ROOT the root
access(x),splay(x);
while(lson)pushdown(x),x=lson;
splay(x);
return x;
}
inline bool split(int x,int y){//pull out the route from x to y and form a splay rooted y; if there isn't such route,return false
if(findroot(x)!=findroot(y))return false;
makeroot(x),access(y),splay(y);
return true;
}
inline bool link(int x,int y){//link an edge between x and y; if they have already connected before, return false.
makeroot(x);
if(findroot(y)==x)return false;
t[x].fa=y;
return true;
}
inline bool cut(int x,int y){//cut the edge between x and y; if there isn't such edge, return false
makeroot(x);
if(findroot(y)!=x||t[y].fa!=x||t[y].ch[0])return false;
t[x].ch[1]=t[y].fa=0;
pushup(x);
return true;
}
注意到几处与普通splay的不同:
1.在\(identify\)函数判断左儿子还是右儿子时,如果\(return -1\),则说明\(x\)是\(root\)。
2.在\(splay\)时调用\(pushall\)函数,从上到下递归地\(pushdown\)。
3.在\(rotate\)时,在多个可能为\(root\)或者该节点不存在的地方进行特判。
I.【模板】Link Cut Tree (动态树)
直接把那份模板加个头尾就能过。