Manacher=马拉车
大家好,我们今天来扯Manacher算法了。
I.马拉车可以干什么?
一句话:对于一个字符串(s),在(O(|S|))时间内,求出它的最长回文子串。
II.预处理
对于一个字符串,它的回文串可以有两种类型:
A.奇回文串
例:AACCBCCAA
特征:有单一回文中心(例中的B)。
B.偶回文串
例:AABBCCBBAA
特征:对称中心是两个(例中的BB)。
两者性质并不相同,必须分类讨论。
但是,我们有一种方法,可以将两者统一成一种类型:
在原串每两个字符之间,以及串头串尾,都加上一个无关字符(例如 # 等)。
例:
AABBCCDD( ightarrow) #A#A#B#B#C#C#D#D#。
ABCBA( ightarrow) #A#B#C#B#A#。
这样的话,原串中的奇回文串与偶回文串,都被统一成了奇回文串。(奇回文串变成以原串字符为对称中心的回文串,偶回文串变成以 # 为对称中心的回文串)。
代码(在读入时直接进行操作):
inline void getln(){
s[0]='$',S=1;
char c=getchar();
while(c>'z'||c<'a')c=getchar();
while(c>='a'&&c<='z')s[S++]=c,s[S++]='$',c=getchar();
s[S]='�';
}
III.主算法
(默认字符串从(0)开始)
(暂时忽略添加进来的 # 字符,因为忽略也无影响)
先考虑暴力思路:枚举对称中心,然后枚举对称半径。总复杂度(O(n^2))。
(当然,可以哈希+二分达到(O(nlog_2n)),但是这个思路对我们没有帮助)
同kmp算法一样,我们可以思考一些操作来避免重复枚举。
这时候我们就可以设两个变量:
(Rpos):在沿着(s)顺序匹配时,当前所有出现过的回文串中,它的右边界达到的最右位置。
例:ABABAAC,在位置(3)时,(Rpos=4)。在位置(2)和(3)的回文串都曾达到这里。
(Centre):对于当前的(Rpos),它所对应的对称中心。如果有多个,取最左端的一个。
例:ABABAAC,在位置(3)时,(Centre=2)。在位置(2)和(3)的回文串都曾达到(Rpos),但是(2)是最左端的一个。
我们再设一个数组(rad),表示位置(i)时的回文半径。
| 字母 | A | B | A | B | A | A | C |
|---|---|---|---|---|---|---|---|
| (rad_i) | 1 | 2 | 3 | 2 | 1 | 1 | 1 |
(自动忽略了偶回文串)。
接下来我们就开始操作了。
初始令(Rpos=Centre=-1)。
对于当前位置(i):
1. (i geq Rpos)
暴力延伸,这里是未涉及到的新地方。
2. (i < Rpos)
这时,我们令(ref)为(i)关于(Centre)的对称点(即(Centre*2-i))。
同时令(Lpos)为(Rpos)关于(Centre)的对称点。
再令(lp)为以(ref)为对称中心的回文串的左边界。
2.1. (Lpos<lp)
因为是回文串,所以有(s_{Lpos}...s_{Centre}=s_{Rpos}...s_{Centre})
则关于(ref)对称的回文串,也是关于(i)对称的回文串(想一想,左右对称)。
如图:
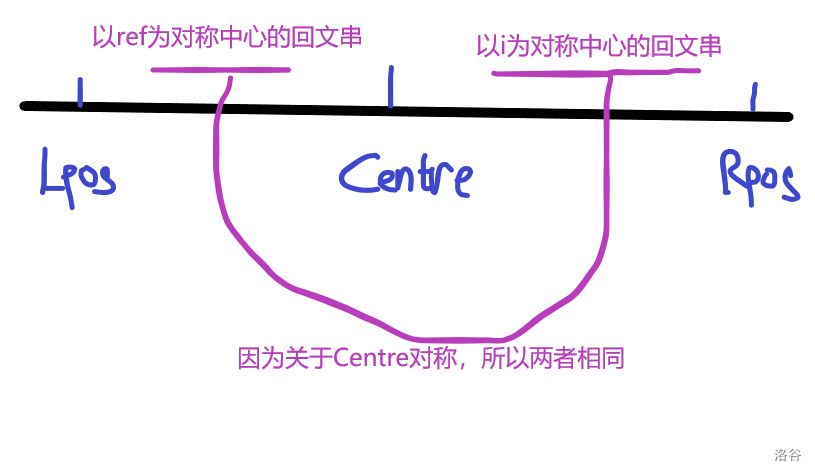
2.2. (Lposgeq lp)
对称的只有从(i)到(Rpos)的一段,剩下的部分两边是不同的,仍需暴力扩展。
如图:
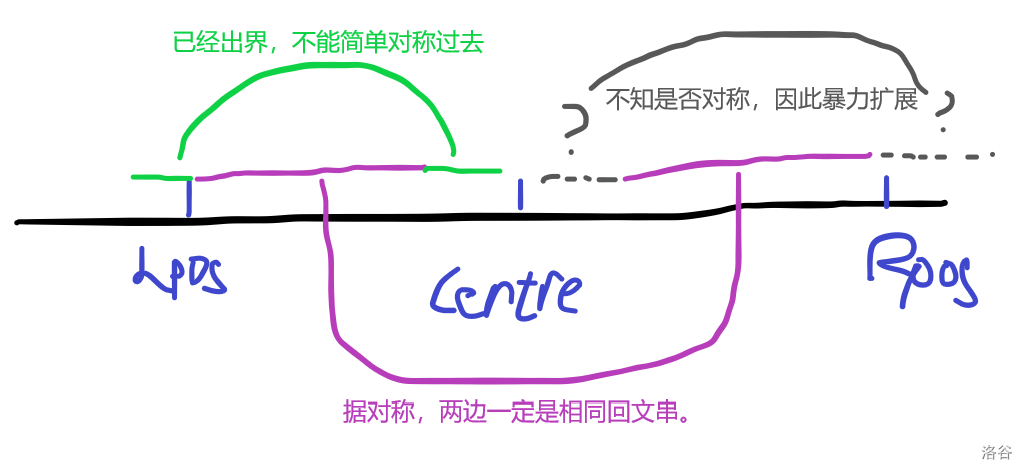
IV.实现
inline void Manacher(){
Centre=Rpos=-1;
for(register int i=0;i<S;i++){
rad[i]=(i<Rpos)?min(Rpos-i,rad[Centre*2-i]):1;
while(i+rad[i]<S&&i-rad[i]>=0)if(s[i+rad[i]]==s[i-rad[i]])rad[i]++;else break;
if(i+rad[i]>Rpos)Rpos=i+rad[i],Centre=i;
Ans=max(Ans,rad[i]);
}
}
实现与上面的描述很不一致,我们逐行分析。
rad[i]=(i<Rpos)?min(Rpos-i,rad[Centre*2-i]):1;
用了三目运算符。
它的意思是:
如果(i<Rpos),那么(rad_i=min(Rpos-i,rad_{Centre*2-i})
回忆一下,(ref)就是(Centre*2-i)。
(Rpos-i),就是上文(2.2)中的可用部分。
(rad_{Centre*2-i}),就是上文(2.1)中的可用部分。
两者取(min),就很显然了。
而当(i geq Rpos)时,(rad_i=1)(默认单个字符本身就为回文串)。
然后就是暴力跳了。
while(i+rad[i]<S&&i-rad[i]>=0)if(s[i+rad[i]]==s[i-rad[i]])rad[i]++;else break;
分析一下,在情形(1)和(2.2),都需要暴力跳。在情形(2.1),暴力跳一次就会退出。
然后按定义更新(Rpos)和(Centre),同时取答案。
if(i+rad[i]>Rpos)Rpos=i+rad[i],Centre=i;
Ans=max(Ans,rad[i]);
最终答案为(Ans-1),因为在长度为(n)的原串中加入了(n+1)个 # 。但是(rad)又是半径,也要再加入(rad-1)个字符才能构成回文串。
总复杂度(O(n))。分析复杂度是不可能的,这辈子都是不可能的。
V.大礼包
本文所有代码使用的分隔符都是dollar符号,但是由于(LaTeX)的缘故,在讲解时使用 # 符号。另,还是因为(LaTeX),文中的dollar符号全部莫名其妙多了一个空格,请自行删除。
(代码:【模板】manacher算法
#pragma GCC optimise(3)
#include<bits/stdc++.h>
using namespace std;
char s[22000100];
int S,rad[22001000],Centre,Rpos,Ans;
inline void getln(){
s[0]='$',S=1;
char c=getchar();
while(c>'z'||c<'a')c=getchar();
while(c>='a'&&c<='z')s[S++]=c,s[S++]='$',c=getchar();
s[S]='�';
}
inline void Manacher(){
Centre=Rpos=-1;
for(register int i=0;i<S;i++){
rad[i]=(i<Rpos)?min(Rpos-i,rad[Centre*2-i]):1;
while(i+rad[i]<S&&i-rad[i]>=0)if(s[i+rad[i]]==s[i-rad[i]])rad[i]++;else break;
if(i+rad[i]>Rpos)Rpos=i+rad[i],Centre=i;
Ans=max(Ans,rad[i]);
}
}
int main(){
getln();
Manacher();
printf("%d
",Ans-1);
return 0;
}
(忽略上面的O3)