XII.CF827E Rusty String
依旧推式子。假设当前我们处理('V')字符,那么我们令(f(x)=[s_x='V"lor s_x='?'])。我们设答案为(p(x)),那么有(p(x)=sumlimits_{i=x}^{n-1}f(i)f(i-x))。
老套路,翻转(f)函数,得到(g)函数,即(g(x)=f(n-i-1))。我们有(p(x)=sumlimits_{i=x}^{n-1}f(i)g(n-i+x-1))。换句话说,有(p(x)=sumlimits_{i+j=n+x-1}f(i)g(j))。
我们设(h=f*g)。则有(p(x)=h(n+x-1))。
('K')字符同理。
但是,为了避免('?')匹配('?')出现两次,我们还要额外再对('?')跑一遍,就是令(f(x)=[s_x='?']),然后(p_x)减去(h(n+x-1))。
当你费尽心思搞完这一切时,却发现你的程序假掉了。这都得感谢第一组良心样例。
我们看一下:
V??VK
V??VK
其中第三个字符('?'),在上面的串中同('V')匹配,在下面的串中同('K')匹配。毕竟,这是未确定的字符,而不是通配符。未确定的字符只能是('V')或('K'),但不能同时既是('V')又是('K')。
怎么办呢???
我们引出一个性质:如果(k)是一个合法的(period),那么,所有(k)的倍数都必然是合法的(period)。
看一张图:
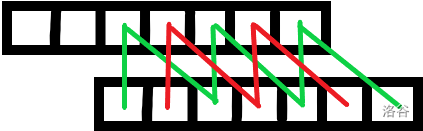
所有的红线连着的位置全都相等。所有的绿线连着的位置全部相等。换句话说,如果有一个(period)为(k),那么(forall iequiv j),总有(s_i=s_j)。这样,就必有(k)的倍数也全为循环节。
如果有一个('?')被当成了通配符的话,那么首先,必有(k<n/2),不然无法被匹配两次。这样,就肯定存在(k)的倍数。那么,在倍数中,(k)肯定匹配了不同的东西,不可能每次都匹配一样的东西。那么,这就能判断出来。
证明比较感性,理性的看不懂的证明详见CF tutorial。
代码:
#include<bits/stdc++.h>
using namespace std;
const double pi=acos(-1);
int T,n,lim=1,lg,p[1<<20],rev[1<<20],cnt;
char s[500100];
struct cp{
double x,y;
cp(double u=0,double v=0){x=u,y=v;}
friend cp operator +(const cp &u,const cp &v){return cp(u.x+v.x,u.y+v.y);}
friend cp operator -(const cp &u,const cp &v){return cp(u.x-v.x,u.y-v.y);}
friend cp operator *(const cp &u,const cp &v){return cp(u.x*v.x-u.y*v.y,u.x*v.y+u.y*v.x);}
}f[1<<20],g[1<<20];
void FFT(cp *a,int tp){
for(int i=0;i<lim;i++)if(i<rev[i])swap(a[i],a[rev[i]]);
for(int md=1;md<lim;md<<=1){
cp rt=cp(cos(pi/md),tp*sin(pi/md));
for(int stp=md<<1,pos=0;pos<lim;pos+=stp){
cp w=cp(1,0);
for(int i=0;i<md;i++,w=w*rt){
cp x=a[pos+i],y=w*a[pos+md+i];
a[pos+i]=x+y;
a[pos+md+i]=x-y;
}
}
}
}
bool ok[1<<20];
int main(){
scanf("%d",&T);
while(T--){
scanf("%d%s",&n,s),cnt=0;
lim=1,lg=0;
while(lim<=2*n)lim<<=1,lg++;
for(int i=0;i<lim;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
for(int i=0;i<lim;i++)f[i]=g[i]=cp(0,0);
for(int i=0;i<n;i++)f[i]=g[n-i-1]=cp(s[i]=='V'||s[i]=='?',0);
FFT(f,1),FFT(g,1);
for(int i=0;i<lim;i++)f[i]=f[i]*g[i];
FFT(f,-1);
for(int i=1;i<=n;i++)p[i]=(int)(f[n+i-1].x/lim+0.5);
for(int i=0;i<lim;i++)f[i]=g[i]=cp(0,0);
for(int i=0;i<n;i++)f[i]=g[n-i-1]=cp(s[i]=='K'||s[i]=='?',0);
FFT(f,1),FFT(g,1);
for(int i=0;i<lim;i++)f[i]=f[i]*g[i];
FFT(f,-1);
for(int i=1;i<=n;i++)p[i]+=(int)(f[n+i-1].x/lim+0.5);
for(int i=0;i<lim;i++)f[i]=g[i]=cp(0,0);
for(int i=0;i<n;i++)f[i]=g[n-i-1]=cp(s[i]=='?',0);
FFT(f,1),FFT(g,1);
for(int i=0;i<lim;i++)f[i]=f[i]*g[i];
FFT(f,-1);
for(int i=1;i<=n;i++)p[i]-=(int)(f[n+i-1].x/lim+0.5);
// for(int i=1;i<=n;i++)printf("%d ",p[i]);puts("");
for(int i=1;i<=n;i++)ok[i]=(p[i]==n-i);
for(int i=1;i<=n;i++)for(int j=i;j<=n;j+=i)ok[i]&=ok[j];
for(int i=1;i<=n;i++)cnt+=ok[i];
printf("%d
",cnt);
for(int i=1;i<=n;i++)if(ok[i])printf("%d ",i);puts("");
}
return 0;
}