题目:HDU 3037
题意:有n个树,m个坚果,放到n个树里,可以不放完,有多少种方法。
分析:

得到组合数了。
大组合数什么费马小定理,Lucas定理都来了;
总的说,不能用二维地推了,用的却是组合数的定义。
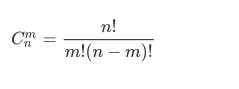
一般来说大组合通常要取模。
那么不能边乘边模,边除边模,等式不会成立。
根据逆元,除以一个数取模 = 乘以这个数对mod的逆元。
那么式子就可以写成: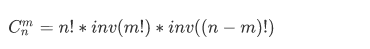
这里,我们可以预处理所有 i 对 mod 的逆元后,累乘,这样得到的就是阶乘的逆元。
然后就是求 i 对 mod 的逆元了,什么扩展欧几里得就来了。
当然,有费马小定理。
inv[i] = (mod-mod/i)*inv[mod%i]%mod;
整个求大组合数就是这样出来了。
void init() { fac[0] = 1; for(int i=1;i<maxn;i++) fac[i] = i*fac[i-1]%mod; inv[0] = inv[1] = 1; for(int i=2;i<maxn;i++) inv[i] = (ll)(mod-mod/i)*inv[mod%i]%mod; for(int i=2;i<maxn;i++) inv[i] = inv[i-1]*inv[i]%mod; } ll C(ll n,ll m) { if(n<m) return 0; return fac[n]*inv[m]%mod*inv[n-m]%mod; }
但是这个题目n,m的范围惊人1000000000,作为阶乘,逆元,数组开不下。
Lucas来了:

看结果吧:
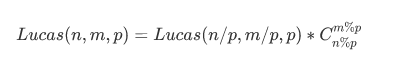
还是有组合数,用了费马定理:
fac[n]*Inv(fac[m])%P*Inv(fac[n-m])%P;
因为这里的对P的逆元 Inv已经不能用数组表示和地推了,Inv()函数,利用了费马定理,快速幂等等,原理很复杂了,哈哈~~~,我就不证明了。
void initFac(int n) { fac[0] = 1; for(int i=1;i<=n;i++) fac[i] = i*fac[i-1]%P; } ll Pow(ll a,int b) { ll re = 1; for(;b;b>>=1,a=a*a%P) if(b&1) re = re*a%P; return re; } ll Inv(ll a) { return Pow(a,P-2); } ll C(ll n,ll m) { if(n<m) return 0; return fac[n]*Inv(fac[m])%P*Inv(fac[n-m])%P; } ll Lucas(ll n,ll m) { if(n<m) return 0; ll re = 1; for(;m;n/=P,m/=P) re = re*C(n%P,m%P)%P; return re; }