数论初步

求两个数的最大公约数

1、高精度运算
2、唯一分解定理：将两个数分解为素数的 n 次方的形式，然后依次计算；
3、欧几里得算法：

1 int gcd(int a,int b) {
2     return b==0 ? a : gcd(b,a%b);
3 }

最小公倍数 = a * b / gcd(a,b)，注意精度；

ax+by+c = 0 直线上有多少个整点 (x,y) 满足 x 属于 [x1,x2]，y 属于 [y1,y2]。
这是扩展欧几里得算法：

首先解决扩展欧几里得 ax + by = gcd(a,b)，x,y为整数；

 1 void gcd(int a,int b,int& d,int& x,int& y) {
 2     if(!b) {
 3         d = a;
 4         x = 1;
 5         y = 0;
 6         // gcd(a,0) = 1*a + 0*0 = a;
 7     }
 8     else {
 9         gcd(b,a%b,d,y,x);
10         y-=x*(a/b);
11     }
12 }

找到了ax + by = gcd(a,b) 的一组解。那么其他解呢？

然后这还只是 = gcd(a,b)，当移项等于 -c 的时候情况呢？

其实可以通过上面的情况转换过来；

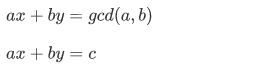
当 c 是 gcd(a,b) 的倍数的时候有解，否则无解。其中一个组解是：

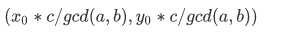
其他解：

同余与模运算：

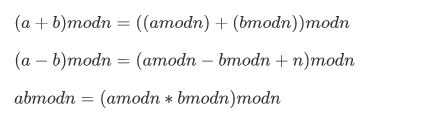
大整数取模：（就是小学生模拟除法运算）

1     scanf("%s%d",n,&m);
2     int len = strlen(n);
3     int ans = 0;
4     for(int i=0;i<len;i++) 
5         ans = (int)(((long long)ans*10 + n[i]-'0')%m);
6     printf("%d
",ans);

幂取模：（俗称快速幂，二分的思想）

1 int pow_mod(int a,int n,int m) {
2     if(n==0) return 1;
3     int x = pow_mod(a,n/2,m);
4     long long ans = (long long)x*x%m;
5     if(n%2==1) ans = ans*a%m;
6     return (int)ans;
7 }

模线性方程组：ax≡b(modn) 同余

即： ax-b = ny;扩展欧几里得求解；

筛素数：

    // 0 是 素数
    memset(vis,0,sizeof(vis));
    for(int i=2;i<=n;i++) {
        for(j=i*2;j<=n;j+=i)
            vis[j] = 1;
    }

此算法效率已经足够了；

改进：

    int m = sqrt(n+0.5);
    memset(vis,0,sizeof(vis));
    for(int i=2;i<=m;i++) {
        if(!vis[i]) {
            for(j=i*i;j<=n;j+=i)
                vis[i] = 1;
        }
    }

素数定理：

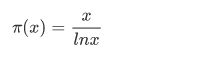
不超过 x 的素数的个数，约等于。