@description@
曾经有一款流行的游戏,叫做 Infinity Loop,先来简单的介绍一下这个游戏:
游戏在一个 n*m 的网格状棋盘上进行,其中有些小方格中会有水管,水管可能在方格某些方向的边界的中点有接口,所有水管的粗细都相同,所以如果两个相邻方格的公共边界的中点都有接头,那么可以看作这两个接头互相连接。水管有以下 15 种形状:
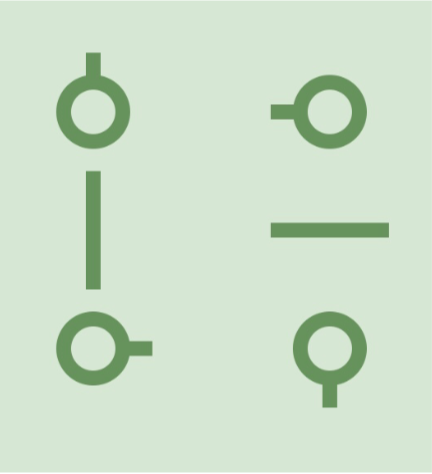

游戏开始时,棋盘中水管可能存在漏水的地方。形式化地:如果存在某个接头,没有和其它接头相连接,那么它就是一个漏水的地方。
玩家可以进行一种操作:选定一个含有非直线型水管的方格,将其中的水管绕方格中心顺时针或逆时针旋转 90 度。
直线型水管是指左图里中间一行的两种水管。
现给出一个初始局面,请问最少进行多少次操作可以使棋盘上不存在漏水的地方。
@solution@
发现数据范围没办法用插头 dp,但是数据范围又比较小,而且是网格图中相邻格子关系类型的题。尝试用网络流。
首先判定合法性。我们对格子黑白染色,黑格外流,白格内流。
1)如果一个格子的插头数为 0, 1, 3, 4,则它的形状只受它的插头数影响。
我们可以直接用源汇点与该格子连容量为插头数的边,然后把该格子连向四连通的格子。
2)如果一个格子的插头数为 2,则它可能为折线型/直线型。
直线型格子依然可以直接用源汇点与该格子连容量为插头数的边,不过连接时只能连两个方向。
折线型则需要拆点,拆成一个横点和一个纵点。横点容量为 1,连上下方向;纵点容量为 1,连左右方向。
最后满流即合法。
然后是最小代价。边容量与上面一样,我们考虑相邻两个格子连接的边的费用。而这条边的费用可以看成两个点分别贡献的费用之和。
1)如果某格子插头数为 0, 4 或 2 直线型,则它连相邻格子的边中贡献为 0。
2)如果某格子插头数为 1,它初始方向贡献为 0,背对初始方向为 2,其他方向为 1。
3)如果某格子插头数为 2 折线型,分横纵两点,横/纵点初始方向为 0,背对初始方向为 1。
4)如果某格子插头数为 3。先给答案加一(避免分数)。初始的凸起朝向为 -1,背对初始凸起朝向为 1,其他方向为 0。
@accepted code@
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 2000;
namespace FlowGraph{
const int MAXV = 2*MAXN + 10, MAXE = 100*MAXV, INF = (1 << 30);
struct edge{
int to, cap, flow, cost;
edge *nxt, *rev;
}edges[MAXE + 5], *adj[MAXV + 5], *cur[MAXV + 5], *ecnt = edges;
int d[MAXV + 5], h[MAXV + 5], n, s, t;
void addedge(int u, int v, int c, int w) {
edge *p = (++ecnt), *q = (++ecnt);
(*p) = (edge){v, c, 0, w, adj[u], q}; adj[u] = p;
(*q) = (edge){u, 0, 0, -w, adj[v], p}; adj[v] = q;
// printf("! %d %d %d %d
", u, v, c, w);
}
int f[MAXV + 5], hp[MAXV + 5];
void update(int x, int k) {
f[x] = k;
while( x ) {
hp[x] = x;
if( (x<<1) <= n && f[hp[x<<1]] < f[hp[x]] )
hp[x] = hp[x<<1];
if( (x<<1|1) <= n && f[hp[x<<1|1]] < f[hp[x]] )
hp[x] = hp[x<<1|1];
x >>= 1;
}
}
bool relabel() {
for(int i=1;i<=n;i++)
h[i] += d[i], f[i] = d[i] = INF, cur[i] = adj[i], hp[i] = i;
update(t, d[t] = 0);
while( f[hp[1]] != INF ) {
int x = hp[1]; update(x, INF);
for(edge *p=adj[x];p;p=p->nxt) {
int c = p->rev->cost + h[x] - h[p->to];
if( p->rev->cap > p->rev->flow && d[p->to] > d[x] + c )
update(p->to, d[p->to] = d[x] + c);
}
}
return d[s] != INF;
}
bool vis[MAXV + 5];
int aug(int x, int tot) {
if( x == t ) return tot;
vis[x] = true; int sum = 0;
for(edge *&p=cur[x];p;p=p->nxt) {
int c = p->cost + h[p->to] - h[x];
if( d[x] == d[p->to] + c && !vis[p->to] && p->cap > p->flow ) {
int del = aug(p->to, min(tot - sum, p->cap - p->flow));
sum += del, p->flow += del, p->rev->flow -= del;
if( sum == tot ) break;
}
}
vis[x] = false; return sum;
}
int min_cost_max_flow(int _s, int _t) {
int cost = 0; s = _s, t = _t;
while( relabel() )
cost += (d[s] + h[s]) * aug(s, INF);
return cost;
}
}
const int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};
int id[4][MAXN + 5][MAXN + 5], c[4][MAXN + 5][MAXN + 5];
int main() {
int n, m; scanf("%d%d", &n, &m);
int cnt = 0, s = (++cnt), t = (++cnt), ans = 0;
for(int i=1;i<=n;i++)
for(int j=1,x,tot;j<=m;j++) {
scanf("%d", &x), tot = 0;
for(int o=0;o<4;o++)
if( (x >> o) & 1 ) tot++;
if( tot == 2 ) {
if( x == 5 || x == 10 ) {
int p = (++cnt);
if( (i + j) & 1 ) FlowGraph::addedge(s, p, tot, 0);
else FlowGraph::addedge(p, t, tot, 0);
id[x == 5 ? 0 : 1][i][j] = id[x == 5 ? 2 : 3][i][j] = p;
} else {
int p = (++cnt), q = (++cnt);
if( (i + j) & 1 ) FlowGraph::addedge(s, p, 1, 0), FlowGraph::addedge(s, q, 1, 0);
else FlowGraph::addedge(p, t, 1, 0), FlowGraph::addedge(q, t, 1, 0);
id[0][i][j] = id[2][i][j] = p, id[1][i][j] = id[3][i][j] = q;
for(int o=0;o<4;o++) c[o][i][j] = !((x >> o) & 1);
}
} else if( tot != 0 ) {
int p = (++cnt);
if( (i + j) & 1 ) FlowGraph::addedge(s, p, tot, 0);
else FlowGraph::addedge(p, t, tot, 0);
for(int o=0;o<4;o++) id[o][i][j] = p;
if( tot == 1 ) {
for(int o=0;o<4;o++)
if( (x >> o) & 1 ) {
c[o][i][j] = 0, c[(o + 2) % 4][i][j] = 2;
c[(o + 1) % 4][i][j] = c[(o + 3) % 4][i][j] = 1;
}
} else if( tot == 3 ) {
for(int o=0;o<4;o++)
if( !((x >> o) & 1) ) {
c[o][i][j] = 1, c[(o + 2) % 4][i][j] = -1;
c[(o + 1) % 4][i][j] = c[(o + 3) % 4][i][j] = 0;
}
ans++;
}
}
}
/*
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) {
for(int o=0;o<4;o++)
printf("(%2d, %2d) ", id[o][i][j], c[o][i][j]);
puts("");
}
*/
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if( (i + j) & 1 ) {
for(int o1=0;o1<4;o1++) {
int x = i + dx[o1], y = j + dy[o1], o2 = (o1 + 2) % 4;
if( id[o1][i][j] && id[o2][x][y] )
FlowGraph::addedge(id[o1][i][j], id[o2][x][y], 1, c[o1][i][j] + c[o2][x][y]);
}
}
FlowGraph::n = cnt; ans += FlowGraph::min_cost_max_flow(s, t);
for(FlowGraph::edge *p=FlowGraph::adj[s];p;p=p->nxt) {
if( p->flow != p->cap ) {
puts("-1");
return 0;
}
}
for(FlowGraph::edge *p=FlowGraph::adj[t];p;p=p->nxt) {
if( p->rev->flow != p->rev->cap ) {
puts("-1");
return 0;
}
}
printf("%d
", ans);
}
@details@
其实基本思路比较简单清晰,只是需要大力讨论。
想清楚了写,自然就可以一遍 AC 了。