(1)模板表头
//所有模板默认 prime[],powe[]从下标0开始取
const int MAXL = 1e6+7;
int phi[MAXL];//欧拉函数 int tot; int prim[MAXL];//素数表 int cnt; int vis[MAXL];
int powe[MAXL];//质数幂
int cur;
(1*)全部头文件

#include <algorithm> #include <iostream> #include <cstdio> #include <cstring> #include <string> #include <cmath> #include <vector> #include <stack> #include <queue> #include <set> #include <map> #include <complex> #define IOS ios::sync_with_stdio(0); cin.tie(0); #define mp make_pair #define Accept 0 using namespace std; typedef long long ll; typedef unsigned long long ull; typedef pair<int, int> pii; const double Pi = acos(-1.0); const double esp = 1e-9; const int inf = 0x3f3f3f3f; const int maxn = 1e5+7; const int maxm = 1e6+7; const int mod = 1e9+7; //所有模板默认 prime[],powe[]从下标0开始取 const int MAXL = 1e6+7; int phi[MAXL];//欧拉函数 int tot; int prim[MAXL];//素数表 int cnt; int vis[MAXL]; int powe[MAXL];//质数幂 int cur;
(1)素数筛
<1>暴力判断:O(n*sqrt(n))

bool isprime(int n) { int i; for(i=2;i<=sqrt(n);i++) if(n%i==0) return false; return true; }
<2>埃拉托斯特尼筛O(nlog^logn)

int vis[MAXL]; int prim[MAXL]; //返回打出的素数个数 int getPrime(){ memset(vis,0,sizeof(vis)); memset(prim,0,sizeof(prim)); int cnt=0; //打出MAXL 以内的素数表 vis[0]=vis[1]=1; int m = sqrt(MAXL); for(int i = 2; i < m ;i++) if(!vis[i]) for(int j = i*i; j < MAXL;j+=i) vis[j] = 1; for(int k=0;k<MAXL;k++) if(!vis[k]) prim[cnt++]=k; return cnt; }
<3>欧拉筛(线性)O(N)

int getPrime(){ int i ,j; int cnt = 0; memset(vis,0,sizeof(0)); vis[0] = vis[1] = 1; for(i=2;i<=MAXL;++i) { if(!vis[i]) vis[i]= prim[cnt++]= i; for(j=0;j<cnt&&i*prim[j]<=MAXL;++j){ vis[i*prim[j]] = 1; if(i%prim[j]==0) break; } } return cnt; }
(1)唯一分解定理(求分解数组powe)

int getPower(ll n,int cnt){ memset(powe,0,sizeof(powe));//cnt为prime最大下标(以免越界) int cur = 0;//cur的下标与素数表的下标相同 for(int i = 0; i < cnt ; i++)//i为素数的下表 { if(n==1) break; while(n%prim[i]==0){ powe[cur]++; n/=prim[i]; } cur++; }return cur;//powe最大素数下标 }
(1*)唯一分解定理常用(优化)

int getPower(ll n,int cnt){ //直接用下标表示质因子值 memset(powe,0,sizeof(powe));//cnt为prime最大下标(以免越界) int cur = 0; for(int i = 0; (ll)prim[i]*prim[i]<=n && i<cnt ; i++) { while(n%prim[i]==0){ powe[prim[i]]++; n /= prim[i]; } cur = prim[i]; } if(n>1) { powe[n]++; return n;//返回最大质因子下标 }else { return cur; } }
(2)欧拉函数
<1>单个求

int getPhi(int x){ int ans = x; for(int i = 2; i*i <= x; i++){ if(x % i == 0){ ans = ans / i * (i-1); while(x % i == 0) x /= i; } } if(x > 1) ans = ans / x * (x-1); return ans; }
<2>线性打表+(打prime表)

void eulerPhi(){ tot = 0; memset(phi,0,sizeof(phi)); phi[1] = 1; for(int i = 2; i < MAXL; i ++){ if(!phi[i]){ phi[i] = i-1; prim[tot ++] = i; } for(int j = 0; j < tot && 1ll*i*prim[j] < MAXL; j ++){ if(i % prim[j]) phi[i * prim[j]] = phi[i] * (prim[j]-1); else{ phi[i * prim[j]] = phi[i] * prim[j]; break; } } } }
(3)快速幂

ll quickPow(ll a, ll b){ int ans = 1; a = a % mod; while(b){ if(b&1)ans = (ans * a) % mod; a = (a * a) % mod; b >>= 1; } return ans%mod; }
(4)GCD
<0>gcd(a,b) 与 lcm(a,b) 与唯一分解定理

已知 a=p1^n1 * p2^n2 * p3^n3... b=p1^m1 * p2^m2 * p3^m3... (a,b)=p1^min(n1,m1) * p2^min(n2,m2) * p3^min(n3,m3)... [a,b]=p1^max(n1,m1) * p2^max(n2,m2) * p3^max(n3,m3)...
<0>gcd 与 lcm
lcm = gcd * (a / gcd) * (b / gcd)
<1>gcd

ll gcd(ll a,ll b){ return b?gcd(b,a%b):a; }
<2>exgcd(最小正整数解,求逆元)
下面两式子相等 ax+ by= c 方程最小正整数解( p=exgcd(a,b),if(c%p==0)有解 else 无解; ) ax≡b(mod n) 求逆元原理(同余方程)
ax+by=gcd(a,b) (a,b互质才有解)//该模板

ll exgcd(ll a, ll b, ll &x, ll &y) { if(b == 0) { x = 1; y = 0; return a; } ll d = exgcd(b,a%b,x,y),temp = x; x = y; y = temp-a/b*y; return d; }
(5)约数
<1>约数个数

const int N=1e5+5; bool mark[N]; int prim[N],d[N],num[N]; int cnt; void getFactorNum() { cnt=0; d[1]=1; for (int i=2 ; i<N ; ++i) { if (!mark[i]) { prim[cnt++]=i; num[i]=1; d[i]=2; } for (int j=0 ; j<cnt && i*prim[j]<N ; ++j) { mark[i*prim[j]]=1; if (!(i%prim[j])) { num[i*prim[j]]=num[i]+1; d[i*prim[j]]=d[i]/(num[i]+1)*(num[i*prim[j]]+1); break; } d[i*prim[j]]=d[i]*d[prim[j]]; num[i*prim[j]]=1; } } }
<2>约数和

/* 约数和 sd[i] 表示 i 的约数和 sp[i] 表示 i 的最小素因子的等比数列的和 (我不知道怎么形容这个啊,就上面说要保存的那一项) prim[i] 表示第 i 个素数 */ const int N=1e5+5; 线性塞打表约数和 bool mark[N]; int prim[N]; long long sd[N],sp[N]; int cnt;//prim个数 void primeSum() { cnt=0; sd[1]=1; for (int i=2 ; i<N ; ++i) { if (!mark[i]) { prim[cnt++]=i; sd[i]=i+1; sp[i]=i+1; } for (int j=0 ; j<cnt && i*prim[j]<N ; ++j) { mark[i*prim[j]]=1; if (!(i%prim[j])) { sp[i*prim[j]]=sp[i]*prim[j]+1; sd[i*prim[j]]=sd[i]/sp[i]*sp[i*prim[j]]; break; } sd[i*prim[j]]=sd[i]*sd[prim[j]]; sp[i*prim[j]]=1+prim[j]; } } }
(6)模运算

运算规则: (a + b) % p = (a % p + b % p) % p (a - b) % p = (a % p - b % p) % p (a * b) % p = (a % p * b % p) % p (a ^ b) % p = ((a % p) ^ b ) % p 模运算的结合律: ((a + b) % p + c) % p= (a + (b + c) % p) % p ((a * b) % p * c) % p = (a * (b * c) % p ) % p 交换律: (a + b) % p = (b+a) % p (a * b) % p = (b * a) % p 分配率: ((a +b) % p * c) % p = ((a * c) % p + (b * c) % p) % p
(7)组合数
<1>Lucas

/* lucas定理(求较大组合数 ,在除数时采用逆元运算 公式:C(n, m) % p = C(n / p, m / p) * C(n%p, m%p) % p 对于C(n / p, m / p),如果n / p 还是很大,可以递归下去 */ ll fac[mod+105],inv[mod+105]; void getInv() { fac[0]=fac[1]=inv[1]=1; for(int i=2;i<mod;i++) { fac[i]=fac[i-1]*i%mod; inv[i]=(mod-mod/i)*inv[mod%i]%mod; } } ll comb(int n, int m, ll p){//C(n, m) % p 组合数公式 if (m < 0 || m > n) return 0; return fact(n, p) * inv(fact(m, p), p) % p * inv(fact(n-m, p), p) % p; } ll Lucas(ll n,ll m)//Lucas对组合数的处理(化简 { if(m>n)return 0; if(n<mod && m<mod)return C(n,m); return Lucas(n/mod,m/mod)*C(n%mod,m%mod)%mod; } ll fact(){ }
<1>*扩展Lucas
(8)逆元
<0>逆元取模运算规则
(a / b) % p = (a * inv(b) ) % p = (a % p * inv(b) % p) % p
<1>乘法逆元(打表)
1.乘法逆元定义:// a和p互质,a才有关于p的逆元 如果ax≡1 (mod p),且gcd(a,p)=1(a与p互质),则称a关于模p的乘法逆元为x。
打表:
//逆元打表:原理;inv(a) = (p - p / a) * inv(p % a) % p int inv[MAXL];//求1-MAXL关于MOD的逆元 int init(){ inv[1] = 1; for(int i = 2; i < MAXL; i ++){ inv[i] = (mod - mod / i) * 1ll * inv[mod % i] % mod; } }
<2>费马小定理
//费马小定理:快速幂模板的 特别参数 //假如a是一个整数,p是一个质数,那么 是p的倍数//(注意a,p条件) //A * (a^(p-1)-1) =n*p -> 如果a不为p的倍数 ->
LL Fermat(LL a, LL p){//费马求a关于b的逆元 return pow_mod(a, p-2, p); }
<3>扩展欧几里得求逆元
//扩展欧几里得:a*x + b*y = 1 当a,b互质时有解,x为a关于b的逆元 LL inv(LL t, LL p){//如果不存在,返回-1 LL d, x, y; ex_gcd(t, p, x, y, d); return d == 1 ? (x % p + p) % p : -1; }
(7)中国剩余定理(同余方程)
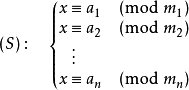

求解原理:通过转化为对应的逆元求解式求解 互质情况:假设整数m1,m2, ... ,mn两两互质,则对任意的整数:a1,a2, ... ,an, 方程组(S)有解 //n个方程:x=a[i](mod m[i]) (0<=i<n) LL china(int n, LL *a, LL *m){ LL M = 1, ret = 0; for(int i = 0; i < n; i ++) M *= m[i]; for(int i = 0; i < n; i ++){ LL w = M / m[i]; ret = (ret + w * inv(w, m[i]) * a[i]) % M; } return (ret + M) % M; } 对于不互质的情况: #include<cstdio> #include<algorithm> using namespace std; typedef long long LL; typedef pair<LL, LL> PLL; LL a[100000], b[100000], m[100000];//对应的线性方程输入数组 PLL linear(LL A[], LL B[], LL M[], int n) {//求解(A[i])x = B[i] (mod M[i]),总共n个线性方程组 LL x = 0, m = 1; for(int i = 0; i < n; i ++) { LL a = A[i] * m, b = B[i] - A[i]*x, d = gcd(M[i], a); if(b % d != 0) return PLL(0, -1);//答案不存在,返回-1 LL t = b/d * inv(a/d, M[i]/d)%(M[i]/d); x = x + m*t; m *= M[i]/d; } x = (x % m + m ) % m; return PLL(x, m);//返回的x就是答案,m是最后的lcm值 }
阶乘位数计算:

阶乘位数: 数据域:int 2^32 long long 64 #include<stdio.h> #include<math.h> void main() { int n,i; double d; scanf("%d",&n); d=0; for(i=1;i<=n;i++) d+=log10(i); printf("%d ",(int)d+1); } 32位以内:29!~30! 斯特林公式求阶乘位数(优化: #include<stdio.h> #include<math.h> #define PI 3.1415926 int main() { int cases,n,ans; scanf("%d",&cases); while(cases--) { scanf("%d",&n); if(n==1) printf("1 "); else { ans=ceil((n*log(n)-n+log(2*n*PI)/2)/log(10)); printf("%d ",ans); } } return 0; } 大数阶乘位数:使用 log10(n)分解 //floor返回不大于x的最大整数 #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> using namespace std; typedef long long ll; const int maxn=1e7+7; int main(){ int T; ll n; double ans; scanf("%d",&T); while(T--){ scanf("%I64d",&n); ans=1; for(int i=1; i<=n; i++){ ans+=log10(i); } printf("%I64d ",(ll)floor(ans)); } }
