目录
简介
原理
代码
简介
所谓可持久化线段树,就是将线段树的各个历史版本存储起来,以达到通过利用历史信息解决问题的目的。
原理
以权值线段树为例,
我们来看看权值线段树是如何实现可持久化的。
给出一个空的权值线段树,依次插入四个数:
1 3 4 2
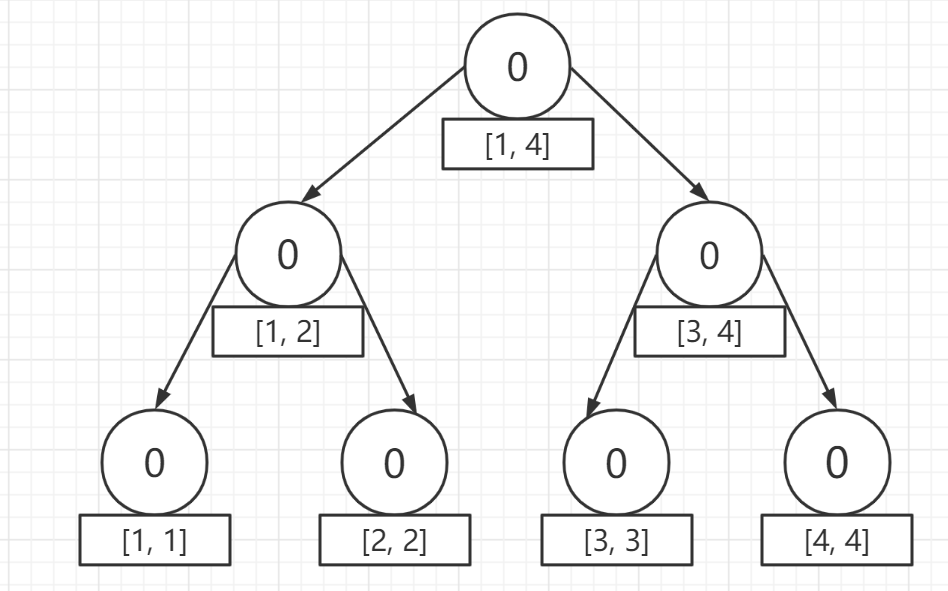
首先,这是空的树(记为第 (0) 个版本):(其中键值 (cnt) 表示区间元素个数)
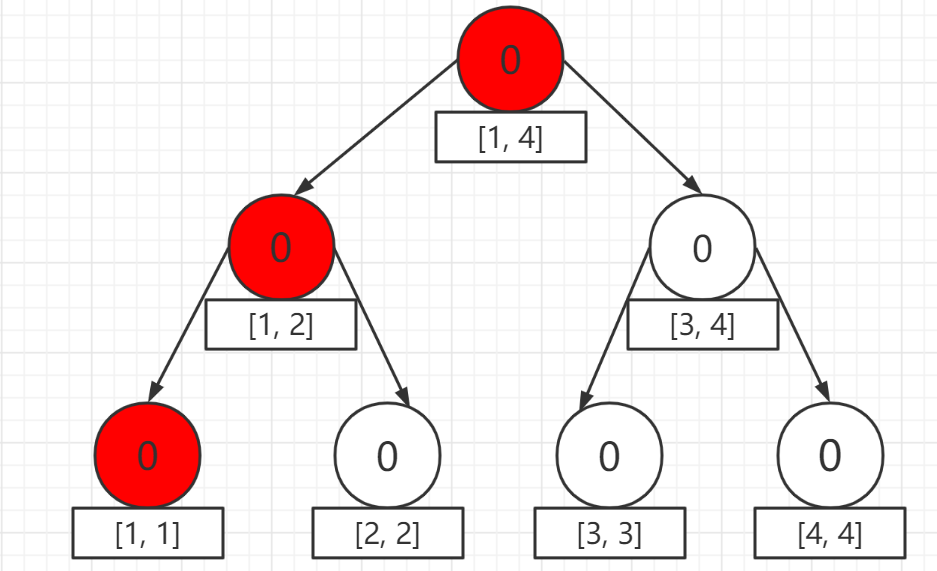
现在插入第一个元素 1 ,注意到我们要保留每一个历史版本,所以我们不是在原树上进行修改,但是我们不可能重新开一个新的线段树,那么开销太大,所以我们发生了修改的地方进行加点:
发生修改的地方:
加点:因为这个时候 1 的个数为 (1) ,而且其他结点的元素个数为 (0) ,所以相关的新增点键值 (cnt) 都是 (1) 。
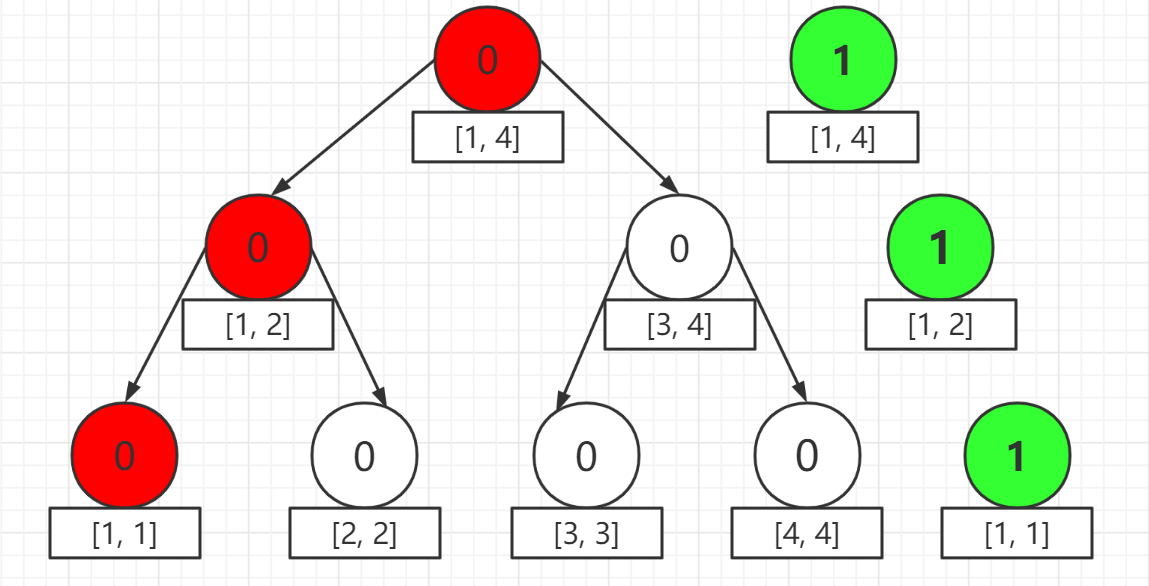
注意到这样一个事实:新点取代旧点后对应的线段树结构是完全不变的。
但是旧的节点并没有被删去。
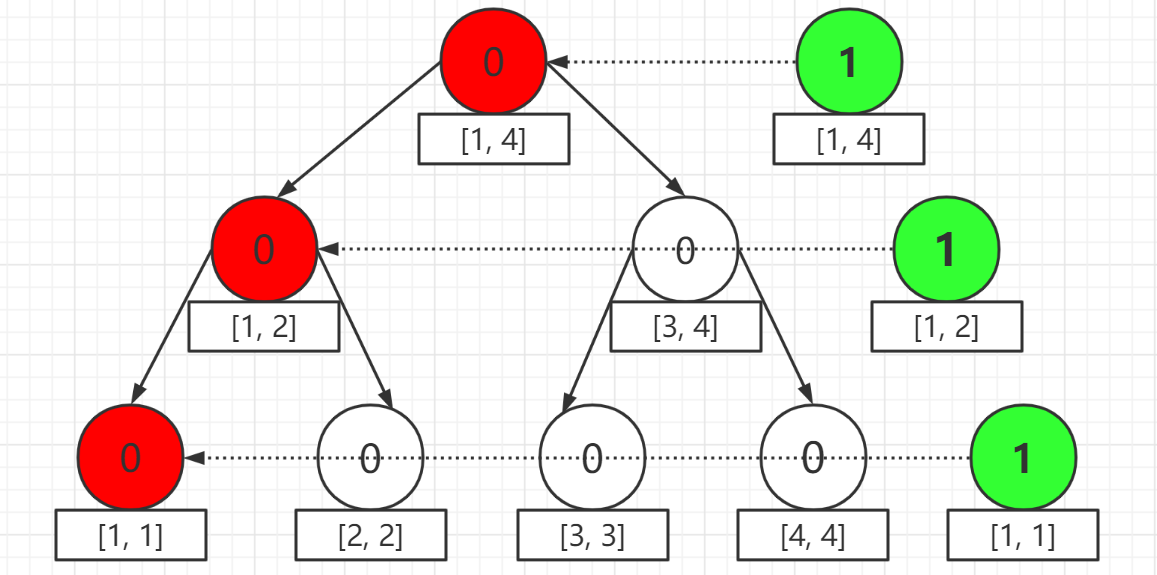
那么类似地,我们开始插入第二个元素 3,每次对于加点只需要基于上一个版本就可以了(红色结点表示发生修改的点),如图所示,(cnt) 也进行相应更新:
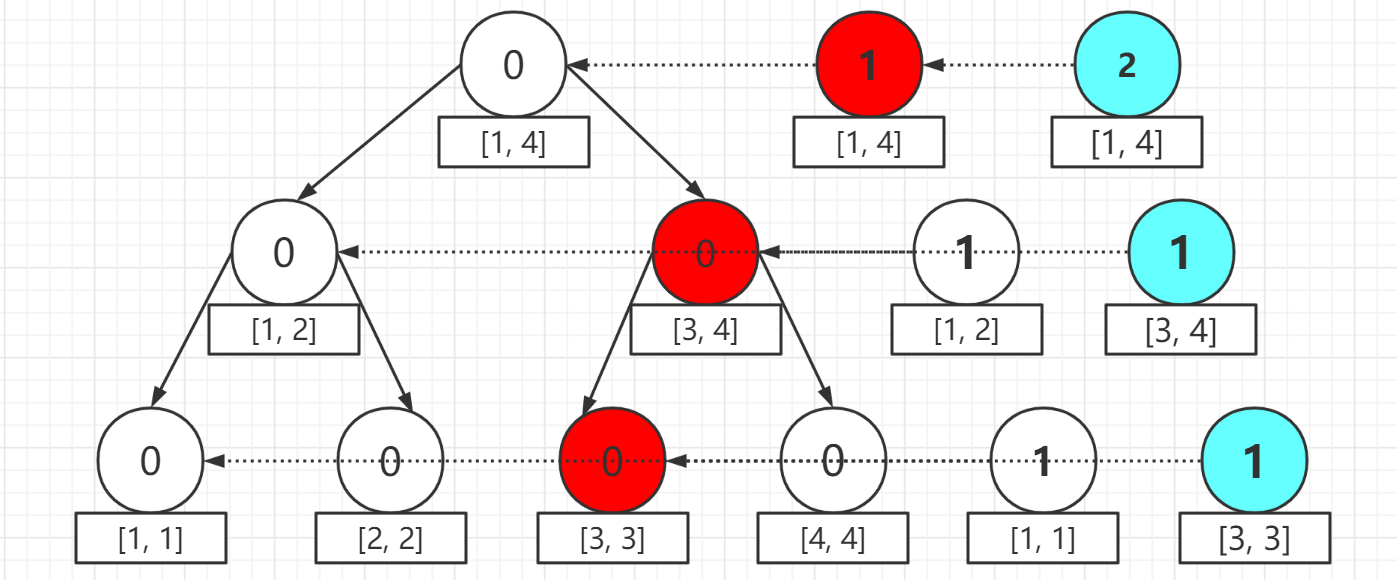
是不是有点晕,其实到目前,我们有三棵线段树:
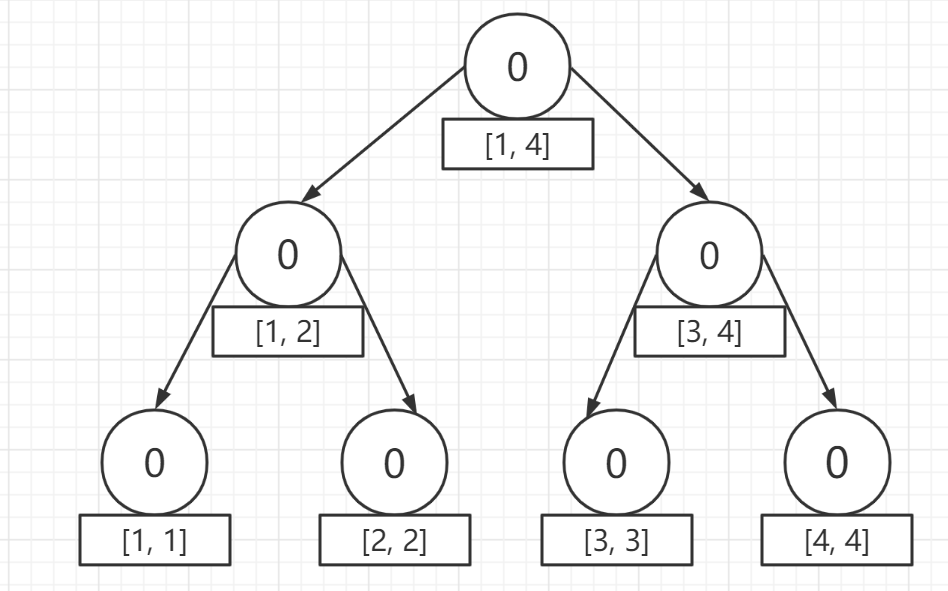
一开始的空树:
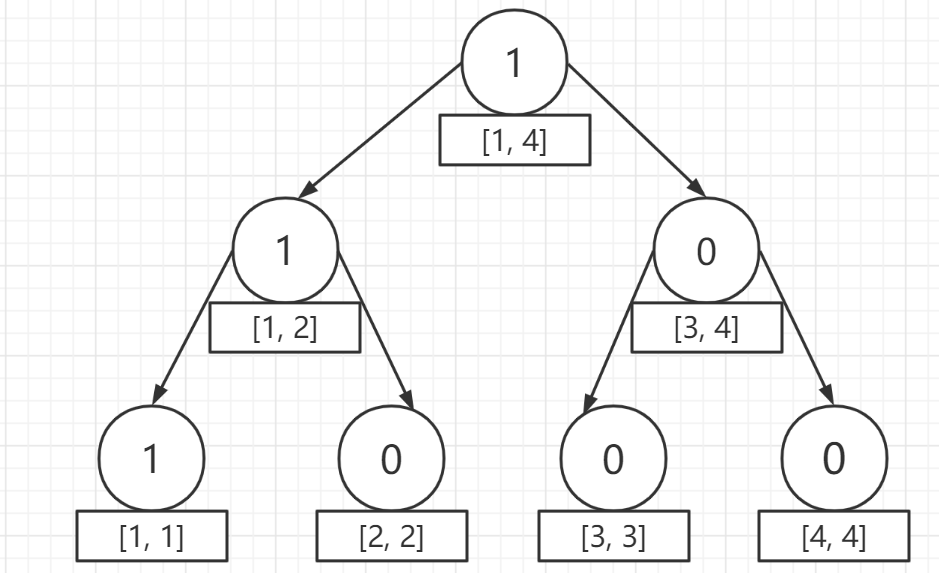
插入第一个元素后得到的第二棵树:
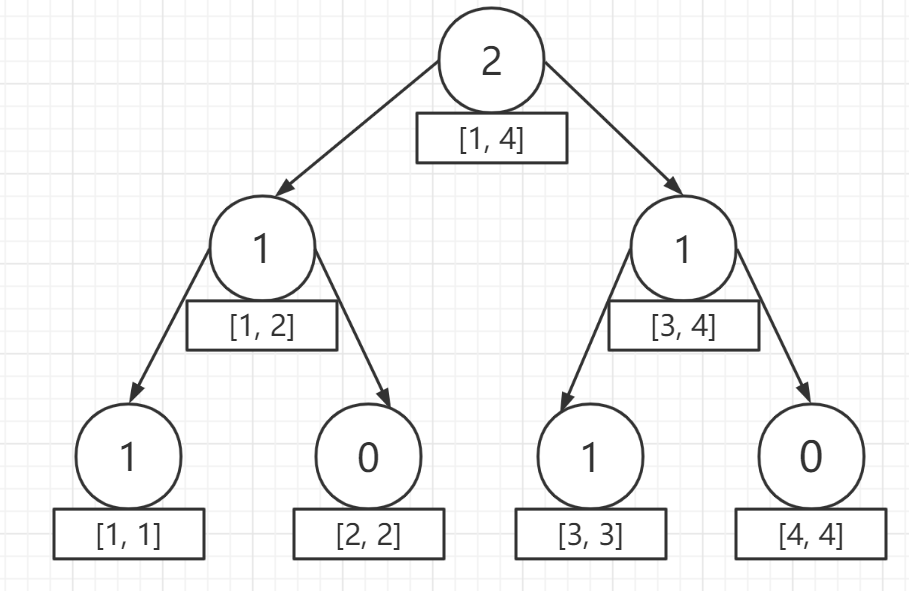
插入第二个元素后得到第三棵树:
而这三棵树,都储存在可持久化线段树的节点中。
第三第四个元素插入的操作类似于第二个元素插入操作:基于上一版本记录就好了。
模板题目传送门:https://www.acwing.com/problem/content/257/
结合模板题进行分析:
如果查询的区间是 ([1,n]) ,那么开一个权值线段树(不妨将它看成一个桶)就可以了,当查询的 $ k > cnt $ 时,我们向右子树递归,否则向左子树递归。
但是我们需要查询 ([l,r]) ,于是使用可持久化线段树来处理:查询 ([l,r]) 的 (k) 小数,基于前缀和的思想,无非是要知道第 (l-1) 到 (r) 次插入操作元素个数的情况,那么我们作个差就行了:将第 (r) 个版本对应节点的 (cnt) 减去 (l-1) 版本对应节点的 (cnt) 就能够获取相应地元素个数情况了,剩下的操作就是权值线段树的基本操作,结束。
代码
#include<bits/stdc++.h>
using namespace std;
/*
习惯约定:
u代表结点(编号)
p代表先前版本的位置指针
q代表最新版本的位置指针
*/
const int N=1e5+5, M=1e4+5;
int n,m;
int a[N];
vector<int> nums; // 离散化
int root[N];
int find(int x){
return lower_bound(nums.begin(),nums.end(),x)-nums.begin();
}
struct node{
int l,r; // 这里的 l,r 并非区间边界,而是指向左右儿子结点的编号的指针
int cnt; // 结点键值,维护个数。
}tr[4*N+17*N]; // 初始开的点数+logN * N (各版本总规模)
int idx;
// 返回建立的点的编号,两个参数分别代表左右边界。
int build(int l,int r){
int u=++idx;
if(l==r) return u;
int mid=l+r>>1;
tr[u].l=build(l,mid), tr[u].r=build(mid+1,r);
return u;
}
// 递归地插入
int insert(int p,int l,int r,int x){
int q=++idx;
tr[q]=tr[p];
if(l==r){
tr[q].cnt++;
return q;
}
int mid=l+r>>1;
if(x<=mid) tr[q].l=insert(tr[p].l,l,mid,x); // 如果更新的位置是在左边,那么 tr[q].l 为新开点
else tr[q].r=insert(tr[p].r,mid+1,r,x); // 否则 tr[q].r 为新开点
tr[q].cnt=tr[tr[q].l].cnt+tr[tr[q].r].cnt; // pushup the cnt
return q;
}
int query(int p,int q,int l,int r,int k){
if(l==r) return r;
int mid=l+r>>1;
int cnt=tr[tr[q].l].cnt-tr[tr[p].l].cnt;
if(cnt>=k) return query(tr[p].l,tr[q].l,l,mid,k);
else return query(tr[p].r,tr[q].r,mid+1,r,k-cnt);
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>a[i], nums.push_back(a[i]);
sort(nums.begin(),nums.end());
nums.erase(unique(nums.begin(),nums.end()),nums.end());
root[0]=build(0,nums.size()-1); // 第0个版本指的就是空的线段树。
for(int i=1;i<=n;i++)
root[i]=insert(root[i-1],0,nums.size()-1,find(a[i]));
while(m--){
int l,r,k; cin>>l>>r>>k;
cout<<nums[query(root[l-1],root[r],0,nums.size()-1,k)]<<endl; // 打印原来的值
}
return 0;
}