树状数组,顾名思义,是一个树形的数据结构,它的基本用途是较高效地维护序列的前缀和。
先补充几个知识:
-
lowbit运算:取出非负整数n在二进制下最低位的1以及它后边的0构成的数值。例如,若n=6,则n在二进制下表示为110,所以lowbit(n)=2。如何实现lowbit运算呢?设n>0,n的第k位是1,第0~k-1位都是0,则:
- 将n取反,此时第k位为0,第0~k-1位为1;
- 将n自加,即n=n+1,由于进位,此时第k位为1,第0~k-1位为0;
- 将前两步操作后的数与上n。
在前两步操作过后,n的第k+1位至最高位都与原来相反,所以三步操作后的数,即n&(~n+1),仅有第k位为1,其余位都为0。而在补码表示下,~n=-1-n,因此可以得出lowbit运算的公式:
lowbit(n)=n&(-n)
由于树状数组比较抽象,在讲解之前,先放一张概念图:
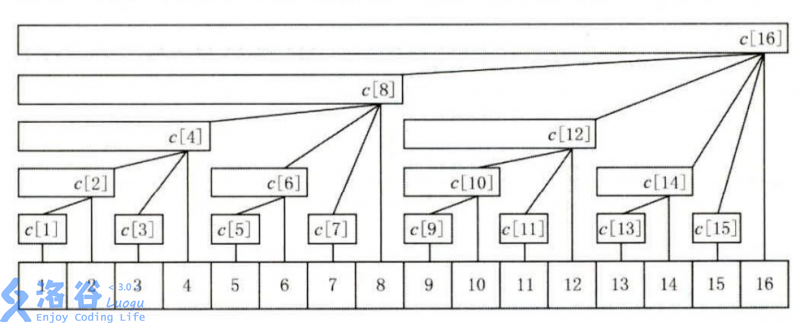
其中,c[x]存储区间[x-lowbit(x)+1,x]中所有数的和。
树状数组有以下几个性质:
- 每个内部节点c[x]存储以它为根的子树中所有叶节点的和
- 每个内部节点c[x]的子节点个数等于lowbit(x)的位数
- 除树根外,每个内部节点c[x]的父节点为c[x+lowbit(x)]
- 树的深度为O(logN)
正因为树状数组满足以上的性质,它才能高效地维护序列的前缀和。在实现过程中,我们只要建立一个树状数组c[N],按照以上的性质来进行对于树状数组的操作,就可以实现树状数组的功能。
与栈、队列等基础数据结构不同,进阶数据结构旨在高效地实现一些功能,可能会比较抽象,即使是树状数组、线段树这些比较简单的数据结构在刚开始接触的时候也会显得难以理解,不像初等数据结构那样直观。所以,读者在初步理解的基础上,应该多加练习,才能逐渐熟练地运用。
实际上,对于树状数组,读者不必纠结于其内部如何实现(虽然这也很好理解)以及为何这样实现等问题,主要还是应该理解应用的步骤。
本文将讲解树状数组的基本操作与简单的拓展操作,进阶操作请滑至本文末尾。
基本操作
树状数组支持的基本操作有两个,一是查询前缀和,二是单点修改。下面会一一进行讲解。
查询前缀和
前缀和虽然可以通过递推得出,但其时间复杂度为0(N),相对来说没有那么高效。而树状数组可以实现O(logN)地查询前缀和。
根据树状数组的定义,c[x]存储区间[x-lowbit(x)+1,x]中所有数的和,而我们要查询前缀和即为区间[1,x]中所有数的和。设要查询的前缀和为sum[x],则有:
sum[x]=...+c[x-lowbit(x)]+c[x]
这个很容易证明,因为c[x]存储区间[x-lowbit(x)+1,x]中所有数的和,c[x-lowbit(x)]存储区间[x-lowbit(x)-lowbit(x-lowbit(x))+1,x-lowbit(x)]中所有数的和,以此类推,直至左端点为1的区间,将其相加,就可以得出sum[x]了。
以查询sum[14]为例,一共会加上c[14],c[12],c[8],即分别为区间[13,14],[9,12],[1,8]中所有数的和,即为第14个元素的前缀和了。
代码实现:
int ask(int x)
{
int ans=0;
for( ;x;x-=x&-x)
ans+=c[x];
return ans;
}//查询第x个节点的前缀和
单点修改
单点修改,顾名思义就是对序列中的某一个元素进行数值修改。这个很容易实现,只要对所有的存储有该元素的节点进行修改即可。从该元素所在的叶子节点开始,不断地找到其父亲节点,直到树根,就可以高效地实现修改。如何找到父亲节点呢?利用前面提到的树状数组的第三条性质就可以了。时间复杂度0(logN)。
代码:
void add(int x,int d)
{
for( ;x<=N;x+=x&-x)
c[x]+=d;
}//对x元素加上d
拓展操作
除了两个基本操作外,树状数组通过一些巧妙的方法也可以实现一些拓展操作。下面讲解三个操作:单点查询,区间修改和区间查询。
单点修改与区间查询
这个很容易实现。对于单点修改基础上的区间查询,使用树状数组维护前缀和自然是很好的一个办法,只要在两个基本操作的基础上稍加修改即可实现。单点修改在这里就不再赘述了,而区间查询也极其简单。若需要查询区间[l,r]中所有数的和,只需要先查询元素r的前缀和,再查询元素l-1的前缀和,然后相减就可以得出答案。具体代码请读者自行实现。
单点修改与单点查询
单点修改基础上的单点查询就是左右端点相等的区间查询,在这里就不再赘述。
区间修改与单点查询
如果对区间内每个元素分别进行单点修改,显然时间复杂度过高。这里就需要一个差分的思想。若我们建立一个数组来存储每个元素修改的值,对于某一次操作对区间[l,r]中的每个数加上d,若将数组中所有相邻的两个数,后面的数减去前面的数,得出结果并存入数组,我们会发现,对于该操作,实际上只改动了两个元素的值,即第l个和第r+1个元素的值,分别为d和-d。这样我们就可以高效地实现区间修改了。而单点查询,只要计算出该元素修改过的值,加上初始值即可。如何计算呢?很简单,因为我们修改的值是进行差分过的,只要逆向处理,即求出对应元素的前缀和即可。
具体如何操作呢?建立一个树状数组来维护所有操作对于每一个元素修改的值,对于某一个区间修改操作对区间[l,r]中的每个数加上d,则将第l个元素加上d,第r+1个元素减去d。而对于某一个单点修改操作查询元素x的值,只要查询树状数组中x对于的前缀和,并加上x的初始值即可。
通过以上的巧妙的方法,就将区间修改与单点查询转换为单点修改和区间查询了。具体代码请读者自行实现,难度不大。
区间修改与区间查询
区间修改基础上的区间查询实际上是线段树所擅长的功能,但用树状数组也可以实现。
如果对区间内每个元素分别进行单点查询,显然时间复杂度过高。按照单点查询的思路,我们建立数组a存储原始序列,数组b存储每一个元素修改的值。前面有说过,对于元素x,b[x]的前缀和即为a[x]增加的值。而a[x]的前缀和增加了多少呢?显然就是区间[1,x]中每个元素在b数组中的前缀和相加,用公式表示即为:
(sum _{i=1}^{x} sum _{j=1}^{i}b[j])
但是我们可以发现,这个公式中包含有两个变量i和j,边界分别为x和i,对于每次查询,无法确定x和i的值,导致计算变得比较复杂。所以我们还需要将这个公式变换一下:
(sum _{i=1}^{x}sum _{j=1}^{i}b[j]= sum _{i=1}^{x}left ( x-i+1 ight )*b[i]= left ( x+1 ight )sum _{i=1}^{x}b[i]-sum _{i=1}^{x}i*b[i])
可以用图形来直观地解释以上的公式:
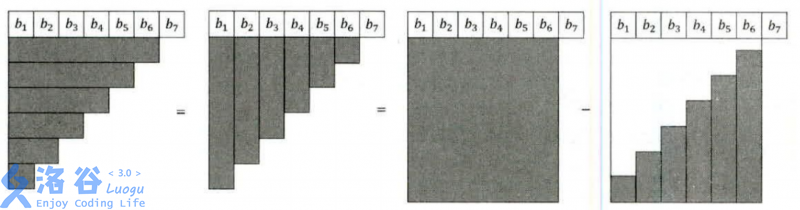
得出公式后,问题就变得简单很多了。公式中需要求两个前缀和,所以我们建立两个树状数组,一个维护b[i]的前缀和,另一个维护i*b[i]的前缀和即可。对于区间修改,用类似区间修改基础上的单点查询的方法,分别进行端点修改;对于区间查询,只要用上公式和查询前缀和的操作,查询出该区间修改的值,再加上该区间的原始值即可。
代码:
#include<iostream>
#define ll long long
using namespace std;
const int N=2e5;
ll n,m,cn,c[3][N];//c[0]维护b[i]的前缀和,c[1]维护i*b[i]的前缀和,c[2]维护原始序列的前缀和
void add(int k,int x,ll d)
{
for( ;x<=n;x+=x&-x)
c[k][x]+=d;
}
ll ask(int k,int x)
{
ll ans=0;
for( ;x;x-=x&-x)
ans+=c[k][x];
return ans;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>cn;
add(2,i,cn);
}
while(m--)
{
int x,a,b;
cin>>x>>a>>b;
if(x==1)
{
ll c;
cin>>c;
add(0,a,c);
add(0,b+1,-c);
add(1,a,a*c);
add(1,b+1,-(b+1)*c);
}
else
cout<<ask(2,b)+(b+1)*ask(0,b)-ask(1,b)-ask(2,a-1)-a*ask(0,a-1)+ask(1,a-1)<<endl;
}
return 0;
}
简单应用
利用基本操作,我们可以实现一些实际问题的应用。树状数组有一个非常经典的应用——求逆序对。
树状数组求逆序对
逆序对,即对于一个数列中的任意两个数,设其下标分别为 m_1,m_2m1,m2 ,大小分别为 n_1,n_2n1,n2 ,若 m_1<m_2m1<m2 且 n_1>n_2n1>n2 ,则称这两个数为一个逆序对。众所周知,逆序对可以用归并排序来求。树状数组也可以比较高效地求逆序对,并且实现简单,在实际中应用也不少。
我们通过证明很容易发现,只要遍历一个数列中的每一个数,找到在它后面且比它大的数的数量,并把这些数量相加,就是这个数列中逆序对的数量。所以,我们可以在这个数列的数值范围上建立一个树状数组,倒序输入这个数列,对于每一个数,查询它的数值的前缀和,之后将其的数值插入树状数组。把每个数的前缀和相加即为答案。
这个很容易证明:由于是倒序输入,所以在输入当前数之前,存储在树状数组中的都是在它后面的元素,而树状数组存储的是每个数值出现的个数,因此查询当前数的数值的前缀和,就相当于查询在当前数后面且比它小的数的数量。而将这些数量相加,自然就是这个数列的逆序对的个数了。
有一个需要注意的点:由于树状数组是建立在数列的数值范围上的,当数值范围较大时,要先对数列进行离散化。这里需要注意的是,在离散化的过程中,对于数值相等的元素,排在后面的元素映射得到的数值应该比排在前面的元素大,否则会将其误记为逆序对。
对于求逆序对的方法,应该按照题意来选择方法,有时候归并排序也会比树状数组更优,不过树状数组实现起来更为方便。具体代码请读者自行实现,难度不大。
当然,树状数组还有很多其它的应用,读者可以自行参考其它的进阶博客。
关于树状数组的进阶操作:
下面是两篇不错的树状数组进阶讲解,欢迎食用:
习题:
声明:本文中图片及部分文字引用于lyd的蓝书。
2019.4.26 于厦门外国语学校石狮分校