树状数组类似于线段树的变形。。
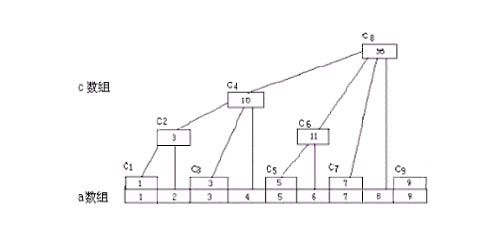
c[i]表示其子树的所有叶子节点的A[]之和
c[4]=A[1]+A[2]+A[3]+A[4]
c[6]=A[5]+A[6]
不难看出:c[i]代表的一定是一个连续的区间
对于lowbit[]数组:就是求得最后一个1 在倒数第几位,然后将其得出的结果加上x自身就可以得出当前节点的父亲节点的位置,或者是x减去其结果就可以得出上一个父亲节点的位置。
举个例子吧:比如当前是6,二进制就是0110,k为2,那么6+2=8,而C(8)则是C(6)的父亲节点的位置;
相反,6-2=4,则是C(6)的上一个父亲节点的位置。
容易发现,同一层中最低位1的位置相同
又发现,同一层中,每个节点的
区间长度也相同
**重点来了!!
只保留最低位1,换回十进制,就是区间长度**
同样找规律,发现:
节点编号+区间长度=父亲编号
那么问题来了:给出一个数,如何快速在二进制下只保留最低位1?
答案就是利用位运算,就不具体解释了,需要用到计算机储存原理——补码。。(我表示不会)
位运算:lowbit(x)=x&(-x);
注意:lowbit[]无法处理0的情况,因为它的结果也是0,那么最终就是一个死循环
_
接下来来看如何用树状数组进行单点修改和前缀和查询 _ __
(洛谷树状数组模板 1 )
前缀和查询:
比如我们要求sum[7], 7 = 111(2)
通过lowbit分解,可以变成 3 个数的和:111(2) = 1(2) + 10(2)+ 110(2)。其中 x (2) 表示x的二进制数。然后我们分析这个倒着跳的过程。7减去lowbit[7]得到6。6减去lowbit[6]得到4。4减去lowbit[4]得到0,就结束了;
主要代码就是这样咯,嘻嘻
int query(int u){
int ans = 0;
while(u >0){
ans += c[u];
u -= (u & -u);
}
return ans;
}
在这里我们拓展一下:
想一想我们怎么求任意区间的和呢??
答案其实不难哦,假如求得是[l , r]
那么ans = query(r) - query(l - 1)。
就这样 欧啦!
单点修改:
要将a[x] += w,就是要将c[]数组中有这个点的全部加上 w ,也就是说要在单点修改的同时,维护c[]数组

还是这个图,如果要把a[3] 加上w ,加的同时就需要维护包含a[3]的数组c[4]和c[8]。
清楚了吧,附上代码,完美。
void updata(int u,int w){
//在a[u]加上w
while(u <= n){
c[u] += w;
u += (u & -u);
}
}
告诉你个秘密:
树状数组有O(n)的初始化方法哦!(不要告诉别人)
void init(){
memset(c,0,sizeof();
for(int i=1;i<=n;i++){
c[i] += a[i];
if(i + (i & -i) <= n)
c[i + (i & -i)] += c[i];
}
}
嘘嘘
然后我们来看一下区间修改和单点查询
先补充一下关于差分的知识,对于a1,a2,a3,....,an这个序列,设一个数组b[i] = a[i] - a[i -1]
| 1 | 2 | 3 | 4 | 5 | 6 |7 |
:----------: | :----------: | :----------: | :----------: | :----------: | :----------: |
A| 2 | 3 | 1 | 2 | 5 | 7 | 4
B| 2 | 1 | -2 | 1 | 3 | 2 |-3
哎呀这个表格,费老劲了。。
**单点查询:
**
然后我们就发现b[1..i]的和 = a[i];
刚学的数列,我们用累加法来证明一下:
Sum{B[1..i]} = B[i]+B[i-1]+…+B[1]
=A[i]-A[i-1]+A[i-1]-A[i-2]+…+A[1]
=A[i]
**** 区间修改:****
考虑将区间[l , r]全部加上w,
那么对于l < i ≤ y,b[i]’ = (a[i] + w) - (a[i - 1] + w) = b[i]
对于i == l,b[l]’ = a[l] + w - a[l-1] = b[l] + w;
对于i == r + 1,b[r + 1]’ = a[r + 1] - (a[r] + w) = b[r + 1] - w
所以,区间修改对b[]的影响为:
b[l] += w,b[r + 1] -= w,b[l + 1..r]不变
单点查询:
也就是求b[]的前缀和。
这样一来,对a[]的操作就是:
1、使b[l] + w,b[r + 1] + (-w)
2、求B[1..l]的和
贴上份代码理解一下:
#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
int ch,x,y,z,last,n,m,c[1000000];
int lowbit(int x){
return (x & -x);
}
void update(int x,int y){
while (x<=n){
c[x] += y;
x += lowbit(x);
}
}
int query(int x){
int ans=0;
while (x>0){
ans += c[x];
x -= lowbit(x);
}
return ans;
}
int main(){
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++){
scanf("%d",&x);
update(i,x-last);
//这里运用了差分思想
//类似于a[i] - a[i-1]
last=x;
}
for (int i=1;i<=m;i++)
{
scanf("%d",&ch);
if (ch==1)
{
scanf("%d%d%d",&x,&y,&z);
update(x,z);
update(y+1,-z);
}
else
{
scanf("%d",&x);
printf("%d
",query(x));
}
}
}
自己打的代码中c[]实际就是储存的这个区间加了多少(比较于线段树add标记)
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
#define maxn 500001
using namespace std;
int n,m;
int p,x,y,k;
long long a[maxn],c[maxn];
//把x的二进制的高位1全部清空,只留下最低位的1
long long lowbit(int x)
{
return x & (-x);
}
//第x点增加v
void add(int x,int v)
{
while(x > 0)
{
c[x] += v;
x -= lowbit(x);
}
}
//求单点的和
long long sum(int x)
{
int ans=a[x];//c[i]不包括初始值 所以先加上
while(x <= n)
{
ans += c[x];
x += lowbit(x);
}
return ans;
}
/*
//任意区间和
int get_sum(int x1,int x2)
{
return sum(x2) - sum(x1);
}
*/
int main()
{
scanf("%d %d",&n,&m);
for(int i=1; i<=n; i++)
scanf("%lld",&a[i]);
for(int i=1; i<=m; i++)
{
scanf("%d",&p);
if(p==1)
{
scanf("%d %d %d",&x,&y,&k);
add(y,k);
add(x-1,-k);
//先把y之前的+k,再把x-1之前的-k 等价于 给[x,y]+k
}
if(p==2)
{
scanf("%d",&x);
printf("%lld
",sum(x));
}
}
return 0;
}
//一个数加一个负号是把这个数的二进制取反+1
//如-10的二进制就是-1010=0101+1=0110,然后用1010&0110,答案就是0010了
![lowbit[]数组](https://img-blog.csdn.net/20180906133225571?watermark/2/text/aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1ExNDEwMTM2MDQy/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70)