题面
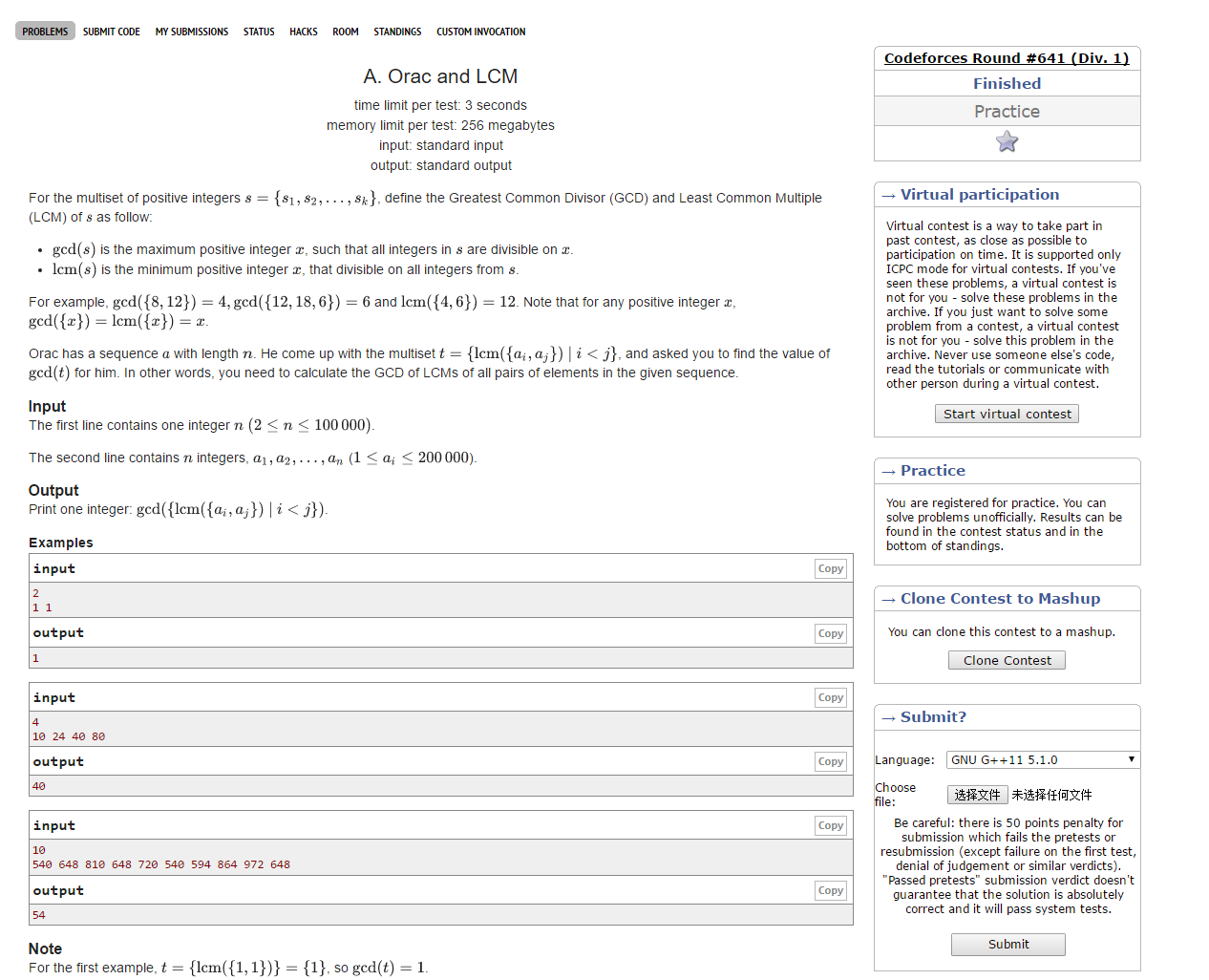
题目链接
https://codeforces.com/contest/1349/problem/A
题目大意
给你一个长度为 N 的数组,求 gcd {lcm({ai , aj}) | i < j}
解题思路
这道题有两种解法
① :
对于 a1 , 产生的 lcm 为 lcm(a1 , a2) , lcm(a1 , a3) ... lcm(a1 , an)
产生的 gcd_1 为 gcd ( lcm(a1 , a2) , lcm(a1 , a3) ... lcm(a1 , an) )
因为参与 gcd_1 的每一项都是 a1 的倍数
所以 gcd( lcm(a1 , a2) , lcm(a1 , a3) ... lcm(a1 , an) ) 可以化为 lcm (a1 , gcd (a2 , a3 , ... an) )
那么最后答案就为 ans = gcd( gcd_1 , gcd_2 , ... gcd_n ) , 我们维护一个后缀就可以搞定了
② :
假设 ai 没有 2 这个因子,且 aj 也没 2 这个因子,那么 lcm(a[i] , a[j]) 就不包含 2 这个因子
那么 ans = gcd {lcm({ai , aj}) | i < j} 也就不包含 2 这个因子
也就是说数组中如果有两个以上的数都不包含某个因子,那么答案也就不包含这个因子
所以我们可以对每个质因子开个容器,然后对每个数进行质因子分解
并将分解后质因子的幂次存于对应质因子的容器中
然后计算答案时判断每个质因子的容器大小是否大于等于 N - 1
如果是则说明数组中少于两个数没有这个质因子,则答案必定要乘上这个质因子
至于是该乘上这个质因子的几次方,我们对容器升序排个序
如果容器的大小等于 N 则取第二个元素即次小幂次,如果等于 N - 1则取第一个元素即最小幂次
以某质数容器的大小为 N 举例 :
最后一个元素对应最大幂次,只有一个数包含了这个它,倒数第二个元素对应次大幂次,有两个数包含了它
以此类推第二个元素对应次小幂次,有 N - 1 个数包含了它,第一个元素为最小次幂,有 N 个数包含了它
因为只需要 N - 1个数有包含它答案就可以乘上它,所以我们选第二个元素作为幂次
(这里次小不是严格意义上的次小,即 最小 <= 次小)
AC_Code ①
#include<bits/stdc++.h> #define int long long using namespace std; const int N = 3e5 + 10; int gcd(int a , int b) { return b ? gcd(b , a % b) : a; } int lcm(int a , int b) { return a * b / gcd(a , b); } int a[N] , suf[N]; signed main() { ios::sync_with_stdio(false); int n , ans = 0; cin >> n; for(int i = 1 ; i <= n ; i ++) cin >> a[i]; for(int i = n ; i >= 1 ; i --) suf[i] = gcd(suf[i + 1] , a[i]); for(int i = 1 ; i <= n ; i ++) ans = gcd(ans , lcm(a[i] , suf[i + 1])); cout << ans << ' ' ; return 0; }
AC_Code ②
#include<bits/stdc++.h> #define int long long using namespace std; const int N = 2e5 + 10; int prime[N] , minprime[N]; vector<int>vec[N]; int pow_mod(int x , int n) { int res = 1; while(n) { if(n & 1) res = res * x; x = x * x; n >>= 1; } return res; } int euler(int n) { int c = 0 , i , j; for(int i = 2 ; i <= n ; i ++ ) { if(!minprime[i]) prime[++ c] = i , minprime[i] = i; for(j = 1 ; j <= c && i * prime[j] <= n ; j++) { minprime[i * prime[j]] = prime[j]; if(i % prime[j] == 0) break; } } return c; } void get_prime(int n) { for(int i = 1 ; i <= n ; i ++) { int x = prime[i]; if(x * x > n) break ; if(n % x == 0) { int c = 0; while(n % x == 0) n /= x , c ++ ; vec[x].push_back(c); } } if(n > 1) vec[n].push_back(1); } signed main() { ios::sync_with_stdio(false); int cnt = euler(N - 10); int n , x , ans = 1; cin >> n; for(int i = 1 ; i <= n ; i ++) { cin >> x; get_prime(x); } for(int i = 1 ; i <= cnt ; i ++) { int x = prime[i]; sort(vec[x].begin() , vec[x].end()); if(vec[x].size() == n) ans *= pow_mod(x , vec[x][1]); else if(vec[x].size() == n - 1) ans *= pow_mod(x , vec[x][0]); } cout << ans << ' ' ; return 0; }