给定一个数组a[n],求数组a[n]的和sum。一般的方法是遍历数组然后求和,这样的时间复杂度为O(n)。而当修改了数组中的元素,再次求数组的和时,又要付出O(n)的时间代价。此时,我们可以用树状数组来求和数组的和。得到树状数组C[n]后,时间复杂度将由O(n)变为O(lgn)。这是如何实现的呢?下面我们将按照:
Lowbit()函数-->树状数组-->树状数组索引的意义-->树状数组的求和函数-->被操作数组更新数据,顺序介绍这一巧妙的神器。
(1)lowbit()函数
Lowbit()函数是对整数的位操作,返回一个二进制数的最低位“1”。如10(10)=01010(2),返回最低位的“1”,即2。lowbit()函数不是库函数,需要自己定义。
int lowbit(int x)
{
return x&-x;
}
原理(以10为例):
运用计算机的补码运算规则:原码取反+1。
原码取反后,各位与原二进制数相反,lowbit位(含)以后全变为1:
原码:01010
反码:00101
反码加一后,二进制的属性导致各位都受影响(从最低位向高位进一,直到遇到一个0位变为1):
补码:00110
此时,lowbit位前各位与原码相反,lowbit位相等,lowbit位后全为0。
将补码与原码进行&(与)运算,便可得到只有lowbit位为1的二进制数。
原码:01100
补码:00110
结果:00100(与运算后)
int lowbit(int x)
{
return x&(x&(x^(x-1));
}
亦可实现返回最低位“1”,读者可自行推导。
(2)树状数组
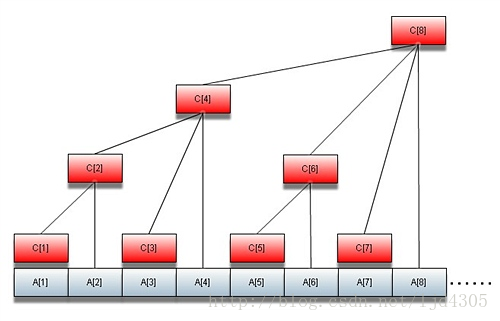
如图所示为树状数组的表示形式,下面给出树状数组的定义: Cn=a(n-a^k+1)+......+a(n)(k为n的二进制表示中从右向左数的0的个数,a^k可用lowbit函数求出)。到此,读者也许在思考此图划分的原因吧。这正是本人思考了很久的点,下面通过数组索引(下标)的意义来理解这种结构。
(3)树状数组索引的意义
在图中我们可以看到树状数组c的索引与要求和的数组a的索引是一一对应的。暂且理解数组c的下标意义为对数组a求和的元素数量。
c[1]=a1(a数组第1个数,下同) 1:0001
c[2]=a1+a2 2:0010
c[3]=a1+a2+a3 3:0011
c[4]=a1+a2+a3+a4 4:0100
c[5]=a1+a2+a3+a4+a5 5:0101
c[6]=a1+a2+a3+a4+a5+a6 6:0110
c[7]=a1+a2+a3+a4+a5+a6+a7 7:0111
c[8]=a1+a2+a3+a4+a5+a6+a7+a8 8:1000
可见每一位索引对应的处理元素个数都可通过索引二进制表示后不断进行lowbit操作求得:7=0001+0010+0100=1+2+4。而lowbit位以前的非零位则是已经处理过的。为了实现与lowbit前非零位的衔接((2)中的Cn公式),索引对应的元素在被操作数组a中的操数量即为索引的lowbit。即当前处理位置减去已经处理过的元素数量。之前的计算结果可通过不断进行n-=lowbit(n)得到(n为当前索引值)。
在此以c[7]和c[8]为例(此例中索引为在数组的位序,即下标从1开始):
c[7]=a[7-lowbit[7]+1]+....+a[7].此处两索引相等,为a[7].
7-lowbit(7)=6
C[6]=a[6-lowbit(6)+1]+....+a[6]=a[5]+a[6]
6-lowbit(6)=4
C[4]=a[4-lowbit(4)+1]+.....+a[4]=a[1]+a[2]+a[3]+a[4]
4-lowbit(4)=0,结束。
c[8]=a[8-lowbit(8)+1]+...+a[8]=a[1]+a[2]+...a[8]
8-lowbit(8)=0,结束。
由此可以结合树状数组下标的意义理解上图的结构。
(4)求数组的和:
int Sum(int n)
{
int sum=0;
while(n>0)
{
sum+=c[n];
n-=lowbit(n);/*此处便可看出时间复杂度O(lgn)的由来。因为每次lowbit运算都是对原操作数除以二。*/
}
return sum;
}
(5)被操作数组更新数据(对a中第i个数加x)
此时可以更好的体现树状数组的优势:O(lgn)
void change(int i,int x)
{
while(i<=n)
{
c[i]=c[i]+x;
i+=lowbit(i);
}
}
未得到博主允许转载者,不追究任何责任,欢迎大家给出更好的理解方式。