以实数 -9.625 为例,来看看如何将其表达为单精度的浮点数格式。具体转换步骤如下:
1、首先,需要将 -9.625 用二进制浮点数表达出来,然后变换为相应的浮点数格式。即 -9.625 的二进制为 1001.101,用规范的浮点数表达应为 1.001101×23。幂次等于小数点移动的位数
2、其次,因为 -9.625 是负数,所以符号段为 1。而这里的指数为 3,所以指数段为 3+127=130,即二进制的 10000010。有效数字省略掉小数点左侧的 1 之后为 001101,然后在右侧用零补齐。因此所得的最终结果为:
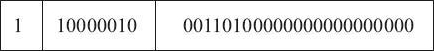
3、最后,我们还可以将浮点数形式表示为十六进制的数据,如下所示:
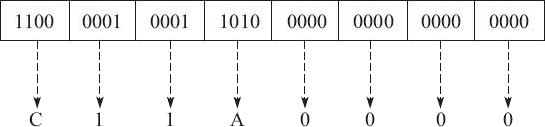
即最终的十六进制结果为 0xC11A0000。
我们知道,指数可以为正数,也可以为负数。为了处理负指数的情况,实际的指数值按要求需要加上一个偏置(Bias)值作为保存在指数段中的值。因此,这种情况下的指数段被解释为以偏置形式表示的有符号整数。即指数的值为:E=e-Bias
其中,e 是无符号数,其位表示为 ek-1…e1e0,而 Bias 是一个等于 2k-1-1(单精度是 127,双精度是 1023)的偏置值。由此产生指数的取值范围是:单精度为 -126~+127,双精度为 -1022~+1023。
对小数段 frac,可解释为描述小数值 f,其中 0≤f<1,其二进制表示为 0.fn-1…f1f0,也就是二进制小数点在最高有效位的左边。有效数字定义为 M=1+f。有时候,这种方式也叫作隐含的以 1 开头的表示法,因为我们可以把 M 看成一个二进制表达式为 1.fn-1fn-2…f0 的数字。既然我们总是能够调整指数 E,使得有效数字 M 的范围为 1≤M<2(假设没有溢出),那么这种表示方法是一种轻松获得一个额外精度位的技巧。同时,由于第一位总是等于 1,因此我们就不需要显式地表示它。拿单精度数为例,按照上面所介绍的知识,实际上可以用 23 位长的有效数字来表达 24 位的有效数字。比如,对单精度数而言,二进制的 1001.101(即十进制的 9.625)可以表达为 1.001101×23,所以实际保存在有效数字位中的值为:
00110100000000000000000
即去掉小数点左侧的 1,并用 0 在右侧补齐。