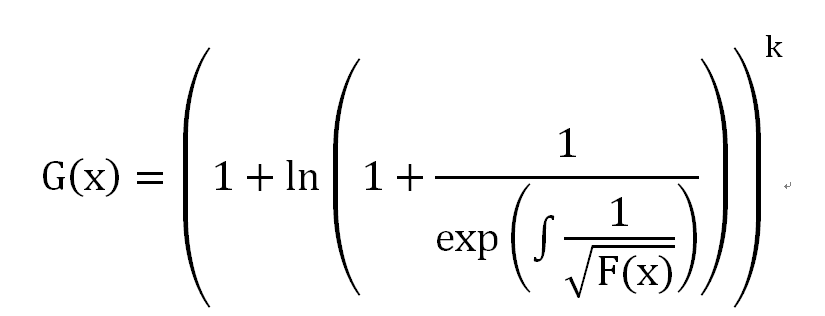原创by Sky_miner
定义部分纯属口胡,有不严谨的地方可以在下面评论。
所有代码在最后给出
前置技能
多项式的表示
系数表示法
定义一个多项式(f(x) = sum_{i=0}^na_ix^i)前式之中(x)是一个不定元,不表示任何值
则我们可以使用({a_1,a_2,...,a_{n-1},a_n})来表示一个多项式的系数。
其中(n)即最高次项的次数则被称作多项式(f(x))的度数或次数,一般记作(deg_f)
点值表示法
定义一个多项式(f(x)),并用多个点对((x_i,y_i))表示,满足对任意的(i ext{都有} f(x_i) = y_i),且这个多项式可以由这些点对唯一确定.
一般点值表示法只用于加速多项式乘法,也就是我们常说的快速傅立叶变换(Fast Fourier Transform, FFT)
复数
复数分为实部和虚部,形式为(a + bi)其中(i^2 = -1).
复数运算
加法((a_1+a_2) + (b_1+b_2)i)
减法((a_1-a_2) - (b_1-b_2)i)
乘法((a_1+b_1i)*(a_2+b_2i) = (a_1*a_2 - b_1*b_2) + (a_1*b_2 + a_2*b_1)i)
对实数的运算则使实部和虚部同时对那个数进行运算
单位根
(n)次单位根为满足(z^n = 1)的复数,这样的复数共有(n)个且均匀分布在复平面的一个单位圆上。
由数学知识可得,(n)次单位根为
且(e^{θi} = cos θ + isin θ)
我们记(omega_n = e^{frac{2πi}{n}}),则(n)次单位根为(omega_n^0,omega_n^1,...,omega_n^{n-1})
多项式的求导及积分
求导和积分互为逆运算
求导有:(g_i = f_{i+1}*(i+1))且(g_n = 0)
积分有:(g_i = f_{i-1}/i)且(g_0 = 0)
复杂度均为(O(n))
正片开始:多项式的运算
计算多项式的和即(A(x) + B(x))
即给定多项式(A(x),B(x))
求一个多项式(C(x))满足
系数对位相加,复杂度(O(n));
计算多项式的差即(A(x) - B(x))
即给定多项式(A(x),B(x))
求一个多项式(C(x))满足
系数对位相减,复杂度(O(n));
计算多项式的乘积即(A(x) * B(x))
即给定多项式(A(x),B(x))
求一个多项式(C(x))满足(C(x) = sum_{i=0}^{2n}c_ix^i)
我们可以直接暴力计算,复杂度(O(n^2))
我们之前说过点值表示法主要用于快速计算卷积.卷积通俗地来理解其实就是求所有满足(i+j)为一定值的一种计算形势。
所以这里要计算的其实就是一个卷积。
假设说我们多项式是采用的点值表示法,那么我们可以直接把两组点对((x_i,y_i))中所有的点对直接对位相乘,即得到了((x_i,y_{1_i}*y_{2_i}))
这样我们就得到了结果多项式的点值表达方式,如果一直采用点值表达的话可以简化乘法运算,但是不利于观察多项式。(毕竟你不能直接看着一堆二元对当多项式用)
所以我们需要一种快速将多项式表示形式转化的一种算法。FFT就是用来处理这个问题的,可以做到在(O(nlogn))内转化完成。所以就可以将乘法的复杂度降低到(O(nlogn))
Cooley-Tukey
该算法的证明及实现网上提到的很多,故不再说明。
(我才不告诉你我不会证明呢)
求多项式的逆元
求多项式(A(x))在((mod ext{ } x^n))意义下的逆元
即对于一个给定的多项式(f(x)),求一个多项式(B(x))
满足(A(x)B(x) equiv 1 (mod ext{ } x^n))
我们仍然采用分治的思想.
假设我们已知一个多项式(B^{'}(x))满足$$A(x)B^{'}(x) equiv 1(mod ext{ } x^{frac{n}{2}})$$
且我们当前求的多项式(B(x))一定满足$$A(x)B^(x) equiv 1(mod ext{ } x^{frac{n}{2}})$$
我们将上述两式作差,消掉(A(x))再平方,再乘上(A(x)),可以得到
因为(A(x)B(x) equiv 1 (mod ext{ } x^n))
所以最终化简得到$$B(x) = 2B^{'}(x) - A(x)B{'^2}(x)$$
注:不要忘记在得到的多项式中将所有次数>=mod的次数的项置零.
复杂度(O(nlogn))
多项式的除法和取余
问题即为:给定一个(n)次多项式(A(x))和一个(m)次多项式(B(x)),求出两个多项式(f(x),g(x))满足
且满足(deg_f leq n - m,deg_g < m)
我们发现,如果我们能消去(g(x)),就可以人为地规定一个mod,做逆元即可。
所以我们考虑如何消去(g(x))一项.
我们首先定义(f^R(x) = x^nf(frac{1}{x}))
其中(f^R(x))即为(f(x))的系数反转后得到的新的多项式。
(不理解可以自己写几个多项式试一试)
那么我们回到原式的(A(x) = f(x)B(x) + g(x))
我们首先可以不失一般性地设(deg_f = n-m,deg_g = m-1)不足则补零.
然后可以做如下变换:
然后我们把这个式子放在(mod ext{ } x^{n-m+1})的剩余系下,可以证明只有最后一项会被模去。
于是我们得到了这么一个式子(A^R(x) equiv f^R(x)B^R(x) (mod ext{ } x^{n-m+1}))
所以我们用刚刚提到的方法求出(B(x))的逆元即可计算出(f(x))
然后(g(x))的计算就不用多说了吧,(f(x))都有了...
复杂度(O(nlogn))
多项式的多点求值
问题即为:给出一个多项式(A(x))和(n)个点(x_0,x_1,...,x_{n-1})求(A(x_0),A(x_1),...,A(s_{n-1}))
实际上就是多项式向系数表达项点值表达上更一般的转化。由于不具有单位根的特殊性,故不能使用FFT.
但是我们依然可以从Cooley-Tukey的分治策略的角度上想:
我们考虑把求值序列和系数都分半,本别记分开的左右序列为(X,Y)
即:
我们设用(X)插值得到的序列为(f(x)),用(y)插值得到的序列为(g(x))
那么我们考虑将其合并为一个新的多项式.
首先我们构造这样的两个多项式
注:因下面的两部分完全相同,故只说明(F(x))的部分
这样,(F(x))的值为零当且仅当(x in X)
那么我们可以有(A(x) = C(x)F(x) + f(x))
这样的话在(x in X)时(C(x)F(x))一定为零,因此可以让(f(x))直接对(A(x))做出贡献
所以此时有(A(x) equiv f(x) (mod ext{ } F(x)))
多项式取余即可.
这样完成了子问题的合并,复杂度(O(nlog^2n))
多项式的快速插值
问题即为:给出(n+1)个二元数对((x_i,y_i)),要求求出一个(n)次多项式使所有的二元数对都在这个多项式上。
实际上就是多项式的点值表达向系数表达上更一般的转化。由于不具有单位根的特殊性,故不能使用FFT.
但是我们依然可以从Cooley-Tukey的分治策略的角度上想:
我们考虑把求值序列分半,本别记分开的左右序列为(X,Y)
即:
我们设用(X)插值得到的多项式为(f(x)),用(y)插值得到的序列为(g(x)),考虑构造(A(x))
依然设$$F(x) = prod_{i=0}^{frac{n}{2}}(x - x_i)$$
则(A(x) = g(x)F(x) + f(x))
那么现在问题就变为了将所有在(Y)中的点插值,使得
化简得
所以我们完成了子问题的递归。
复杂度(O(nlog^3n))
多项式求(ln)
问题即为:给定多项式(f(x))求一个多项式(g(x))满足(g(x) = ln ext{ }f(x))
我们将两边都求导可得
所以可以在(O(nlogn))内完成
多项式求(exp)
问题即为:给定一个多项式(f(x)),求一个多项式(g(x))满足(g(x) = e^f(x))
我们采用分治策略.
(这个公式我不会证)
设(g_0(x))为子问题((1~frac{n}{2}))中得到的结果
则我们有(g(x) = g_0(x)*(1 - lng_0(x) + f(x)))
迭代可以在(O(nlog^2n))内完成
多项式开根号
问题即为:给定一个多项式(f(x))求出一个多项式(g(x))满足g^2(x) = f(x)
我们设(g_0^2(x) equiv f(x)(mod ext{ } x^{frac{n}{2}}))
呢么我们有
那么我们就发现:
利用分治算法,我们可以在(O(nlogn))内完成
但是常数巨大,我们可以把常数也算成一个(log),也就是(O(nlog^2n))
多项式快速幂
问题即为:给定一个多项式(f(x))和一个整数(k)求一个多项式(g(x))满足(g(x) equiv f^k(x) (mod ext{ } x^n))
正常选手: 我们可以多次FFT每次除去所有次数>=n的项。
脑洞选手: 我们可以输出(exp(k ext{ }ln ext{ }f(x)))
Code:
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
template<typename T>inline void read(T &x){
x=0;char ch;bool flag = false;
while(ch=getchar(),ch<'!');if(ch == '-') ch=getchar(),flag = true;
while(x=10*x+ch-'0',ch=getchar(),ch>'!');if(flag) x=-x;
}
const int pri_rt = 3;
const int maxn=600010;
const int mod=998244353;
const int inv_2 = 499122177;
int n,k,N,C,len;
int rev[maxn],w[maxn];
int f[maxn];
int Inv[maxn],Ln[maxn],Exp[maxn],Sqrt[maxn];
inline int qpow(int x,int p){
int ret = 1;
for(;p;x=1LL*x*x%mod,p>>=1) if(p&1) ret=1LL*ret*x%mod;
return ret;
}
inline int check(int &x){
if(x < 0) x += mod;
if(x >= mod) x -= mod;
}
void FNT(int n,int *x,int flag){
for(int i=0,t=0;i<n;++i){
if(i > t) swap(x[i],x[t]);
for(int j=n>>1;(t^=j) < j;j>>=1);
}
for(int m=2;m<=n;m<<=1){
int k = m>>1;
int wn = qpow(pri_rt,flag == 1 ? (mod - 1)/m : (mod-1) - (mod-1)/m);
w[0] = 1;
for(int i=1;i<k;++i) w[i] = 1LL*w[i-1]*wn % mod;
for(int i=0;i<n;i+=m){
for(int j=0;j<k;++j){
int u = 1LL*x[i+j+k]*w[j] % mod;
x[i+j+k] = x[i+j] - u;check(x[i+j+k]);
x[i+j] = x[i+j] + u;check(x[i+j]);
}
}
}
if(flag == -1){
int inv = qpow(n,mod-2);
for(int i=0;i<n;++i) x[i] = 1LL*x[i]*inv%mod;
}
}
inline void get_dao(int n,int *f){
for(int i=0;i<n;++i) f[i] = 1LL*f[i+1]*(i+1) % mod;
f[n] = 0;
}
inline void get_fen(int n,int *f){
for(int i=n-1;i>=0;--i) f[i] = 1LL*f[i-1]*qpow(i,mod-2) % mod;
f[0] = 0;
}
void get_inv(int n,int *f){
static int g[maxn];
if(n == 1){
Inv[0] = qpow(f[0],mod-2);
return;
}
get_inv((n+1)>>1,f);
int len = n<<1;
for(int i=0;i<n;++i) g[i] = f[i];
fill(g+n,g+len,0);
FNT(len,g,1);FNT(len,Inv,1);
for(int i=0;i<len;++i){
Inv[i] = 1LL*Inv[i]*(2LL - 1LL*g[i]*Inv[i]%mod + mod) % mod;
}FNT(len,Inv,-1);fill(Inv+n,Inv+len,0);
}
void get_ln(int n,int *f){
int len = n<<1;
fill(Inv,Inv+(len<<1),0);
get_inv(n,f);get_dao(n,f);
FNT(len,f,1);FNT(len,Inv,1);
for(int i=0;i<len;++i) Ln[i] = 1LL*f[i]*Inv[i] % mod;
FNT(len,Ln,-1);fill(Ln+n,Ln+len,0);
get_fen(n,Ln);
}
void get_exp(int n,int *f){
static int g[maxn];
if(n == 1){
Exp[0] = 1;
return;
}
get_exp(n>>1,f);
int len = n<<1;
for(int i=0;i<n;++i) g[i] = Exp[i];
fill(g+n,g+len,0);
get_ln(n,g);
for(int i=0;i<n;++i) Ln[i] = ((i == 0) - Ln[i] + f[i] + mod) % mod;
FNT(len,Ln,1);FNT(len,Exp,1);
for(int i=0;i<len;++i) Exp[i] = 1LL*Exp[i]*Ln[i] % mod;
FNT(len,Exp,-1);fill(Exp+n,Exp+len,0);
}
void get_sqrt(int n,int *f){
static int g[maxn];
if(n == 1){
Sqrt[0] = sqrt(f[0]);
return;
}
get_sqrt(n>>1,f);
int len = n<<1;
fill(Inv,Inv+(len<<1),0);get_inv(n,Sqrt);
for(int i=0;i<n;++i) g[i] = f[i];
fill(g+n,g+len,0);
FNT(len,g,1);FNT(len,Inv,1);
for(int i=0;i<len;++i) g[i] = 1LL*g[i]*Inv[i] % mod;
FNT(len,g,-1);
for(int i=0;i<n;++i) Sqrt[i] = 1LL*(Sqrt[i] + g[i])*inv_2%mod;
}
void get_pow(int len,int *f,int p){
get_ln(len,f);
for(int i=0;i<len;++i) f[i] = 1LL*p*Ln[i]%mod;
fill(Exp,Exp+(len<<1),0);
get_exp(len,f);
}
int main(){
int n,k;read(n);read(k);
for(int i=0;i<n;++i) read(f[i]);
for(len=1;len<=n;len<<=1);
get_sqrt(len,f);
fill(Inv,Inv+(len<<1),0);get_inv(len,Sqrt);
for(int i=0;i<len;++i) f[i] = Inv[i];
get_fen(len,f);fill(f+n,f+len,0);
get_exp(len,f);
for(int i=0;i<len;++i) f[i] = Exp[i];
fill(Inv,Inv+(len<<1),0);get_inv(len,f);
for(int i=0;i<len;++i) f[i] = Inv[i];
++f[0];
get_ln(len,f);
for(int i=0;i<len;++i) f[i] = Ln[i];
++f[0];
fill(f+len+1,f+(len<<1),0);
get_pow(len,f,k);
for(int i=1;i<n;++i) printf("%d ",1LL*Exp[i]*i % mod);
puts("0");
getchar();getchar();
return 0;
}
该代码用于计算这样的一个式子