题目大意:
给出n个数(q_i)定义
[f_i = sum_{i<j}{frac{q_iq_j}{(i-j)^2}} - sum_{i>j}frac{q_iq_j}{(i-j)^2}
]
设(E_i = frac{f_i}{q_i}),求所有的(E_i)
题解:
我们把(f_i)代入(E_i)的表达式中,有
[E_i = sum_{i<j}{frac{q_j}{(i-j)^2}} - sum_{i>j}frac{q_j}{(i-j)^2}
]
然后我们考虑每个(q_i)对(E_i)的贡献
我们把贡献做成如下表格,每个格子上的值和列坐标的积是对行坐标的贡献
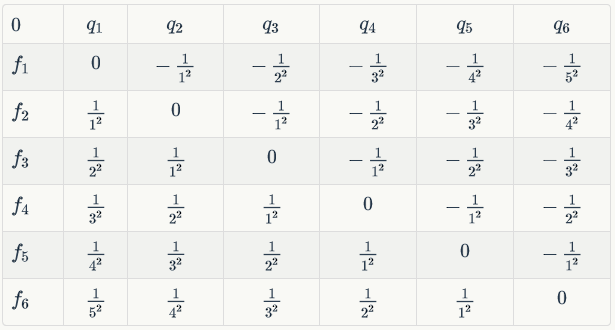
博客园吞我表格,,只能传图了
我们发现正负分布有规律,所以我们把正贡献的负贡献分开计算
我们发现它的每一部分是满足卷积的形式的
即((q_1,q_2,q_3,...)*(0,frac{1}{1^2},frac{1}{2^2},frac{1}{3^2},...))
证明。。。
考虑(f_3),卷积后的第三位上,为(frac{q_1}{2^2}+frac{q_2}{1^2})恰好是答案
所以FFT上啊
对于负贡献的话把(q)数组反过来即可
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
inline void read(int &x){
x=0;char ch;bool flag = false;
while(ch=getchar(),ch<'!');if(ch == '-') ch=getchar(),flag = true;
while(x=10*x+ch-'0',ch=getchar(),ch>'!');if(flag) x=-x;
}
inline int cat_max(const int &a,const int &b){return a>b ? a:b;}
inline int cat_min(const int &a,const int &b){return a<b ? a:b;}
const int maxn = 400010;
const double pi = acos(-1);
struct complex{
double x,y;
complex(){}
complex(double a,double b){x=a;y=b;}
complex operator + (const complex &r){return complex(x+r.x,y+r.y);}
complex operator - (const complex &r){return complex(x-r.x,y-r.y);}
complex operator * (const complex &r){return complex(x*r.x-y*r.y,x*r.y+y*r.x);}
complex operator / (const double &r){return complex(x/r,y/r);}
};
void FFT(complex *x,int n,int p){
for(int i=0,t=0;i<n;++i){
if(i > t) swap(x[i],x[t]);
for(int j=n>>1;(t^=j) < j;j >>= 1);
}
for(int m=2;m<=n;m<<=1){
complex wn(cos(p*2*pi/m),sin(p*2*pi/m));
for(int i=0;i<n;i+=m){
complex w(1,0),u;
int k = m>>1;
for(int j=0;j<k;++j,w=w*wn){
u = x[i+j+k]*w;
x[i+j+k] = x[i+j] - u;
x[i+j] = x[i+j] + u;
}
}
}
if(p == -1) for(int i=0;i<n;++i) x[i] = x[i]/n;
}
double q[maxn];
complex a[maxn],b[maxn],c1[maxn],c2[maxn];
int main(){
int n;read(n);
for(int i=0;i<n;++i) scanf("%lf",&q[i]);
int len ;
for(int i=1;(i>>2) < n;i<<=1) len = i;
// printf("%d
", len);
for(int i=0;i<n;++i){
a[i] = complex(q[i],0);
if(i != 0) b[i] = complex(1.0/i/i,0);
}
FFT(a,len,1);FFT(b,len,1);
for(int i=0;i<len;++i) c1[i] = a[i]*b[i];
memset(a,0,sizeof a);
for(int i=0;i<n;++i) a[i] = complex(q[n-i-1],0);
FFT(a,len,1);
for(int i=0;i<len;++i) c2[i] = a[i]*b[i];
//for(int i=0;i<n;++i) printf("%lf %lf || %lf %lf
",c1[i].x,c1[i].y,c2[i].x,c2[i].y);
FFT(c1,len,-1);FFT(c2,len,-1);
for(int i=0;i<n;++i) printf("%.3lf
",c1[i].x - c2[n-i-1].x);
getchar();getchar();
return 0;
}