【SinGuLaRiTy-1035】 Copyright (c) SinGuLaRiTy 2017. All Rights Reserved.
关于树链
树链是什么?这个乍一看似乎很陌生的词汇表达的其实就是在一棵树中从一个节点到另外一个节点的路径。在许多看似复杂的图论问题中,我们实际上只要对其进行适当的处理,把图转化为一棵树,问题就会得到化简,再运用树链的相关思想就可以较为轻松地解决。
树上倍增
所谓的“树上倍增”,其实就是一种记录节点的方法。我们定义一个数组f[i][j],表示节点i的第2^j个祖先(通常认为节点i的父亲为节点i的第一个祖先)。假设总共有n个节点,我们很容易看出,对这个数组中的i进行枚举的时间复杂度为O(n),而对j进行枚举的时间复杂度就要小得多了,才O(logn)。
对于一个树形结构,我们可以在O(nlogn)的时间内处理出f[][]数组:(与平常不同,由于递推式只涉及更小的j,只需要在外层枚举j,内层枚举i)
for(int i=1;i<=n;i++) f[i][0]=father[i]; for(int j=1;j<=LOG;j++)//这里的LOG表示常数log(n),通常取值为20左右 for(int i=1;i<=n;i++) f[i][j]=f[f[i][j-1]][j-1];
这个代码应该还是比较好理解的:f[i][0]表示的就是节点i的第(2^0=1)个祖先,也就是i的父亲;节点i的第2^j个祖先也就是节点i的第2^(j-1)个祖先的第2^(j-1)个祖先,因为2^(j-1)+2^(j-1)=2^j。(好吧,可能有点绞,来画一个图)。
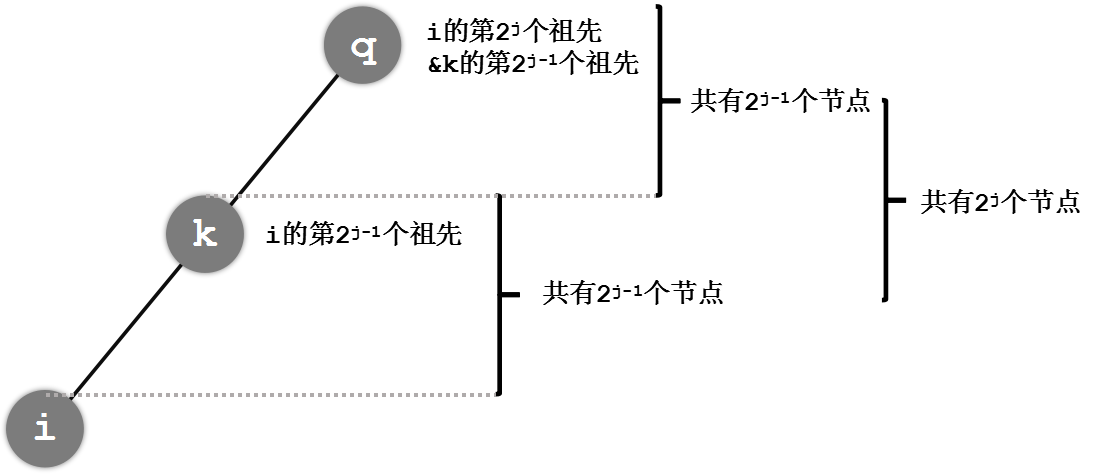
那么,我们如何利用f[][]数组快速定位节点x的第k个祖先呢?倍增数组要求一次只能向上跳2的整数次幂个节点,我们可以根据这一性质将k拆成一个二进制数,再通过2的次幂凑出k。代码如下:
int getk(int x,int k) { for(int i=0;i<LOG;i++ if(k&(1<<i)) x=f[x][i]; return x; }
那么如果问题变成求x的深度为d的祖先呢?(深度,若一个节点的第a个祖先为根节点,那么这个节点的深度就为a) 其实也很简单,只要稍微变换一下就可以变为上面的问题:
int getd(int x,int d) { return getk(x,dep[x]-d); }
最近公共祖先问题(LCA)
什么是最近公共祖先?对于有根树的任意两个节点u,v,u和v的共有祖先中深度最大(离根最远)的节点被称为u和v的最近公共祖先。
那么怎么求两个节点的最近公共祖先呢?我们可以通过这两个节点到根节点的路径来判断。如下图,假设我们要求节点4和节点5的最近公共祖先,我们发现它们到根节点的路径分别为4-3-2-1和5-2-1,于是我们可以从后往前同时对这两个路径进行遍历:它们的最后一个路径点相同,倒数第二个路径点也相同,但是到倒数第三个就不同了,于是我们把最后一组相同的节点作为最近公共祖先——节点2就是节点4和节点5的最近公共祖先。但是,这个过程有点复杂了:先要得到两个节点到根节点的路径再倒回来往回找,于是我们可以对这个过程进行优化。在计算路径之前,我们先同意这两个节点的深度:节点4的深度为3,节点5的深度为2,于是我们把节点4往上移到节点3,使两个节点的深度一致,转而求节点3与节点5的最近公共祖先(这个操作肯定不会影响结果)。这样一来,我们同时对两个节点进行路径计算,他们的第一对相同的路径点(依然是节点2)即为最近公共祖先。
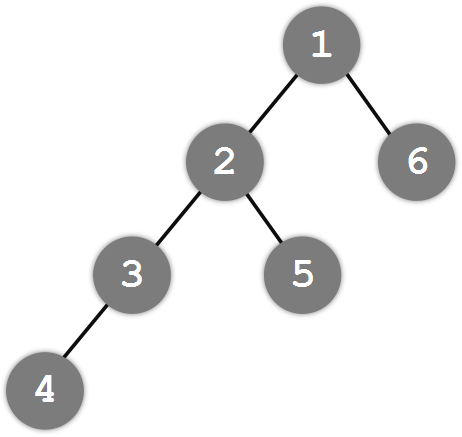
其实,我们可以直接用倍增数组查找最近公共祖先。(以下代码实际上求的是最近公共祖先之下的两个节点,最近公共祖先为father[u]和father[v])
for(i=LOG-1;i=0;i--) if(f[u][i]!=f[v][i]) u=f[u][i], v=f[v][i];
在进入这段代码之前,要对u和v进行特判:若u=v,那么这个点本身就是所求的最近公共祖先;若u!=v,再进入代码求解。
一些模板题
洛谷 P3019 Meet Place 会见点 (USACO 2011 Mar-Silver)
COGS 1588 Distance Queries 距离咨询 (USACO 2004 Feb-Gold)
路径最值查询问题
【NOIP2013】货车运输
有 n 座城市,编号从 1 到 n,城市之间有 m 条双向道路。每一条道路对车辆都有重量限制,简称限重。现在有 q 辆货车在运输货物,每辆车有自己的起点城市和终点城市,司机们想知道每辆车在不超过限重的情况下,最多能运多重的货物。(可认为n,m,q都是10万)
思路:求出图的最大生成树, 易知两点在最大生成树上的路径最小値等价于原图中的瓶颈边的权値。记f[i][j]表示节点i的第2^j个祖先。另开一个数组g[i][j]表示节点i到第2^j个祖先最小值.。这两个数组均通过递推求得。在倍增法求LCA的过程中.同步记录路径最小值即可,也就是说, 每一次执行x=f[x][i]操作,同步记录ans=min(ans,g[x][i])。时间复杂度0((n+m)logn)。
<这题到处都有,就不贴代码了>
【CQBZOJ】避难向导 (2015年重庆多校NOIP模拟联考)
给定一棵n个节点的树,点带权 m次询问,求从a走到b,遇到的第一个点权不低于w的节点的编号,不存在输出-1 (n≤10w, m≤30w)
思路一:设c=LCA(a,b),我们将一个路径拆解成a->c, c->b两部分.这样的好处是每一部分都是一条祖先一后代的直链,,由于需要求离a最近的点.所以原问题被拆成了两个子任务:从一个点到它的某个祖先这条链上离这个点最近/最远的权值不低于w的点。记f[i][j]为祖先数组,g[i][j]表示距离节点i最近的2^j个祖先中最大的点权。显然可以通过二分深度来完成这两个子任务。复杂度0(m1og^2n)无法通过全部数据。
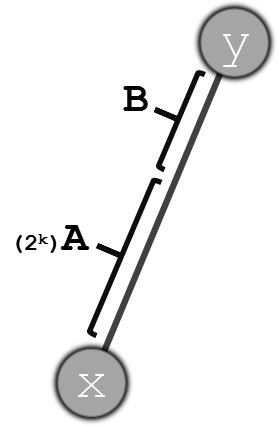
思路二:如图,将一条x-y的直链看成A和B两部分:A中包含2的整数次幂个节点,且A的长度大于x-y总长度的1/2;其余的部分为B。通过这样的思路来考察上述两个子任务:
一、离x最近的:
知道k时,可以O(1)判断答案是否在A中。 ① 如果在A中,枚举i从k-1到0即可得到答案。 ② 如果A中不存在合法解,则令x=f[x][k],递归进行以上过程。 对于①,整个递归过程中只有得出答案前会被执行一次。 对于②,每次递归后k的值减少,而k上界为logn,下界为0,所以递归深度为O(logn) 综上。该操作复杂度为O(logn)。
二、离x最远的:
① 优先令x=f[x][k],递归在B段中求解。如递归返回后已经得到答案,则直接返回答案。 ② 如经过①没有获得答案,则O(1)检查A段中是否有答案,如果没有,则x-y整段路径中无解。如果有,则枚举i从k-1到0即可定位答案。 类似子任务一,该部分的复杂度为O(logn)。
Code

#include<cstdio> #include<algorithm> #include<cmath> #include<cstdlib> #include<iostream> #include<cstring> using namespace std; #define MAXN 100010 #define LOG 18 int Log,n,m,l[MAXN],f[MAXN][2],ms[MAXN],t,a,b,c,x,y,qi,g[MAXN],s[MAXN],ans,fa[MAXN],p[MAXN][LOG],mx[MAXN][LOG]; void Read(int &x){ char c; while(c=getchar(),c!=EOF) if(c>='0'&&c<='9'){ x=c-'0'; while(c=getchar(),c>='0'&&c<='9') x=x*10+c-'0'; ungetc(c,stdin); return; } } struct node { int v,wt; node *next; }edge[MAXN*2],*adj[MAXN],*ecnt=edge; void add(int u,int v,int wt) { node *p=++ecnt; p->v=v; p->wt=wt; p->next=adj[u]; adj[u]=p; } void dfs1(int u){ int v; for(node *p=adj[u];p;p=p->next) { v=p->v; if(v==fa[u]) continue; fa[v]=u; l[v]=l[u]+1; dfs1(v); if(f[v][0]+p->wt>f[u][0]) { f[u][1]=f[u][0]; f[u][0]=f[v][0]+p->wt; ms[u]=v; } else if(f[v][0]+p->wt>f[u][1]) f[u][1]=f[v][0]+p->wt; } } void dfs2(int u,int wt) { if(ms[fa[u]]==u) g[u]=f[fa[u]][1]; else g[u]=f[fa[u]][0]; g[u]=max(g[u],g[fa[u]])+wt; for(node *p=adj[u];p;p=p->next) if(p->v!=fa[u]) dfs2(p->v,p->wt); } void prepare() { int i,j; for(i=1;i<=n;i++) { p[i][0]=fa[i]; mx[i][0]=s[fa[i]]; } for(j=1;j<=Log;j++) for(i=1;i<=n;i++) { p[i][j]=p[p[i][j-1]][j-1]; mx[i][j]=max(mx[i][j-1],mx[p[i][j-1]][j-1]); } } int lca(int x,int y) { int i; if(l[x]<l[y]) swap(x,y); for(i=Log;i>=0;i--) if(l[x]-(1<<i)>=l[y]) x=p[x][i]; if(x==y) return x; for(i=Log;i>=0;i--) if(p[x][i]!=p[y][i]) x=p[x][i],y=p[y][i]; return fa[x]; } int find1(int x,int d,int a) { if(l[x]<=l[a]) return -1; for(;l[p[x][d]]<l[a]&&d>=0;d--); if(mx[x][d]<qi) return find1(p[x][d],d-1,a); for(int i=d-1;i>=0;i--) if(mx[x][i]<qi) x=p[x][i]; return fa[x]; } int find2(int x,int d,int a) { int i,ret; if(l[x]<=l[a]) return -1; for(;l[p[x][d]]<l[a]&&d>=0;d--); ret=find2(p[x][d],d-1,a); if(~ret) return ret; if(mx[x][d]<qi) return -1; for(i=d-1;i>=0;i--) if(mx[p[x][i]][i]>=qi) x=p[x][i]; return fa[x]; } int main() { int i,u,v,wt; Read(n),Read(m),Read(a),Read(b),Read(c); for(Log=0;1<<Log<=n;Log++); Log--; for(i=1;i<n;i++) { Read(u),Read(v),Read(wt); add(u,v,wt); add(v,u,wt); } dfs1(1); dfs2(1,0); for(i=1;i<=n;i++) s[i]=((long long)max(f[i][0],g[i])+a)*b%c; prepare(); while(m--) { Read(x),Read(y),Read(qi); int d,a=lca(x,y); ans=-1; if(s[x]>=qi) ans=x; if(ans==-1) { for(d=0;1<<d<=l[x];d++); d--; ans=find1(x,d,a); } if(ans==-1) { for(d=0;1<<d<=l[y];d++); d--; ans=find2(y,d,a); } if(ans==-1&&s[y]>=qi) ans=y; printf("%d ",ans); } return 0; }
轻重链剖分
在开始之前,我们需要了解以下的术语:
重儿子:对于一个父亲节点来说,其子树大小最大的儿子。
重边(图中的粗边):连接父亲节点和重儿子的边。 轻边:重边以外的边。
重链:重边形成的链。需要注意的是:没有连接重边的节点自成一条仅包含这个节点本身的重链(例如节点12)。
还有一些记号,我们会经常提到:
siz[x]:节点x的子树大小,如siz[2]=5
son[x]:节点x的重儿子,如son[1]=4
top[x]:节点x所在重链顶端的节点,如top[11]=2, top[12]=12, top[13]=1
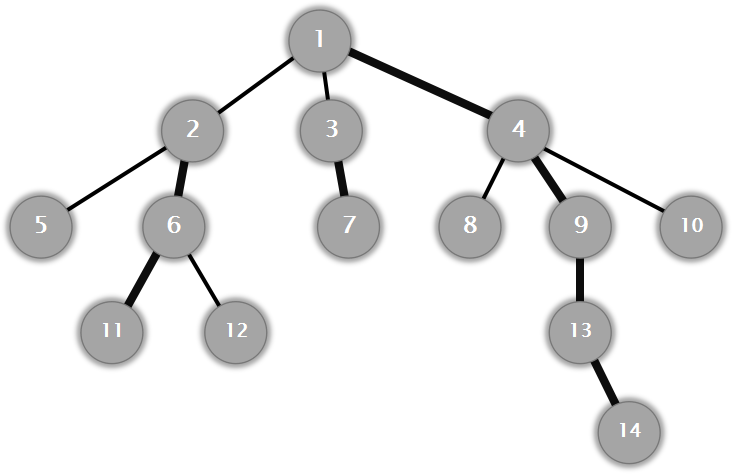
那么,如何用代码来实现轻重链剖分的过程呢?以下是伪代码:
void dfs1(u) { siz[u]=1; for(v是u的儿子) { dfs1(v); siz[u]+=siz[v]; if(siz[v]>siz[son[u]]) son[u]=v; } } void dfs2(u) { if(son[u]) top[son[u]]=top[u],dfs2(son[u]); for(v是u的儿子且v!=son[u]) { top[v]=v; dfs2(v); } } int main() { dfsl(1),top[1]=1,dfs2(1); }
另外,还要补充一点性质:从任何一个节点一直往上走到根,遇到的轻边为O(logn)级别(证明:轻边的两端点的子树点数之差至少为2倍)。我们甚至可以发现:轻边数量的nlogn的常数级别实际上是非常小的。
由此,树链剖分就有了多种应用:
求最近公共祖先
定义dep[x]表示x的深度,如dep[1]=1, dep[7]=3。
int lca(int u,int v) { while(top[u]!=top[v]) { if(dep[top[u]]>dep[top[v]]) u=fa[top[u]]; else v=fa[top[v]]; } return dep[u]<dep[v] ? u:v; }
假设v是u的祖先,求既是u的祖先也是v的儿子的点
int getlow(int u,int v) { while(top[u]!=top[v]) { if(fa[top[u]]==v) return top[u]; u=fa[top[u]]; } return son[v]; }
求一个点的祖先中深度为d的点
根据dfs2的代码实现,可以得出同一条重链上的所有点在dfs2的dfs序列中一定是连续的。记dfn[x]表示节点x是第几个被遍历到的节点;记id[x]表示第x个遍历到的节点是谁。只需在dfs2函数体内部将语句id[dfn[u]=++tmr]=u加在第一行即可。
int find(int u,int d) { while(dep[top[u]]>d) u=fa[top[u]]; return id[dfn[u]-(dep[u]-d)]; }
一些例题
HDU 5452 Minimum Cut (2015 ACM/ICPC 亚洲区沈阳站网络赛)
[补充] 另类桥边(割/割边)算法
割边的定义:对于一个无向图,如果去掉其中某一条边后整个图变成完全分隔两个图,则该边称为割边。割边不在任何环中。
以任意顺序保存边,然后做一次并查集优化的生成树。所有割边一定存在于任何一棵生成树中。
再一次访问保存边的数组,忽略已经在生成树中的边。对于其他某条边,它的出现一定会使生成树上产生一个环,这个环中的边显然都不是割边,于是将这条路径的覆盖次数+1。
求出子树和,覆盖次数为0的边集就是割集。
一些例题
轻重链剖分小结
链剖实际运行速度非常快,可直接替代tarjan离线lca。
| 空间复杂度 | 预处理复杂度 | 单次询问复杂度 | |
| 倍增 | O(nlogn) | O(nlogn) | O(logn) |
| 链剖 | O(n) | O(n) | O(nlogn) |
另一类问题:Kruskal树
(在关于Kruskal的讨论中,我们以最小生成树为例。)
我们都会用Kruskal算法来求最小生成树:将边按权值排序,顺序加边,并用并查集维护连通性。
下面,我们对这个算法进行些许的改进:将边视为额外的点,合并两个集合时,将边对应的点作为新的祖先,这样就生成了Kruskal树。它的高度最坏是O(n),但我们还可以进行优化:我们发现,我们事实上只需要访问它的根节点,因此,我们可以用并查集的路径压缩进行优化。
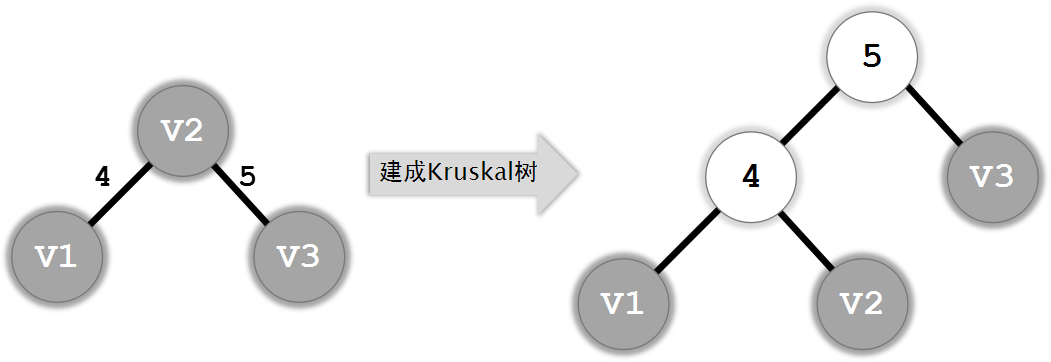
生成的Kruskal树有以下定理:
定理一:Kruskal树是一棵二叉树(因为边一定只连接2个点),树中叶子节点为原来的节点,其它节点是原来的边。
定理二:在最小生成树的例子中,从叶子到根的路径中,点权递增。
定理三:两个叶子节点的LCA的权值为原图中两点之间的瓶颈边。
又是一些例题
再来最后一个例题:过去的集合
(原题找不到了,只能写出大致的题意)
有n个点,初始时刻每个点单独为一个集合。支持两个操作:将点x和点y所在集合合并。查询第k次合并操作前,点a和点b是否在一个集合中。
n≤1000000,强制在线
思路:
利用Kruskal树,边权设置为操作编号。由于按照添加边的顺序边权依次递增,满足Kruskal算法的性质。 查询时,如果到目前为止两个点不同根,则答案肯定是no。 如果同根,则查询两个点的LCA的权值,若该权值小于k,则答案为yes,否则为no。 两点间瓶颈边为从a到b所必经的权值最大的边,在本题中对应最后添加的边。
可惜的是,使用路径压缩实现的Kruskal树在构造完之前,是无法支持快速查询LCA的。 如果支持离线操作,可以执行完所有合并操作之后再执行查询。 考虑使用Kruskal树的瓶颈是什么? 每一次合并必须新建一个节点,导致树高无法控制。
在两个节点之间建立一个有权值的节点,等价于在这两个节点之间连接一条有权值的边。 给并查集的边赋上边权,表示这是第几次添加的边。 使用按秩合并优化,则树高可以控制在log级别。 两个节点在并查集中的路径最大值等于这两个节点的连通时间,也就是Kruskal树中LCA的权值。 并查集高度为O(logn),此时可以暴力求LCA。
关于该题中的并查集优化——按秩合并
不加优化地直接合并并查集,单次操作复杂度可能达到O(n)。当并查集的边具有边权时,路径压缩可能会损失边的信息。
定义并查集的秩,记rnk[x]表示以x为根的树的高度(当x不是根时rnk[x]的值无意义且不会被访问)。合并时,将高度更大的树的根作为新的根。
以下为合并代码:
int find(int x) { if(fa[x]==x) return x; return find(fa[x]); } void unite(int x,int y) { x=find(x),y=find(y); if(rnk[x]>rnk[y]) swap(x,y); fa[x]=y; if(rnk[x]==rnk[y]) rnk[y]++; }
可以证明,按秩合并的并查集单次操作复杂度最坏为O(logn)。 路径压缩的并查集单次操作的复杂度最坏为O(n),当操作的次数达到O(n)级别时,均摊复杂度为O(logn)。
Time:2017-08-11
