[SinGuLaRiTy] 数论题目复习

[CQBZOJ 1464] Hankson

题目描述

Hanks博士是BT (Bio-Tech，生物技术) 领域的知名专家，他的儿子名叫Hankson。现在，刚刚放学回家的Hankson正在思考一个有趣的问题。今天在课堂上，老师讲解了如何求两个正整数c1和c2的最大公约数和最小公倍数。现在Hankson认为自己已经熟练地掌握了这些知识，他开始思考一个“求公约数”和“求公倍数”之类问题的“逆问题”，这个问题是这样的：

已知正整数a0,a1,b0,b1，设某未知正整数x满足：

1． x和a0的最大公约数是a1；

2． x和b0的最小公倍数是b1。

Hankson的“逆问题”就是求出满足条件的正整数x。但稍加思索之后，他发现这样的 x并不唯一，甚至可能不存在。因此他转而开始考虑如何求解满足条件的x的个数。请你帮助他编程求解这个问题。

输入

第一行为一个正整数n，表示有n组输入数据。接下来的n行每行一组输入数据，为四个正整数a0，a1，b0，b1，每两个整数之间用一个空格隔开。输入数据保证a0能被a1整除，b1能被b0整除。

输出

输出共n行。每组输入数据的输出结果占一行，为一个整数。对于每组数据：若不存在这样的x，请输出0；若存在这样的x，请输出满足条件的x的个数。

样例数据

样例输入	样例输出
2 41 1 96 288 95 1 37 1776	6 2

解析

∵lcm(x,b0)*gcd(x,b0)=x*b0
∴lcm(x,b0)=x*b0/gcd(x,b0)
又∵lcm(x,b0)=b1
∴x*b0/gcd(x,b0)=b1
即b1*gcd(x,b0)=x*b0
gcd(x,b0)=x*b0/b1
gcd[x/(x*b0/b1),b0/(x*b0/b1)]=x*b0/b1/(x*b0/b1)
得gcd(b1/b0,b1/x)=1
∴x为b1的约数，即x|b1
又∵由题意得：a1为x的约数，即x%a1=0
∵题目中有：① gcd(x,a0)=a1
② lcm(x,b0)=b1
∴由②得：gcd(b1/b0,b1/x)=1 ③
由①得：gcd(x/a1,a0/a1)=1 ④
由③④可对枚举进行优化.

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>

using namespace std; 

int cnt,tot;
int a0,a1,b0,b1;

int gcd(int a,int b)
{
    return b==0 ? a:gcd(b,a%b);
}

bool calculation(long long x)
{
    if(x%a1!=0)
        return 0;
    return gcd(x/a1,a0/a1)==1&&gcd(b1/b0,b1/x)==1;
} 

int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d%d%d",&a0,&a1,&b0,&b1);
        int ans=0;
        for(int i=1;i*i<=b1;i++)
        {
            if(b1%i==0)
            {
                ans+=calculation(i);
                if(b1/i!=i)
                    ans+=calculation(b1/i);
            }
        }
        printf("%d
",ans);
    }
    return 0；
}

[CQBZOJ 2642] 无平方因子的数

题目描述

给出正整数n和m，区间[n, m]内的“无平方因子”的数有多少个？整数p无平方因子当且仅当不存在 k > 1，使得p是k^2 的倍数。

输入

第1行：2个整数n和m (1 <= n <= m <= 10^9, m - n <= 10^7)

输出

第1行：1个整数，表示区间中无平方因子的数的个数Cnt

样例数据

样例输入	样例输出
1 10	7

解析

可以在区间[n,m]中for循环筛选出有平方因子的数，做到这一点很简单：对于每一个平方因子数k*p*p，只需枚举k，p，循环(可进行一些小优化)途中进行计数，最后用区间内的总个数减去有平方因子的数就可以得到答案了。

Code

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cstring>
bool v[10000002];
int p[10000010];
int k;
void Prime(int n)
{
    for(int i=2;i<=n;i++)
    {
        if(!v[i]) 
            p[++k]=i;
        for(int j=1;j<=k&&p[j]*i<=n;j++)
        {
            v[i*p[j]]=1;
            if(i%p[j]==0) 
                break;
        }
    }
    memset(v,0,sizeof(v));
}
int main()
{
    int n,m,s=0;
    scanf("%d%d",&n,&m);
    Prime(30000);
    for(int i=1;p[i]*p[i]<=m;i++)
        for(int j=p[i]*p[i];j<=m;j+=p[i]*p[i])
            if(j>=n&&!v[j-n]) 
                v[j-n]=1,s++;
    printf("%d",m-n+1-s);
    return 0;
}

[POJ 2407] 欧拉函数的值

题目描述

给定整数n，求n的欧拉函数的值。

输入

多组数据

每行一个整数，表示n( 1 <= n <= 1,000,000,000)；一个0，表示输入结束

输出

每行输入一个整数，表示对应的n的欧拉函数值

样例数据

样例输入	样例输出
7 12 0	6 4

解析

似乎对欧拉函数已经有些陌生了：不超过n且与n互质的正整数。

对于求解欧拉函数，似乎并没有什么便于理解的逻辑推理，只有背板了。

Code

#include<iostream>
#include<cmath>
using namespace std;
int main()
{
    int n,i,temp;
    while(scanf("%d",&n)!=EOF)
    {
        temp=n;
        for(i=2;i*i<=n;i++)
        {
          if(n%i==0)
          {
              while(n%i==0) n=n/i;
              temp=temp/i*(i-1);
          }
          if(n<i+1)
              break;
        }
        if(n>1)
            temp=temp/n*(n-1);
        printf("%d
",temp);
    }
    return 0;
}

[CQBZOJ 2948] 质数密度

题目描述

我们定义区间[L, R]的质数密度为区间中质数的个数除以区间中数的个数。例如，区间[1,10]中的质数有2,3,5,7这4个，所以质数密度为4 / 10 = 0.4

给出区间的左、右端点，请计算出区间的质数密度。

输入

第1行：2个整数L, R，表示区间的左、右端点(1<=L < R <= 10^5)

输出

第1行：1个浮点数，表示答案。结果保留7位小数。

样例数据

样例输入	样例输出
1 10	0.400000

解析

需运用线性筛素数。基本思路为：先假设所有的数都是素数，运用“所有素数乘一个不为1的整数都为合数”这一定理，将得到的合数一一筛去。当然，在该算法的基础上有多种优化。

这里有一篇不错的写线性筛素数法的文章：[一般筛法求素数+快速线性筛法求素数]

Code

#include<cstdio>
#include<cmath>
using namespace std;
int main()
{
    int L,R,m,cnt=0;
    double ans;
    bool flag;
    scanf("%d%d",&L,&R);
    for(int i=(L==1)?2:L;i<=R;i++) {
        m=(int)(sqrt(i)+0.5);
        flag=true;
        for(int j=2;j<=m;j++)
            if(i%j==0)
            {
                flag=false;
                break;
            }
        if(flag)
            cnt++;
    }
    ans=1.0*cnt/(R-L+1);
    printf("%.7f
",ans);
    return 0;
}

[USACO 3.2.1] 阶乘

题目描述

N的阶乘写作N!表示小于等于N的所有正整数的乘积。阶乘会很快的变大，如13!就必须用32位整数类型来存储，70！即使用浮点数也存不下了。

你的任务是找到阶乘最后面的非零位。

举个例子: 5!=1*2*3*4*5=120所以5!的最后面的非零位是2 7！=1*2*3*4*5*6*7=5040，所以最后面的非零位是4.

输入

共一行，一个整数不大于4，220的整数N。

输出

共一行，输出N!最后面的非零位。

样例数据

样例输入	样例输出
7	4

解析

要解这道题，首先就要知道末尾的零是如何产生的：

1>末尾分别为5和2的数相乘会得到“0”;

2>乘10的倍数时会得到“0”;

现在，我们一旦将这些数（注意：只有2与5成对出现时才可以抵消，单出来的不能剔除）剔除出去，再不断相乘，对乘积保留末尾的数，再将其乘起来......乘完了所有的数，答案也就得出来了。

（当然，也可以对乘积不断模10，这实际上也实现了上述操作）。

Code

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
int main()
{
    int n,ans=1;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        ans=(ans*i)%1000000;
        while(ans%10==0) 
            ans=ans/10;
    }
    printf("%d",ans%10);
    return 0;
}

[POJ 1845] 幂的约数之和

题目描述

给定正整数A, B，求A^B的所有因数之和，并模9901。

输入

仅一行，有两个整数A和B(0 <= A,B <= 50000000)。

输出

输出仅一行：问题的答案。

样例数据

样例输入	样例输出
2 3	15

解析

要求的是A^B的所有因子的和之后再mod 9901的值。

因为一个数A能够表示成多个素数的幂相乘的形式。即A=(a1^n1)*(a2^n2)*(a3^n3)...(am^nm)。

所以这个题就是要求(1+a1+a1^2+...a1^n1)*(1+a2+a2^2+...a2^n2)*(1+a3+a3^2+...a3^n2)*...(1+am+am^2+...am^nm) mod 9901。

对于每一个(1+a1+a1^2+...a1^n1) mod 9901 ，等于 (a1^(n1+1)-1)/(a1-1) mod 9901，这里用到逆元的知识：a/b mod c = (a mod (b*c))/ b

所以就等于(a1^(n1+1)-1)mod (9901*(a1-1)) / (a1-1)。

至于前面的a1^(n1+1)，快速幂。

Code

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#define LL long long
using namespace std;
const int mod=9901;
int A,B;
LL ans=1;
LL ksm(LL a,LL b)
{
    LL s=1,tmp=a;
    while(b)
    {
        if(b%2)
            s=s*tmp%mod;
        tmp=tmp*tmp%mod;
        b>>=1;
    }
    return s;
}
LL sum(LL a,LL b)
{
    if(!a)
        return 0LL;
    if(!b)
        return 1LL;
    if(b&1)
        return ((1+ksm(a,b/2+1))%mod*sum(a,b/2)%mod)%mod;
    return ((1+ksm(a,b/2+1))%mod*sum(a,b/2-1)+ksm(a,b/2)%mod)%mod;
}
void get(int num)
{
    LL prnow=0LL;
    LL now=0LL;
    for(int i=2;i<=num;i++,now=0LL)
    {
        while(num%i==0)
        {
            num/=i;
            now+=1;
        }
        now*=B;
        prnow=sum(i,now);
        ans=ans*(prnow%mod)%mod;
    }
    return ;
}
int main()
{
    scanf("%d%d",&A,&B);
    get(A);
    printf("%lld
",ans);
    return 0;
}

[HDU 1576] A/B

题目描述

要求(A/B)%9973，但由于A很大，我们只给出n(n=A%9973)(我们给定的A必能被B整除，且gcd(B,9973) = 1)。

输入

数据的第一行是一个T，表示有T组数据。
每组数据有两个数n(0 <= n < 9973)和B(1 <= B <= 10^9)。

输出

对应每组数据输出(A/B)%9973。

样例数据

样例输入	样例输出
2 1000 53 87 123456789	7922 6060

解析

设(A/B)%9973=K
则A/B=K+9973x (x为未知整数)
∴A=KB+9973*B*x
又∵A%9973=n
∴KB%9973=n
∴KB=n+9973y(y为未知整数)
∴(K/n)*B+(-y/n)*9973=gcd(B,9973)=1
由此：通过exgcd()求出K/n，再乘n，最后取模，即得到答案。

忘记了扩展欧几里得？

void exgcd(LL a,LL b,LL &d,LL &x,LL &y)
{
    if(!b)
    {
        x=1;
        d=a;
        y=0;
    }
    else 
    {
             exgcd(b,a%b,d,y,x);
             y-=x*(a/b);
    }
}
//x即为a的逆元。

Code

#include<cstdio>
#include<cstdlib>

#define m 9973

using namespace std;

void exgcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1,y=0;
        return ;
    }
    exgcd(b,a%b,x,y);
    int r=x;
    x=y;
    y=r-(a/b)*y;
}

int main()
{
    int n,b,t,x,y;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&b);
        exgcd(b,m,x,y);
        x=(x%m+m)%m;
        printf("%d
",(x*n)%m);
    }
    return 0;
}

[HDU 2462] The Luckiest Number

题目描述

Chinese people think of '8' as the lucky digit. Bob also likes digit '8'. Moreover, Bob has his own lucky number L. Now he wants to construct his luckiest number which is the minimum among all positive integers that are a multiple of L and consist of only digit '8'.

输入

The input consists of multiple test cases. Each test case contains exactly one line containing L(1 ≤ L ≤ 2,000,000,000).
The last test case is followed by a line containing a zero.

输出

For each test case, print a line containing the test case number( beginning with 1) followed by a integer which is the length of Bob's luckiest number. If Bob can't construct his luckiest number, print a zero.

样例数据

样例输入	样例输出
8 11 16 0	Case 1: 1 Case 2: 2 Case 3: 0

解析

这道题现在只隐隐约约想到快速幂，但实在是想不起来解法。于是看了看题解：

首先，由题意可以得出，(10^x-1)/9*8=L*p(p是一个未知数，但必定是整数)。
然后对上式进行移项处理，得：(10^x-1)=9*L*p/8。
设m=9*L/gcd(L,8)，则有(10^x - 1) = m*p’。p’是必然存在的一个整数。
然后问题就转化成为了10^x=1(mod m)，观察此式，显然，m和10必定互质。
于是根据欧拉定理，10^(Euler(m))=1(mod m)。由于题目要求最小的解，解必然是Euler(m)的因子。
需要注意的是，对于10^x，由于m太大，直接快速幂相乘的时候会超long long......好bug，需要乘法转化一下。

Code

#include <vector>
#include <cstdio>
#include <iostream>
#include <algorithm>
#define LL long long
#define MAXN 400010
using namespace std;
bool vis[MAXN];
vector<LL> hav;
vector<int> prime;

LL gcd(LL a,LL b)
{
    return b==0 ? a : gcd(b, a%b);
}

void gen_primes()
{
    for(int i=2;i<MAXN;++i)
        if(!vis[i])
        {
            prime.push_back(i);
            if(i<1111)
                for(int j=i*i;j<MAXN;j+=i)
                    vis[j]=true;
        }
    return ;
}

LL euler_phi(LL n)
{
    LL ans=n;
    for(int i=0;(LL)(prime[i]*prime[i])<=n; ++i)
    {
        if(n%prime[i]==0)
        {
            ans=ans/prime[i]*(prime[i]-1);
            n/=prime[i];
            while(n%prime[i]==0)
                n/=prime[i];
        }
    }
    if(n>1)
        ans=ans/n*(n-1);
    return ans;
}

LL Mul(LL a,LL b,LL c)
{
    LL ans=0;
    while(b)
    {
        if(b&1)
            ans=(ans+a)%c;
        a=a*2%c;
        b>>=1;
    }
    return ans;
}

LL Pow(LL a,LL b,LL c)
{
    LL ans=1;
    while(b)
    {
        if(b&1)
            ans=Mul(ans,a,c);
        a=Mul(a,a,c);
        b>>=1;
    }
    return ans;
}

void get_hav(LL n)
{
    hav.clear();
    for(int i=0;i<prime.size()&&n>1;++i)
    {
        while(n%(LL)prime[i]==0)
        {
            n/=prime[i];
            hav.push_back(prime[i]);
        }
    }
    if(n>1)
        hav.push_back(n);
}

int main()
{
    LL n,m,x,cas=1;
    gen_primes();
    while(cin>>n&&n)
    {
        m=9*n/gcd(n,8LL);
        if(gcd(m,10LL)!=1)
        {
            cout<<"Case "<<cas++<<": 0"<<endl;
            continue;
        }
        x=euler_phi(m);
        get_hav(x);
        for(int i=0;i<hav.size();++i)
        {
            if(Pow(10LL,x/hav[i],m)==1)
                x/=hav[i];
        }
        cout<<"Case "<<cas++<<": "<<x<<endl;
    }
    return 0;
}

[HDU 3307] Description Has Only Two Sentences

题目描述

a_n = X*a_n-1 + Y and Y mod (X-1) = 0.
Your task is to calculate the smallest positive integer k that a_k mod a₀ = 0.

输入

Each line will contain only three integers X, Y, a₀ ( 1 < X < 2³¹, 0 <= Y < 2⁶³, 0 < a₀ < 2³¹).

输出

For each case, output the answer in one line, if there is no such k, output "Impossible!".

样例数据

样例输入	样例输出
2 0 9	1

解析

∵an=x*an-1+Y
∴an+A=x*an-1+Y+A
∴an+A=x(an-1+(Y+A)/x)
令A=(Y+A)/X
∴(X-1)*A=Y
即A=Y/(X-1)
∴{an+A}是等比数列
∴an/a0=X^n+P*(X^n-1)/a0
转换成X^n%(a0/p)=1，发现该式符合欧拉定理,
所以由x^n组成的集合是个循环群,phi(a/p)是循环节,而且最小循环节必定是phi(a/p)的因数.

<欧拉定理>

欧拉定理：若a与m互质，则。

Code

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>

using namespace std;

typedef long long lld;

lld gcd(lld a,lld b)
{
    if(!b)
        return a;
    else
        return gcd(b,a%b);
}

lld Min(lld a,lld b)
{
    return (a<b)?(a):(b);
}

lld phi(lld n)
{
    lld ans=n;
    lld lim=sqrt(n);
    for(int i=2;i<=lim;i++)
    {
        if(n%i==0)
        {
            ans=ans*(i-1)/i;
            while(n%i==0)
                n/=i;
        }
    }
    if(n>1)
        ans=ans*(n-1)/n;
    return ans;
}

lld x,y,a0,ap;

lld qpow(lld a,lld b)
{
    lld ans=1;
    while(b)
    {
        if(b&1)
            ans=(ans*a)%ap;
        a=a*a%ap;
        b>>=1;
    }
    return ans%ap;
}

int main()
{
    while(~scanf("%I64d%I64d%I64d",&x,&y,&a0))
    {
        lld p=y/(x-1);
        lld gcds=gcd(a0,p);
        ap=a0/gcds;
        if(gcd(x,ap)!=1)
        {
            puts("Impossible!");
            continue;
        }
        lld ans=phi(ap);
        lld Lim=ans;
        for(int i=2;i<=sqrt(Lim);i++)
            if(Lim%i==0)
            {
                if(qpow(x,i)==1)
                    ans=Min(ans,i);
                if(qpow(x,Lim/i)==1)
                    ans=Min(ans,Lim/i);
            }
        printf("%I64d
",ans);
    }
    return 0;
}

[HDU 1452] Happy 2004

题目描述

Consider a positive integer X,and let S be the sum of all positive integer divisors of 2004^X. Your job is to determine S modulo 29 (the rest of the division of S by 29).
Take X = 1 for an example. The positive integer divisors of 2004^1 are 1, 2, 3, 4, 6, 12, 167, 334, 501, 668, 1002 and 2004. Therefore S = 4704 and S modulo 29 is equal to 6.

输入

The input consists of several test cases. Each test case contains a line with the integer X (1 <= X <= 10000000).
A test case of X = 0 indicates the end of input, and should not be processed.

输出

For each test case, in a separate line, please output the result of S modulo 29.

样例数据

样例输入	样例输出
1 10000 0	6 10

解析

gcd(a,b)==1 && s(a,b)==s(a)*s(b)满足这种条件的s叫做积性函数，本题求的因子和就是一个积性函数；
接着有一个结论：
if(prime[p]) s(p^n)=1+p^1+p^2+p^n=(p^(n+1)-1)/(p-1)
s(2004^n)=s(2^(2n))*s(3^n)*s(167^n)
其中，167和22关于29同余
所以，s(2004^n)=s(2^(2n))*s(3^n)*s(2^n)
a=s(2^(2n))=(2^(2n+1)-1)
b=s(3^n)=(3^(n+1)-1)/2
c=s(22^n)=(22^(n+1)-1)/21
数太大，每步求余，除法求余的规则是，除以一个数求余的结果和乘以除数的乘法逆元的求余结果相同
求出2和21的乘法逆元这道题就做完了

Code

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#define LL long long
using namespace std;
const int mod=29;
int A=2004,B;
LL ans=1;
LL ksm(LL a,LL b)
{
    LL s=1,tmp=a;
    while(b)
    {
        if(b%2)
            s=s*tmp%mod;
        tmp=tmp*tmp%mod;
        b>>=1;
    }
    return s;
}
LL sum(LL a,LL b)
{
    if(!a)
        return 0;
    if(!b)
        return 1;
    if(b&1)
        return ((1+ksm(a,b/2+1))%mod*sum(a,b/2)%mod)%mod;
    return ((1+ksm(a,b/2+1))%mod*sum(a,b/2-1)+ksm(a,b/2)%mod)%mod;
}
void get(int num)
{
    LL prnow=0;
    LL now=0;
    for(int i=2;i<=num;i++,now=0LL)
    {
        while(num%i==0)
        {
            num/=i;
            now+=1;
        }
        now*=B;
        prnow=sum(i,now);
        ans=ans*(prnow%mod)%mod;
    }
    return ;
}
int main()
{
    for(;;)
    {
        scanf("%d",&B);
        if(B==0)
            return 0;
        get(A);
        printf("%I64d
",ans);
        ans=1;
    }
}

[POJ 1061] 青蛙的约会

题目描述

两只青蛙在网上相识了，它们聊得很开心，于是觉得很有必要见一面。它们很高兴地发现它们住在同一条纬度线上，于是它们约定各自朝西跳，直到碰面为止。可是它们出发之前忘记了一件很重要的事情，既没有问清楚对方的特征，也没有约定见面的具体位置。不过青蛙们都是很乐观的，它们觉得只要一直朝着某个方向跳下去，总能碰到对方的。但是除非这两只青蛙在同一时间跳到同一点上，不然是永远都不可能碰面的。为了帮助这两只乐观的青蛙，你被要求写一个程序来判断这两只青蛙是否能够碰面，会在什么时候碰面。
我们把这两只青蛙分别叫做青蛙A和青蛙B，并且规定纬度线上东经0度处为原点，由东往西为正方向，单位长度1米，这样我们就得到了一条首尾相接的数轴。设青蛙A的出发点坐标是x，青蛙B的出发点坐标是y。青蛙A一次能跳m米，青蛙B一次能跳n米，两只青蛙跳一次所花费的时间相同。纬度线总长L米。现在要你求出它们跳了几次以后才会碰面。

输入

输入只包括一行5个整数x，y，m，n，L，其中x≠y < 2000000000，0 < m、n < 2000000000，0 < L < 2100000000。

输出

输出碰面所需要的跳跃次数，如果永远不可能碰面则输出一行"Impossible"

解析

读完题目，首先可根据题意列出方程：k*a+t*l=b ，接着用exgcd()解方程......

当然，这道题还是没有那么水的，用exgcd求解的过程实际上比较复杂 [具体解析]

Code

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define LL long long
LL gcd(LL a,LL b)
{
    return b==0?a:gcd(b,a%b);
}
void gcdd(LL a,LL b,LL &x,LL &y)
{
    if(b==0)
    {
        x=1;
        y=0;
    }
    else
    {
        gcdd(b,a%b,y,x);
        y-=x*(a/b);
    }
}
int main()
{
    LL x,y,m,n,L;
    LL a,c,k1,k2,r;
    scanf("%I64d%I64d%I64d%I64d%I64d",&x,&y,&m,&n,&L);
    a=n-m;
    c=x-y;
    r=gcd(a,L);
    if(c%r)
    {
        printf("Impossible");
        return 0;
    }
    a/=r;
    L/=r;
    c/=r;
    gcdd(a,L,k1,k2);
    LL ans=c*k1-c*k1/L*L;
    if(L<0)
        L=-L;
    if(ans<0)
        ans+=L;
    printf("%I64d",ans);
    return 0;
}

[POJ 2115] C Looooops

题目描述

A Compiler Mystery: We are given a C-language style for loop of type

for (variable = A; variable != B; variable += C)
  statement;

I.e., a loop which starts by setting variable to value A and while variable is not equal to B, repeats statement followed by increasing the variable by C. We want to know how many times does the statement get executed for particular values of A, B and C, assuming that all arithmetics is calculated in a k-bit unsigned integer type (with values 0 <= x < 2^k) modulo 2^k.

输入

The input consists of several instances. Each instance is described by a single line with four integers A, B, C, k separated by a single space. The integer k (1 <= k <= 32) is the number of bits of the control variable of the loop and A, B, C (0 <= A, B, C < 2^k) are the parameters of the loop.
The input is finished by a line containing four zeros.

输出

The output consists of several lines corresponding to the instances on the input. The i-th line contains either the number of executions of the statement in the i-th instance (a single integer number) or the word FOREVER if the loop does not terminate.

样例数据

样例输入	样例输出
3 3 2 16 3 7 2 16 7 3 2 16 3 4 2 16 0 0 0 0	0 2 32766 FOREVER

解析

用拓展欧几里德方法求出gcd最大公因数，再利用同余性质转化，求同余方程，或者不定方程。其中题目可化为 a+cx=b(mod 2^k) → cx=b-a(mod 2^k)，求最小正整数解。也是求解同余方程。
先将方程化为一般形式：ax=c(mod p) → ax+py=c 。若 gcd(a,p)|c，就可以利用 ax+py=gcd(a,b)(mod p) [一般没有mod p] ，再把变量 x,y 乘上 c/gcd(a,b) 就是答案了。而要求最小正整数解，就是根据 ax+py=gcd(a,p) → a(x+p/gcd(a,p))+p(y-a/gcd(a,p)=gcd(a,p) ，所有的 x' 都满足 x+p/gcd(a,p) 来进行调整，并且取模。因为每对 x 与 x' 都相差 p/gcd(a,p)，那么根据同余的定义，x 和 x' 关于模 p/gcd(a,p) 同余，所以可以一直取模来调整。而对于 p/gcd(a,p) ，为正时取模才有保证最非负的意义。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define  LL  long long
LL gcd(LL a,LL  b,LL &x,LL &y)
{
    if (b==0)
    {
        x=1;
        y=0;
        return a;
    }
    else
    {
        LL r=gcd(b,a%b,x,y);
        LL temp=x;
        x=y;
        y=temp-(a/b)*y;
        return r ;
    }
}

int main()
{
     LL a,b,c,d,k,A,B,C,X,Y;
    while(scanf("%I64d%I64d%I64d%I64d",&a,&b,&c,&k)!=EOF)
    {
        if(!a&&!b&&!c&&!k)
            break;
            C=b-a;
            A=c;
            B=(LL)1<<k;
            d=gcd(A,B,X,Y);
            if(C%d!=0 )
            {
                printf("FOREVER
");
            }
            else
            {
                LL ans=X*C/d;
                LL temp=B/d ;
                ans=(ans%temp+temp)%temp;
                printf("%I64d
",ans);
            }
    }
    return 0 ;
}

[POJ 2142] The Balance

题目描述

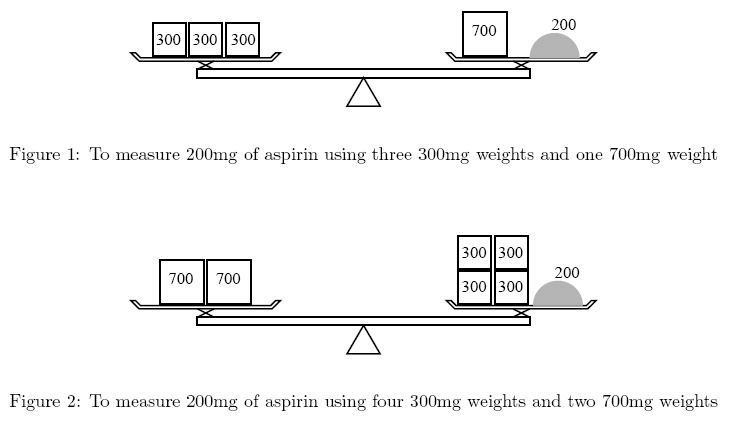
Ms. Iyo Kiffa-Australis has a balance and only two kinds of weights to measure a dose of medicine. For example, to measure 200mg of aspirin using 300mg weights and 700mg weights, she can put one 700mg weight on the side of the medicine and three 300mg weights on the opposite side (Figure 1). Although she could put four 300mg weights on the medicine side and two 700mg weights on the other (Figure 2), she would not choose this solution because it is less convenient to use more weights.
You are asked to help her by calculating how many weights are required.

输入

The input is a sequence of datasets. A dataset is a line containing three positive integers a, b, and d separated by a space. The following relations hold: a != b, a <= 10000, b <= 10000, and d <= 50000. You may assume that it is possible to measure d mg using a combination of a mg and b mg weights. In other words, you need not consider "no solution" cases.
The end of the input is indicated by a line containing three zeros separated by a space. It is not a dataset.

输出

The output should be composed of lines, each corresponding to an input dataset (a, b, d). An output line should contain two nonnegative integers x and y separated by a space. They should satisfy the following three conditions.

You can measure dmg using x many amg weights and y many bmg weights.
The total number of weights (x + y) is the smallest among those pairs of nonnegative integers satisfying the previous condition.
The total mass of weights (ax + by) is the smallest among those pairs of nonnegative integers satisfying the previous two conditions.

No extra characters (e.g. extra spaces) should appear in the output.

样例数据

样例输入	样例输出
700 300 200 500 200 300 500 200 500 275 110 330 275 110 385 648 375 4002 3 1 10000 0 0 0	1 3 1 1 1 0 0 3 1 1 49 74 3333 1

解析

很容易列出方程ax + by = d，很明显应该用扩展欧几里德去求根，求出x、y然后分成两组，求出x可以根据方程推出y，求出y可以根据方程推出x.然后取两组相加的最小值即可。

Code

#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<iostream>

#define LL long long
const int INF=0x3f3f3f3f;

using namespace std;

LL x,y;

LL myabs(LL a)
{
    return a>0?a:-a;
}

LL exgcd(LL a,LL b)
{
    LL t,ans;
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    ans=exgcd(b,a%b);
    t=x;
    x=y;
    y=t-a/b*y;
    return ans;
}

int main()
{
    LL Max,xx,yy,a,b,d,temp,i,flag,aa,bb,t;
    for(;;)
    {
        scanf("%I64d%I64d%I64d",&a,&b,&d);
        if(a==0&&b==0&&d==0)
            break;
        flag=0;
        if(a<b)
        {
            temp=a;
            a=b;
            b=temp;
            flag=1;
        }
        temp=exgcd(a,b);
        x=x*d/temp;
        y=y*d/temp;
        Max=INF;
        t=y*temp/a;
        for(i=t-1;i<=t+1;i++)
        {
            xx=myabs(x+b/temp*i);
            yy=myabs(y-a/temp*i);
            if(xx+yy<Max)
            {
                Max=xx+yy;
                aa=xx;
                bb=yy;
            }
        }
        if(flag)
            printf("%I64d %I64d
",bb,aa);
        else
            printf("%I64d %I64d
",aa,bb);
    }
    return 0;
}

[HDU 4828] Grids

题目描述

度度熊最近很喜欢玩游戏。这一天他在纸上画了一个2行N列的长方形格子。他想把1到2N这些数依次放进去，但是为了使格子看起来优美，他想找到使每行每列都递增的方案。不过画了很久，他发现方案数实在是太多了。度度熊想知道，有多少种放数字的方法能满足上面的条件？

输入

第一行为数据组数T(1<=T<=100000)。
然后T行，每行为一个数N(1<=N<=1000000)表示长方形的大小。

输出

对于每组数据，输出符合题意的方案数。由于数字可能非常大，你只需要把最后的结果对1000000007取模即可。

样例数据

样例输入

样例输出

Case #1:

Case #2:

解析

可以转化为卡特兰数，先把前n个人标为0，后n个人标为1，然后去全排列，全排列的数列，如果每个1的前面对应的0大于等于1，那么就是满足的序列，如果把0看成入栈，1看成出栈，那么就等价于n个元素入栈出栈，求符合条件的出栈序列，这个就是卡特兰数了。然后去递推一下解，过程中需要求逆元去计算。

Code

#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int mod=1000000007;
long long C[1000005];
long long spow(long long x,int n)
{
    if(n==1)
        return x;
    else
    {
        long long v=spow(x, n/2);
        if (n%2==0)
            return v*v%mod;
        else
            return v*v%mod*x%mod;
    }
}
int main()
{
    C[1]=1;
    for(int i=2;i<1000001;i++)
    {
        C[i]=C[i-1]*(4*i-2)%mod;
        C[i]=C[i]*spow(i+1,1000000005)%mod;
    }
    int n,m;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>m;
        cout<<"Case #"<<i<<":"<<endl;
        cout<<C[m]<<endl;
    }
    return 0;
}

[HDU 1930] And Now, a Remainder from Our Sponsor

题目描述

IBM has decided that all messages sent to and from teams competing in the ACM programming contest should be encoded. They have decided that instead of sending the letters of a message, they will transmit their remainders relative to some secret keys which are four, two-digit integers that are pairwise relatively prime. For example, consider the message "THE CAT IN THE HAT". The letters of this message are first converted into numeric equivalents, where A=01, B=02, ..., Z=26 and a blank=27. Each group of 3 letters is then combined to create a 6 digit number. (If the last group does not contain 3 letters it is padded on the right with blanks and then transformed into a 6 digit number.) For example
THE CAT IN THE HAT → 200805 270301 202709 142720 080527 080120
Each six-digit integer is then encoded by replacing it with the remainders modulo the secret keys as follows: Each remainder should be padded with leading 0’s, if necessary, to make it two digits long. After this, the remainders are concatenated together and then any leading 0’s are removed. For example, if the secret keys are 34, 81, 65, and 43, then the first integer 200805 would have remainders 1, 6, 20 and 38. Following the rules above, these combine to get the encoding 1062038. The entire sample message above would be encoded as
1062038 1043103 1473907 22794503 15135731 16114011

输入

The input consists of multiple test cases. The first line of input consists of a single positive integer n indicating the number of test cases. The next 2n lines of the input consist of the test cases. The first line of each test case contains a positive integer (< 50) giving the number of groups in the encoded message. The second line of each test case consists of the four keys followed by the encoded message.
Each message group is separated with a space.

输出

For each test case write the decoded message. You should not print any trailing blanks.

样例数据

样例输入	样例输出
2 6 34 81 65 43 1062038 1043103 1473907 22794503 15135731 16114011 3 20 31 53 39 5184133 14080210 7090922	THE CAT IN THE HAT THE END

解析

中国剩余定理可直接解决。

由于题目中将直接代表字母的二位数字通过求余取模转换为了密文，我们由此发现这恰好可以用中国剩余定理来求解模线性方程组，借此求出取模前的“明文序列”，再转换为字母，得到答案。

<中国剩余定理>

中国剩余定理正是用来求解模线性方程组的。
对于n1，因为它与(n2*n3……*nk)互质，我们可以找到一个系数z1，使得z1*(n2*n3*……nk)%n1=1。设z1*(n2*n3*……*nk)为c1。
同理，对于每个nk，都可以找到一个zi，使得zi*(n1*n2*……*nj |j!=i)%ni=1，设zi*(n1*n2*……*nj |j!=i)为ci x=b1*c1+b2*c2+……bk*ck+m(n1*n2*…*nk) 其中m为任意整数。
x为一组解。(好吧，如果实在不能完全理解，还是建议背一下模板)

#include<cstdio>

#define ll long long

//扩展欧几里得算法 
void exgcd(ll a,ll b,ll &d,ll &x,ll &y)
{
    if(b==0)
　　{
        d=a;
        x=1,y=0;
    }
    else
　　{
        exgcd(b,a%b,d,y,x);
        y-=(a/b)*x;
    }
}

//中国剩余定理 
ll China(int n,ll *m,ll *a)
{
    ll M=1,d,y,x=0;
    for(int i=0;i<n;i++) 
        M*=m[i];
    for(int i=0;i<n;i++)
    {
        ll w=M/m[i];
        exgcd(m[i],w,d,d,y);
        x=(x+y*w*a[i])%M;
    }
    return (x+M)%M;
}

ll m[15],a[15];

int main()
{
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
        scanf("%I64d%I64d",&m[i],&a[i]);
    printf("%lld",China(n,m,a));
    return 0;
}

Code

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<cstring>

#define N 2005

using namespace std;

int key[N],num,n;
int str[N];
int res[N];
int r[N];

void input()
{
    int i;
    scanf("%d",&n);
    memset(res,0,sizeof(res));
    memset(str,0,sizeof(str));
    memset(r,0,sizeof(r));
    memset(key,0,sizeof(key));
    num=0;
    for(i=0;i<4;i++)
        scanf("%d",&key[i]);
    for(i=0;i<n;i++)
        scanf("%d",&str[i]);
}

void exGcd(int a,int b,int &d,int &x,int &y)
{
    if(b==0)
    {
        d=a;
        x=1;
        y=0 ;
        return;
    }
    exGcd(b,a%b,d,x,y);
    int tmp=x;
    x=y;
    y=tmp-(a/b)*y;
}

void getNum()
{
    int a,b,c,d,x,y;
    for (int i=0;i<n;i++)
    {
        r[3]=str[i]%100;
        r[2]=(str[i]%10000)/100;
        r[1]=(str[i]%1000000)/10000;
        r[0]=str[i]/1000000;
        int ta=key[0];
        int tr=r[0];
        for(int j=1;j<4;j++)
        {
            a=ta,b=key[j];
            c=r[j]-tr;
            exGcd(a,b,d,x,y);
            int t=b/d;
            x=(x*(c/d)%t+t)%t;
            tr=ta*x+tr;
            ta=ta*(key[j]/d);
        }
        res[i]=tr;
    }
}

void output ()
{
    int i;
    int a,b,c;
    char destr[10005];
    int len=0;
    for (i=0;i<n;i++)
    {
        a=res[i]/10000;
        b=(res[i]%10000)/100;
        c=res[i]%100;
        if(a!=27)
            destr[len++]='A'+a-1;
        else destr[len++]=' ';
        if(b!=27)
            destr[len++]='A'+b-1;
        else destr[len ++]=' ';
        if(c!=27)
            destr[len++]='A'+c-1;
        else destr[len++]=' ';
    }
    while(destr[len-1]==' ')
    {
        len--;
    }
    for(i=0;i<len;i++)
        printf("%c",destr[i]);
    printf("
");
}

int main ()
{
    int tcase;
    scanf("%d",&tcase);
    while(tcase--)
    {
        input();
        getNum();
        output();
    }
    return 0;
}

Time: 2017-07-06