【SinGuLaRiTy-1013】 Copyright (c) SinGuLaRiTy 2017. All Rights Reserved.
这是 三道 USACO 的题......
第一题:奶牛飞盘
题目描述
有n(2<=n<=20)头奶牛在玩飞盘,可是飞盘飞到了高处。现在他们要想办法叠在一起,去取飞盘。飞盘的高度为H(1 <= H <= 1,000,000,000)。给出每头奶牛的重量、高度、强壮度(能够承受的重量),问他们是否够得到,如果能够取到,求它们额外还能承受最多多少重量。(要保证每头奶牛所承受的重量都不超过它的强壮度)。
输入
第一行包含N和H。
接下来N行,每行三个数,分别表示它的高度、重量和强壮度。所有的数都为正整数。
输出
如果奶牛的队伍可以够到飞盘,输出还能承受的最大额外重量;否则输出“Mark is too tall”.
样例数据
| 样例输入 | 样例输出 |
|
4 10 9 4 1 3 3 5 5 5 10 4 4 5 |
2 |
样例解释
选择:(1)3 3 5 (2)4 4 5 (3)5 5 10
STD Code
#include<cstring> #include<cstdio> #include<cstdlib> #include<iostream> #include<algorithm> #include<cmath> #define INF 20+5 #define MAXN 0x3f3f3f3f using namespace std; struct node { long long int w; long long int s; long long int h; long long int infor; }; node cow[INF]; long long int tot_height=0; long long int height,num; bool cmp(node a,node b) { return a.infor>b.infor; } long long minn=MAXN,ans=-1; bool visited[30]; long long int min(long long int a,long long int b) { if(a<b) return a; else return b; } void dfs(int i,int now_height) { int j; if(now_height>=height) { minn=MAXN; for(int ii=0;ii<num;ii++) if(visited[ii]) minn=min(minn-cow[ii].w,cow[ii].s); if(minn>ans) ans=minn; return ; } else for(j=i;j<num;j++) { visited[j]=1; dfs(j+1,now_height+cow[j].h); visited[j]=0; } } int main() { int tot_weight=0; scanf("%I64d%I64d",&num,&height); for(int i=0;i<num;i++) { scanf("%I64d%I64d%I64d",&cow[i].h,&cow[i].w,&cow[i].s); tot_weight+=cow[i].w; } for(int i=0;i<num;i++) cow[i].infor=cow[i].s-(tot_weight-cow[i].w); sort(cow,cow+num,cmp); dfs(0,0); if(ans==-1) printf("Mark is too tall "); else printf("%lld ",ans); return 0; }
题目分析
看到题目,首先想到的当然是DP或者是贪心。尝试写出DP方程式的时候,猛然发现似乎写不出个所以然来,DP无法同时保证高度最优与重量(也就是强壮度的分配)最优。于是果断放弃DP,尝试贪心。看看样例,似乎发现了一点线索:这似乎就是对于强壮度贪心嘛,水题呀!再看看题目,怎么觉得这样例有点水......这明显不是正解好不好?
我们来看看下面这组数据:
5 10
10 20 5
4 4 6
3 3 5
3 1 7
2 1 8
如果我们以强壮度为贪心策略,那么就会优先选后四头牛,而显然的,只选第一头牛就是最优解。也就是说,若一头牛很重,强壮度很小,高度却很高,在此种思路中就会WA。同理可证明按高度排序是行不通的。
那么,我们就要思考一下复杂一点的贪心了。出于偶然,我想到了在描述奶牛的结构体中定义一个值infor=cow.strong+cow.weight,越想越觉得这个猜想靠谱(其实这个就是正解,具体证法见后),但接下来我就犯了一个致命的错误:用一层for循环把奶牛一个个按排好的顺序叠上去——最后就WA了(看来样例与我自己的样例还是比较水qwq)正确的解法是:由于不是每一头奶牛都可以被选中,即每一头奶牛都有“被选中”与“未选中”两种情况,对于这种线性查找最优解的问题,我们可以进行DFS,不断更新ans,最后得到答案(若到最后都没更新到ans,就说明无解)。
<对于infor=cow.strong+cow.weight贪心策略的证明-反证法>
首先我们来想象一下:面前有一叠牛,infor最大的在最底下,越往上,牛的infor越小。我们对这叠牛从下往上编号123。下面,就是重头戏了:
我们看到第i头牛和第i-1头牛(也就是说cow[i]在cow[i-1]的上面):其中,设第i头牛还能承受的重量为cow[i].strong-W,第i-1头牛还能承受的重量为cow[i-1].strong-(cow[i].weight+W),这两个值的min就是该范围内的答案了;
现在,我们来“扭转乾坤”,把第i头牛和第i-1头牛对调一下位置(现在,cow[i-1]在cow[i]的上面):此时,cow[i-1]还能承受的重量为cow[i-1].strong-W,而cow[i]还能承受的重量为cow[i].strong-(cow[i-1].weight+W),同样的,这两个值取min也是当前范围内的答案。
由于有“infor最大的在最底下,越往上,牛的infor越小”这一条件,即cow[i].strong+cow[i].weight<cow[i-1].strong+cow[i-1].weight,我们可以发现在调换前的min一定比调换后的min更优。以此类推,就可证出该结论。
第二题:马拉松比赛
题目描述
奶牛贝西给他的小伙伴设计了一条马拉松比赛的线路。这条线路上一共有n(n<=100000)个点,它们分布在一个平面坐标系中。它的小伙伴毅力不够,所以不能跑完全程,于是贝西给他们安排了一条子线路(它是一段连续的点,比如设定子线路为【i,j】,表示奶牛需要从点i开始,经过点i+1,点i+2,……,最后到点j)。即使这样,奶牛们仍然可能跳过中间某个点以节省路程,当然这个点不能是子线路的起点或终点。现在,有Q(Q<100000)个操作:操作分为两种,第一种为”U I X Y”,表示将点I的位置设在坐标(X,Y)处;第二种为Q I J,表示设定子线路为点i到点j,需要查询奶牛们从i跑到j的最短路程。(路程是以曼哈顿距离计算的)他们可以跳过中间某个点。
所有的坐标值x,y均在[-1000,+1000]区间。
输入
第一行包含N和Q。接下来N行,每行两个数(X,Y),表示每个点的坐标,按照编号从小到大的顺序给出。
接下来Q行,每行表示一个操作。操作如上所述。
输出
对于每一次查询,输出一个整数,表示该子线路的最短路程(曼哈顿距离)。
样例数据
| 样例输入 | 样例输出 |
|
5 5 -4 4 -5 -3 -1 5 -3 4 0 5 Q 1 5 U 4 0 1 U 4 -1 1 Q 2 4 Q 1 4 |
11 8 8 |
STD Code
#include<cstring> #include<cstdlib> #include<cstdio> #include<cmath> #include<algorithm> #include<iostream> #define MAXN 100010 #define INF 0x3f3f3f3f #define get_mid (tree[root].l+tree[root].r)/2 using namespace std; char ask[5]; int num_point,num_ask; struct node { int X; int Y; }; node point[MAXN]; int Max(int a,int b) { return (a>b ? a : b); } //Distance Function int Abs(int target) { if(target>0) return target; return (-(target)); } int Manhattan(int a,int b) { return Abs(point[a].X-point[b].X)+Abs(point[a].Y-point[b].Y); } //Segment Tree Function struct segment { int l; int r; int sum; int dis; }; segment tree[3*MAXN]; void update(int root) { int mid=get_mid; tree[root].dis=Max(tree[root*2].dis,tree[root*2+1].dis); tree[root].sum=tree[root*2].sum+tree[root*2+1].sum+Manhattan(mid,mid+1); } void change(int root,int pos) { if(tree[root].l==tree[root].r) { if(1<tree[root].l&&tree[root].r<num_point) tree[root].dis=Manhattan(pos-1,pos)+Manhattan(pos,pos+1)-Manhattan(pos-1,pos+1); return; } int mid=get_mid; if(pos<=mid) change(root*2,pos); else change(root*2+1,pos); update(root); } void build(int root,int l,int r) { tree[root].l=l; tree[root].r=r; tree[root].sum=0; tree[root].dis=-INF; if(l==r) return; int mid=(l+r)/2; build(root*2,l,mid); build(root*2+1,mid+1,r); } //Ans Calculation int get_sum(int root,int l,int r) { if(r<tree[root].l||tree[root].r<l) return 0; if(l<=tree[root].l&&tree[root].r<=r) return tree[root].sum; int mid=get_mid; int addition=0; if(l<=mid&&mid<r) addition=Manhattan(mid,mid+1); return get_sum(root*2,l,r)+get_sum(root*2+1,l,r)+addition; } int get_dis(int root,int l,int r) { if(r<tree[root].l||tree[root].r<l) return 0; if(l<=tree[root].l&&tree[root].r<=r) return tree[root].dis; return max(get_dis(root*2,l,r),get_dis(root*2+1,l,r)); } //Main Function int main() { scanf("%d%d",&num_point,&num_ask); build(1,1,num_point); for(int i=1;i<=num_point;i++) { scanf("%d%d",&point[i].X,&point[i].Y); change(1,i); if(i>1) change(1,i-1); if(i<num_point) change(1,i+1); } for(int i=1;i<=num_ask;i++) { scanf("%s",ask); if(ask[0]=='U') { int I,new_X,new_Y; scanf("%d%d%d",&I,&new_X,&new_Y); point[I].X=new_X; point[I].Y=new_Y; change(1,I); if(I>1) change(1,I-1); if(I<num_point) change(1,I+1); } else { int Start,End; scanf("%d%d",&Start,&End); int Sum_ans,Dis_ans=0; Sum_ans=get_sum(1,Start,End); if(End-Start>1) Dis_ans=get_dis(1,Start+1,End-1); printf("%d ",Sum_ans-Dis_ans); } } return 0; }
题目分析
表示考试的时候碰都没有碰——看到这个神奇的题目还有查询操作就感到头大。上网搜过了原题,发现原题实际上并没有U操作与Q操作,因此原题的解法就是一个DP。不过,对于这道经过改动的题来说,显然不是DP就能解决的了:O(n)的DP套上O(n)的查询,总时间复杂度初步估计至少为O(n^2),对于这100000的数据就只有“嘿嘿嘿”。
在看正解之前,先来科普一下:什么是“曼哈顿距离”,我们用一个式子来表示(设一平面上有两点:A(X1,Y1),B(X2,Y2)):Manhattan(A,B)=|X1-X2|+|Y1-Y2|。
下面,我们来看一看正解:我们先忽略掉所谓的“跳过某一个点”的情况,也就是说,先考虑走完所有点的曼哈顿距离,由于点是按路线的顺序给出的,我们很容易得到总路程的表达式(M表示Manhattan距离):
Distance_All=M(A1,A2)+M(A2,A3)+M(A3,A4)+......+M(An-2,An-1)+M(An-1,An)
接着,我们再假设要跳过第k (1<k<n) 个点,那么:
Distance_Skip(k)=M(A1,A2)+M(A2,A3)+M(A3,A4)+......+M(Ak-2,Ak-1)+M(Ak-1,Ak+1)+M(Ak+1,Ak+2)+......+M(An-2,An-1)+M(An-1,An)
我们将Distance_All与Distance_Skip(k)作差,就可以得到跳过第k个点时奶牛们少走的距离(暂且将其称为Benifit(k))了。由于要求最短距离,那么题目就转化为了求所给出区间当中Benifit(k)的最大值。到了这里,我们发现,线段树就可以解决这个问题嘛:建立一个线段树来存储Benifit(k),每次查找就查找该区间的最大值就行了。然而,在写代码的时候你会发现,由于有加点的操作,而且Ans=Distance_Origin-max(Benifit(k)),其中求Distance_Origin要用前缀和来求,所以,我们还需要建立一个线段树来存储从A[Start]到A[End]原本应走的路程(你也可以把一个线段树的结构体开大一点,将Distance_Origin与Benifit的值存到一起)。这样写下来,就没毛病了。
第三题:奶牛慢跑
题目描述
有n(n<=100000)头奶牛在一个无穷长的小道上慢跑。每头奶牛的起点不同,速度也不同。小道可以被分成多条跑到。奶牛只能在属于自己的跑道上慢跑,不允许更换跑道,也不允许改变速度。如果要慢跑t(t<=1000000000)分钟,要保证在任何时候不会有同一跑道上的奶牛相遇,请问最少需要多少条跑道。奶牛开始在哪条跑道是可以随意设置的。
输入
第一行两个整数n,t。
接下来的n行,每行包含两个整数,表示奶牛的位置和速度。位置是非负整数,速度是正整数。所有的奶牛的起点都不相同,按起点递增的顺序给出。
输出
最少的跑道数。
样例数据
| 样例输入 | 样例输出 |
|
5 3 0 1 1 2 2 3 3 2 6 1 |
3 |
STD Code
#include<cstring> #include<cstdio> #include<cmath> #include<algorithm> #include<cstdlib> #include<iostream> typedef long long LL; #define INF 100010 using namespace std; struct node { LL start; LL speed; LL range; int th; }; node cow[INF]; int data[INF]; int f[INF]; int ans; int p=1; int pa[INF]; bool cmp_start(node a,node b) { return a.start<b.start; } bool cmp_range(node a,node b) { if(a.range==b.range) return a.th>b.th; return a.range<b.range; } int tmp[INF],cnt=0; int maxval[INF]; int lowbit(int x){return x&-x;} void add(int x,int val,int num) { while(x<=num){ maxval[x]=max(maxval[x],val); x+=lowbit(x); } } int query(int x) { int rn=0; while(x) { rn=max(rn,maxval[x]); x-=lowbit(x); } return rn; } int main() { int num,t; scanf("%d%d",&num,&t); for(int i=1;i<=num;i++) { scanf("%I64d%I64d",&cow[i].start,&cow[i].speed); cow[i].range=cow[i].start+cow[i].speed*t; } sort(cow+1,cow+num+1,cmp_start); for(int i=1;i<=num;i++) cow[i].th=i; sort(cow+1,cow+num+1,cmp_range); for(int i=1;i<=num;i++) data[i]=num-cow[i].th+1; int ans=0; for(int i=1;i<=num;++i) { t=query(data[i])+1; ans=max(ans,t); add(data[i],t,num); } printf("%d ",ans); return 0; }
题目分析
考试的时候,只写到了按起点位置排序就写不下去了(其实,最开始我还以为这是一道“纯数学水题”——当然,现在也觉得这道题的思维难度确实不大)
下面,我们来画一个图:

通过观察图片我们可以发现:当奶牛A的起点(cow[A].start)小于奶牛B的起点(cow[B].start),且奶牛A的终点(cow[A].range)大于奶牛B的终点(cow[B].range)时,就判定为A在t时间内会追上B,即需要一条新的跑道。由于题目条件中有:“按起点递增的顺序给出”,因此我们不需要排序就可以发现:对于cow[i]来说,只要cow[i].range<cow[k].range (k>i),就说明cow[i]与cow[k]可以共用一条跑道。由此推广:在所有的cow.range中只要属于一个上升子序列,就可以共用一条跑道。这时想到了什么?拦截导弹!也就是说,这时的最长下降子序列的长度就是需要跑道的数量。
不过,问题来了:目前我们所学的求最长下降子序列的时间复杂度是O(n^2)的,对于100000的数据肯定会超时,这时,我们就要用到另一种更优秀的算法了。
在上面的代码中,我用的是线段树(当然,树状数组也是可以的);而网上有一种更为“高级”的【lower_bound解法】,可以上网去搜索自学一下。下面,我来讲讲我的思路:
我们设置一个数组来分别存储数组中以每个数为结尾的最长上升子序列(若有多个,取结尾最小的),这样一来,就可以通过判断新增的数是否比之前的结尾大,若比之前的结尾大,就可以更新当前最长上升子序列的值。当然,如果直接for循环暴力,时间复杂度还是O(n^2)的,这时,我们就要用线段树或树状数组来进行优化,这样时间复杂度就会变为O(n logn)了。本题中的最长下降子序列也是一样的。
<最长不下降子序列-树状数组解法小结>
不降子序列求的是一个元素的值单调不降的序列。
传统的状态设计便是使用f[n] 表示到达第n位时的最长不降子序列。
那么转移就是:
f[n]=max(f[i]+1)
其中要求:a[i]<=a[n] && i<=n
举个例子:
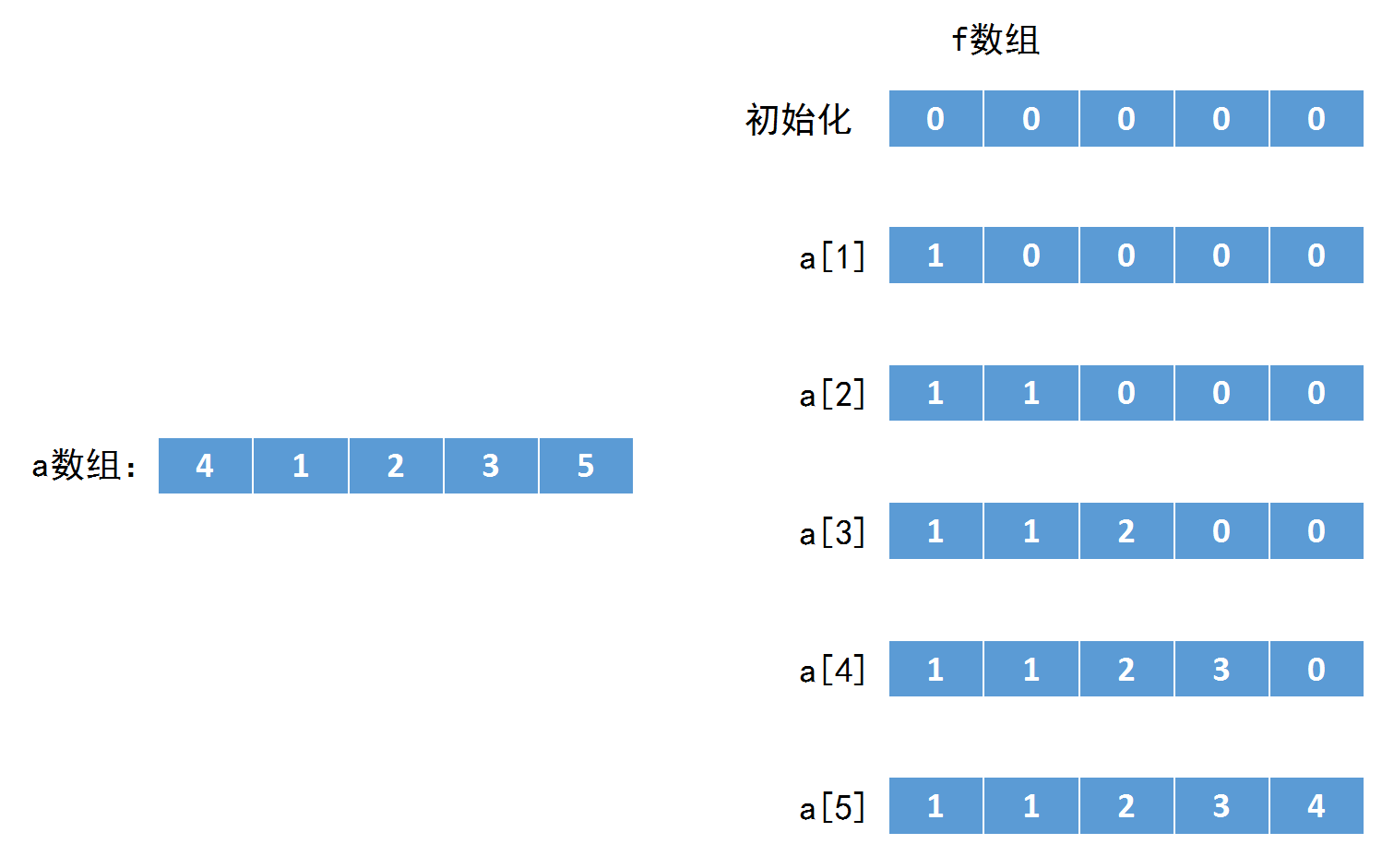
那么想要使得复杂度比较优,就不能通过枚举所有满足条件的i来找到最优解。那么树状数组在其中就可以起到很快的查询到最优的f[i]的作用。
这里的树状数组是当做桶来使用的。我们可以先考虑桶的情况。我们现在开一个桶,其下标 x 表示 a[i]=x 的f[i]的最大值。
T[x]=max(f[i]); //其中a[i]=x
那么需要转移到f[n]的话,就先找到a[n]在桶中的位置,然后查询所有a[n]之前所存储的最大值中的最大值。也就相当于是一段前缀中的最大值。
f[n]=max(T[x]+1); //其中x<=a[n]
在枚举f[n]的同时,也将f[n]的值扔入桶中,方便之后的更新。
T[a[n]]=max(T[a[n]],f[n]);
而桶的前缀和是可以用树状数组来优化的,那么查询一段前缀的最大值和更改某个位置的值就可以在O(n logn)的时间内完成了。
Time : 2017-03-28