题解:[COCI2011-2012#5] BLOKOVI
Description
PDF : https://hsin.hr/coci/archive/2011_2012/contest5_tasks.pdf
题意:
有 (N) 个已知质量的矩形,长都是 2 ,高都是 (h) 。把它们放到一个平面直角坐标系里,满足:
- 各矩形的边与坐标轴平行;
- 各矩形下底边的纵坐标各不相同,分别为 (0,h,2h,dots,(N-1)h) ;
- 最底端的矩形左下角坐标恒为 ((-2,0)) ,右下角为原点 ((0,0)) 。
我们记一个矩形的 (Xcentre) 为其下底边的中点,
一个或多个矩形的 (Xbarycentre) 是这些矩形的 (Xcentre) 的加权平均数,公式为:
其中 (m_i) 是各个矩形的质量。
如果 (N) 的矩形的摆放方案是稳定的,它应当满足对于任意的矩形 (A) ,在 (A) 上方的各矩形的 (X-barycentre) 符合 (|Xbarycentre - Xcentre(A)| leq 1) 。
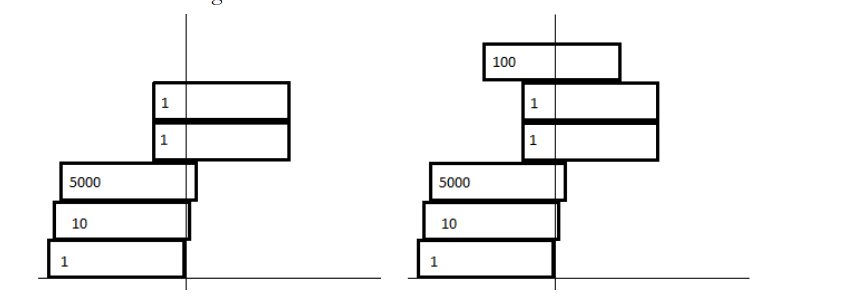
左图的摆放方案就是不稳定的,因为最上方两个矩形的 (Xcentre) 距离落在的下面那个矩形的右侧。
右图的的拜访方案则是稳定的。
现在我们给出从下至上各个矩形的质量,在保证摆放方案稳定的情况下,请你找出所有矩形右下角顶点的横坐标最大值可能是多少。
注意,你不能改变矩形的摆放顺序和第一个矩形的位置。
(2leq N leq 3e5)
至今,我仍然无法用自然流畅的语言翻译英文题面……大家姑且一看,建议还是读原题。
Algorithm
太神了,我只能说不愧是克罗地亚题。
首先, (Nleq3e5) 的规模要求了一个线性的算法,这似乎是比较困难的。
为什么呢?我们自底而上地考虑,考虑放置某个矩形的时候,未来放置的其它矩形很可能会影响它的放置。
换言之,我们需要「回头」。
说到「回头」,我们很容易想到动态规划中「后效性」的概念。
而这道题正是一个 多阶段决策最优化问题 。我们不妨就试着消除后效性,使用动态规划来解决它。
试着消除本题的后效性是一件并不困难的问题。只需要回顾刚刚我们需要「回头」的情形,很容易就能发现:
任何一个矩形的放置方法只可能影响在它之下的矩形放置。
当然上面矩形的绝对坐标也会受到影响,但是相对位置并不会发生变化。
因此,我们当然可以自顶向下地考虑各个矩形的放置,这样就自然可以消除后效性了。
当然,题目还要求最底下的那个矩形的位置固定,因此我们需要将自顶向下考虑得到的相对坐标转化为答案要求的绝对坐标。
既然后效性没了,那么接下来,我们考虑动态规划的状态转移。
我们在这里仍然存在一个小小的问题:
我们是在一个笛卡尔坐标系上放矩形,可以放置的位置可是有不可数无穷多个啊。
直觉敏感的同学或者勇敢莽撞的同学一定发现了:我们只要往最左边或者最右边放就行了。
这点是容易感性地证明的:
考虑不是把某个矩形放在最左或最右的情况,将其与其下的矩形在不改变其相对位置的情况下、整体地左移或右移,一定可以使得答案不变得更劣。
这句话稍稍有点复杂,不过其意涵是比较容易理解的。
每个矩形能放置的极限位置也是容易计算的。我们先计算向右放最远能放多少。
记
由定义又有:
其中,
然后一个带入,
按照上述分析,直接取 (d_k = 1) ,那么放置导致的重心向右偏移量即为 (Large frac{m_k}{sum_{i = k}^n m_i}) 了。
由对称性,向左放最大偏移量即为 (2 - Large frac{m_k}{sum_{i = k}^n m_i}) 。
接下来我们只要顺次考虑某个矩形是放在最左还是最右即可了,这是一个类似 01背包的模型。
代码很简单:
#include<bits/stdc++.h>
using namespace std;
template<class T>
inline void read(T &x)
{
char c = getchar(); x = 0;
while(c < '0' || '9' < c) c = getchar();
while('0' <= c && c <= '9')
{
x = (x << 1) + (x << 3) + c - 48;
c = getchar();
}
}
const int N = 3e5 + 10;
int n, a[N];
int main()
{
read(n);
for(int i = 1; i <= n; read(a[i++]));
double ans = 0, sum = 0;
for(int i = n; i > 1; --i)
{
sum += a[i];
double del = a[i] / sum;
ans = max(ans, max(ans + del, 2 - del));
}
printf("%.8f
", ans);
return 0;
}