平面图 / 平面图判定
题目链接:ybt金牌导航3-6-5 / luogu P3209
题目大意
给你一个图,保证图存在哈密顿路径(即图中存在一个包含所有顶点的环),且给出。
问你它是否是一个平面图。
如果能将一个无向图画在平面上使得每两个无重合顶点的边都不会相交,那这个图就是平面图。
思路
我们看到这个东西似乎没有思路,考虑把样例的两个图搞出来:
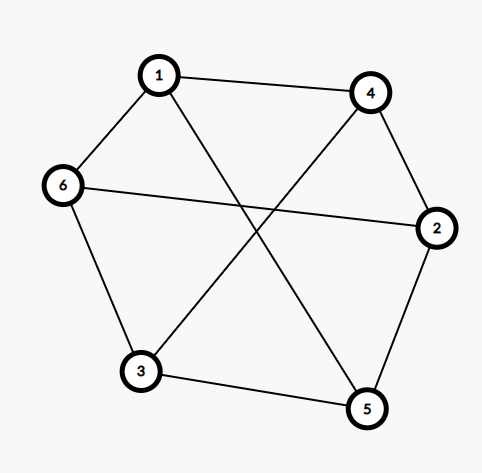
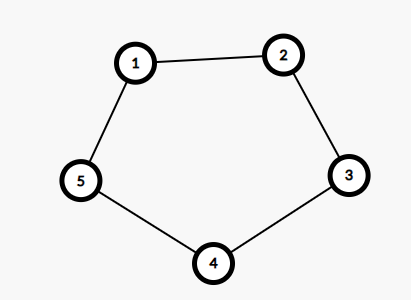
第二个可以这非常明显,但为什么第一个不行呢?
你会发现把哈密顿路径的边去掉,里面的边无论怎么搞都会交在一起。
那你就会想你是不是判断一下里面的会不会交在一起就可以了。
至于怎么判断,我们可以先按哈密顿路径把点重新编号。
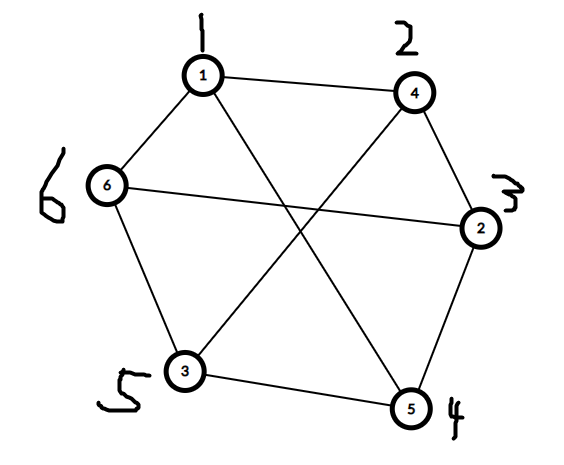
那考虑到如果两条边 ((a,b)) 和 ((c,d)) 有交点,那它们会满足这样的关系:(a<c<b<d)
简称把环搞成一条链之后着两条边有重合的部分。(当然 (c<a<d<b) 也行)
但是你以为这样就结束了?
我们把原来不行的样例中 ((3,4)) 这条边去掉。
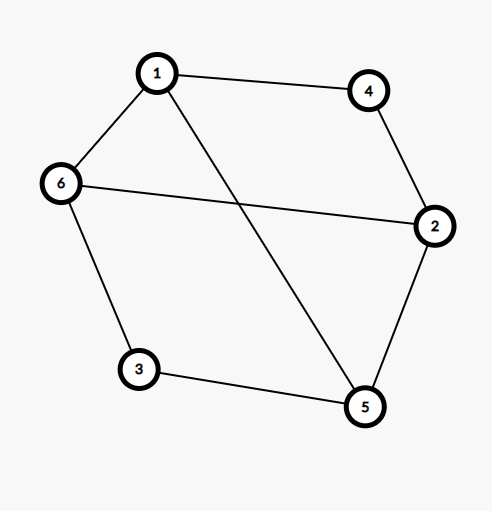
你以为它不行,但它其实可以这样:
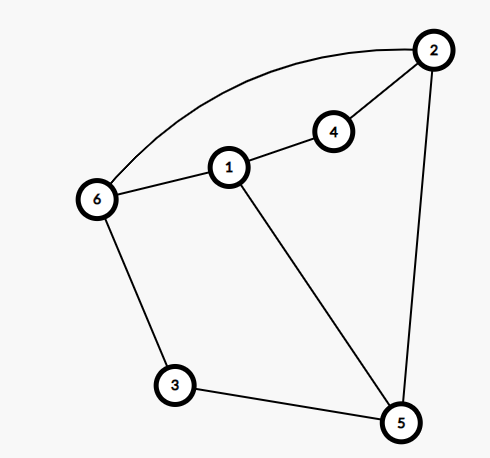
什么意思呢?就是它连不是哈密顿的边的时候不一定要连在环的里面,它是可以在外面连的!
那就相当于对于一条不在哈密顿路径上的边,它可以在里面连,也可以在外面连,那原来的相交关系只要用这两个边一个里面一个外面就不会影响。
那也就说如果两个边之间有矛盾关系,那一个选了里面另一个就一定要外面,一个选了外面另一个就一定要在里面。
然后你发现它就是 2-sat。
但是你会发现你不是哈密顿距离上的边太多了,大概是 (10^4) 级别,你两两之间判断是否相交就炸了啊。
这时候就要用到平面图的性质了。
要用到的性质是如果一个图是平面图,点的个数是 (n),边的个数是 (m),则一定满足 (mleq3 imes n-6)。
关于这里的证明就不多讲了,可以去看看一个 PPT。
图论4-6 平面图
(当然你上网直接搜也应该搜得到)
然后你就直接判断,如果 (m>3 imes n-6) 就直接是 NO。
那你的 (m) 就变成了 (10^2sim10^3) 级别的,就可以 (m^2) 搞了。
代码
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
struct node {
int to, nxt;
}e[5000001];
int T, n, m, x, y, dy[10001];
int v[10001], lx[10001], ly[10001];
int le[10001], KK, low[10001], dfn[10001];
int tmp, tot, sta[10001], in[10001];
bool a[501][501], yes;
void csh() {
memset(a, 0, sizeof(a));
KK = 0;
memset(le, 0, sizeof(le));
memset(dfn, 0, sizeof(dfn));
tmp = 0;
tot = 0;
memset(in, 0, sizeof(in));
}
void add(int x, int y) {
e[++KK] = (node){y, le[x]}; le[x] = KK;
}
void tarjan(int now) {
dfn[now] = low[now] = ++tmp;
sta[++sta[0]] = now;
for (int i = le[now]; i; i = e[i].nxt)
if (!dfn[e[i].to]) {
tarjan(e[i].to);
low[now] = min(low[now], low[e[i].to]);
}
else if (!in[e[i].to]) low[now] = min(low[now], low[e[i].to]);
if (dfn[now] == low[now]) {
in[now] = ++tot;
while (sta[sta[0]] != now) {
in[sta[sta[0]]] = tot;
sta[0]--;
}
sta[0]--;
}
}
int main() {
scanf("%d", &T);
while (T--) {
csh();
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d %d", &x, &y);
a[x][y] = 1;
a[y][x] = 1;
}
for (int i = 1; i <= n; i++) {
scanf("%d", &v[i]);
dy[v[i]] = i;
}
if (n * 3 - 6 < m) {//平面图定理
printf("NO
");
continue;
}
v[n + 1] = v[1];
for (int i = 1; i <= n; i++)
a[v[i]][v[i + 1]] = a[v[i + 1]][v[i]] = 0;
m = 0;//找到不在哈密顿路径上的边
for (int i = 1; i <= n; i++)
for (int j = 1; j < i; j++)
if (a[i][j]) {
m++;
lx[m] = i;
ly[m] = j;
if (dy[lx[m]] > dy[ly[m]]) swap(lx[m], ly[m]);
}
for (int i = 1; i <= m; i++)//判断这些边之间那些会相交(相交就不能同时摆在里面 / 外面)
for (int j = 1; j < i; j++)
if (dy[lx[i]] < dy[lx[j]] && dy[lx[j]] < dy[ly[i]] && dy[ly[i]] < dy[ly[j]]) {
add(i, m + j);
add(j, m + i);
add(m + i, j);
add(m + j, i);
}
else if (dy[lx[j]] < dy[lx[i]] && dy[lx[i]] < dy[ly[j]] && dy[ly[j]] < dy[ly[i]]) {
add(i, m + j);
add(j, m + i);
add(m + i, j);
add(m + j, i);
}
for (int i = 1; i <= m + m; i++)
if (!dfn[i]) tarjan(i);
yes = 1;
for (int i = 1; i <= m; i++)
if (in[i] == in[m + i]) {
yes = 0;
break;
}
if (yes) printf("YES
");
else printf("NO
");
}
return 0;
}