求欧拉函数:小于等于n,和n互质的数的个数
int euler_phi(int n) { int m=int(sqrt(n+0.5)); int ans=n; for (int i=2;i<=m;i++) if (n%i==0) { ans=ans/i*(i-1); while (n%i==0) n/=i; } if (n>1) ans=ans/n*(n-1); return ans; }
筛法求欧拉函数
void phi_table(int n,int* phi) { for (int i=2;i<=n;i++) phi[i]=0; phi[1]=1; for (int i=2;i<=n;i++) if (!phi[i]) for (int j=i;j<=n;j+=i) { if (!phi[j]) phi[j]=j; phi[j]=phi[j]/i*(i-1); } }
求逆元的方法:
应用环境:
当(a/b)%p这个转化为解bx---1modp,所以
求bx%p就可以了,x是b的逆元
求b的逆元怎么办?
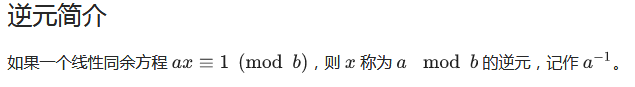
1.扩欧
void ex_gcd(int a,int b,int&x,int&y) { if(b==0) { x=1,y=0; return; } ex_gcd(b,a%b,x,y); int t=x; x=y; y=t-a/b*y; return; }
2.快速幂

#define ll long long inline ll poW(ll a,ll b){ long long ans=1; a%=p; while (b){ if (b&1) ans=((ans*a)%p+p)%p; a=(a*a)%p; b>>=1; } return ans%p; }
3.线性求逆元

inv[i]=(p-p/i)*inv[p%i]%p;
线性同余方程

int ex_gcd(int a,int b,int& x,int& y){//扩欧求逆元 if(b==0){ x=1; y=0; return a; } int d=ex_gcd(b,a%b,x,y); int temp=x;x=y;y=temp-a/b*y; return d; } bool liEu(int a,int b,int c,int&x,int &y){ int d=ex_gcd(a,b,x,y); if(c%d!=0) return 0; int k=c/d; x*=k; y*=k; return 1; }
高斯消元
double gauss() { double ans = 1; for (int i=0; i<n; i++) { int sid = -1; for (int j=i; j<n; j++) if (abs(mat[j][i]) > eps) { sid = j; break; } if (sid == -1) continue; if (sid != i) { for (int j=0; j<n; j++) { swap(mat[sid][j],mat[i][j]); ans = - ans; } } for (int j=i+1; j<n; j++) { double ratio = mat[j][i]/mat[i][i]; for (int k=0; k<n; k++) { mat[j][k] -= mat[i][k] * ratio; } } } for (int i=0; i<n; i++) ans *= mat[i][i]; return abs(ans); } };
卢卡斯定理:
p为质数,C(n, m) % p = C(n / p, m / p) * C(n%p, m%p) % p
对于C(n / p, m / p),如果n / p 还是很大,可以递归下去,一直到世界的尽头
ll lucas(int n, int m) { if(n<m) return 0; ll ans=1; for(; m; n/=P, m/=P) ans = ans*C(n%P, m%P)%P; return ans; }
扩展卢卡斯:
p不是质数时,C(n,m)%p
ll Pow(ll a,ll b,ll P){ ll ans=1; for(;b;b>>=1,a=a*a%P) if(b&1) ans=ans*a%P; return ans; } void exgcd(ll a,ll b,ll &d,ll &x,ll &y){ if(b==0) d=a,x=1,y=0; else exgcd(b,a%b,d,y,x),y-=(a/b)*x; } ll Inv(ll a,ll n){ ll d,x,y; exgcd(a,n,d,x,y); return d==1?(x+n)%n:-1; } ll Fac(ll n,ll p,ll pr){ if(n==0) return 1; ll re=1; for(ll i=2;i<=pr;i++) if(i%p) re=re*i%pr; re=Pow(re,n/pr,pr); ll r=n%pr; for(int i=2;i<=r;i++) if(i%p) re=re*i%pr; return re*Fac(n/p,p,pr)%pr; } ll C(ll n,ll m,ll p,ll pr){ if(n<m) return 0; ll x=Fac(n,p,pr),y=Fac(m,p,pr),z=Fac(n-m,p,pr); ll c=0; for(ll i=n;i;i/=p) c+=i/p; for(ll i=m;i;i/=p) c-=i/p; for(ll i=n-m;i;i/=p) c-=i/p; ll a=x*Inv(y,pr)%pr*Inv(z,pr)%pr*Pow(p,c,pr)%pr; return a*(MOD/pr)%MOD*Inv(MOD/pr,pr)%MOD; } ll Lucas(ll n,ll m){ ll x=MOD,re=0; for(ll i=2;i<=MOD;i++) if(x%i==0){ ll pr=1; while(x%i==0) x/=i,pr*=i; re=(re+C(n,m,i,pr))%MOD; } return re; }
中国剩余定理:

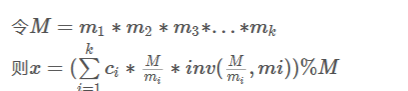
inv是逆元 欧几里得定理求
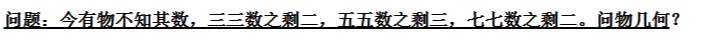

#include<cstdio> #define ll long long //扩展欧几里得算法求逆元 void gcd(ll a,ll b,ll &d,ll &x,ll &y) { if(b==0){ d=a; x=1,y=0; } else{//else不能省略 gcd(b,a%b,d,y,x); y-=(a/b)*x; } } //中国剩余定理 ll China(int n,ll *m,ll *a) { ll M=1,d,y,x=0; for(int i=0;i<n;i++) M*=m[i]; for(int i=0;i<n;i++){ ll w=M/m[i]; gcd(m[i],w,d,d,y); x=(x+y*w*a[i])%M; } return (x+M)%M; } ll m[15],a[15]; int main() { int n; scanf("%d",&n); for(int i=0;i<n;i++) scanf("%lld%lld",&m[i],&a[i]); printf("%lld",China(n,m,a)); }
扩展中国剩余定理:m们不互质了
括号表示最大公约数gcd

LL gcd(LL a, LL b) {//求gcd return b == 0 ? a : gcd(b, a % b); } LL exgcd(LL a, LL b, LL &x, LL &y) {//用扩欧求逆元 if (b == 0) {x = 1, y = 0; return a;} LL r = exgcd(b, a % b, x, y), tmp; tmp = x; x = y; y = tmp - (a / b) * y; return r; } LL inv(LL a, LL b) {//保存他的逆元 LL r = exgcd(a, b, x, y); while (x < 0) x += b; return x; }