其实这道题不用组合数!不用容斥!
只需要一个gcd和无脑找规律(滑稽
乍一看题目,如果单纯求合法三角形的话情况太多太复杂,我们可以从局部入手,最终扩展到整体。
首先考虑这样的情况:
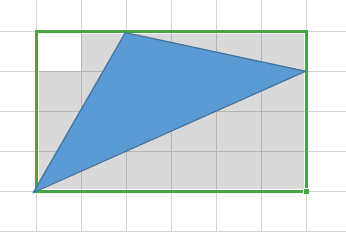
类似地,我们把三角形三个顶点都在网格边界上,且网格内任意一条线都可以把三角形切成两部分的情况,称为完全覆盖。
下面这种就不算:
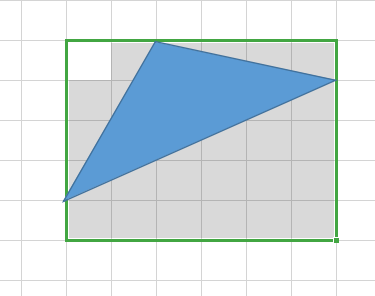
不难发现每个顶点在格点上的三角形,都有且仅有一个被它完全覆盖的网格。
所以可将原问题转化为:求出矩形中所有子矩形的完全覆盖三角形数。
又因为完全覆盖三角形数只与子矩形大小有关,与其位置无关,
而且手模一下可以发现
一个(n*m)的矩形内,大小为(i*j)的子矩形个数为((n-i+1)*(m-j+1))。
所以接下来只要求解一定长宽矩形内 完全覆盖三角形的的个数即可
然后观察可得 (迄今为止我似乎没有用除了观察之外的方法证明过东西)
如果三角形XYZ完全覆盖矩形ABCD,那么它至少有一端点在ABCD的角上。
那么接下来就可以按照 XYZ有几个端点在矩形角上分类讨论。
设矩形长为i,宽为j。
- 一个端点在角上
角的选择有4种,三角形另外两端点必在两边上,共有((i-1)*(j-1))种。
所以这部分答案为(4*(i-1)*(j-1))
- 两个端点在角上
第一种:
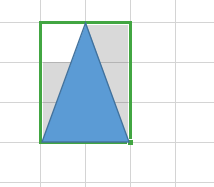
答案:(i-1)
第二种:
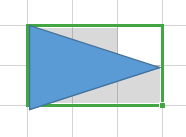
答案:(j-1)
第三种:
三角形有一条边与矩形对角线重合。
此时三角形剩下那个端点除了四个角以及它的对边上的格点之外,可以随便放。
那么这条对边(即矩形的一条对角线)上有几个格点呢?
(gcd(i,j)-1)个。(不包括对边的两个端点)
答案:((i+1)*(j+1)-4-gcd(i,j)+1)
- 三个端点在角上
显然4种。
另外,以上三种情况都可以对称过去得到不同的方案,所以(*2)。
化简可得(ans=6*i*j-2*gcd(i,j))
复杂度:(O(mnlog^{m+n}))
#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
typedef long long ll;
ll m,n;
int gcd(int x,int y)
{
if(!y)return x;
return gcd(y,x%y);
}
int main()
{
scanf("%lld%lld",&m,&n);
ll ans=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
ans+=(6*i*j-2LL*gcd(i,j))*(n-i+1)*(m-j+1);
cout<<ans<<endl;
return 0;
}