前言
话说中国剩余定理好早就会了,但是一直木有接触过拓展的。
只知道它是个什么东东。
最近似乎需要它了,稍微学了学,似乎还挺简单的。
小结一下~
简介
中国剩余定理我们都懂吧?
而拓展则是把它后面的模数变成一个非质数,(当然,各个方程的模数互质)。
然后求出最小的x的解。
做法
似乎拓展之后很难用原来的套路来搞了。
怎么办?
我们发现,我们可以利用一些奇怪的推柿子大法来合并柿子。
考虑合并一下两个柿子:
(x equiv c1 (mod m1))
(x equiv c2 (mod m2))
转化一下:
(x=c1+m1*k1)
(x=c2+m2*k2)
合并、移项
(m1*k1=c2-c1+m2*k2)
设(g=gcd(m1,m2))
柿子两边同除g得:
(frac{m1}g*k1=frac{c2-c1}g+frac{m2}g*k2)
我们考虑转化一下:
(frac{m1}g*k1 equiv frac{c2-c1}g (mod frac{m2}g))
当然,这个时候我们发现,(frac{c2-c1}g)这条柿子一定要是整数,否则就有小数了,判断一下。
于是,现在我们已经去掉了一个k2了,但是左边依然很不优美,接下来考虑化简一波。
设(ny())表示求逆元。
(k1equiv ny(frac{m1}g)*frac{c2-c1}g (mod frac{m2}g))
(k1=ny(frac{m1}g)*frac{c2-c1}g+frac{m2}g*y)
还记得这条柿子吗?
(x=c1+m1*k1)
于是我们把(k1)带回去
(x=c1+ny(frac{m1}g)*frac{c2-c1}g*m1+frac{m2*m1}g*y)
去掉y就变成:
(x equiv c1+ny(frac{m1}g)*frac{c2-c1}g*m1 (mod frac{m2*m1}g))
不就实现了合并吗?
然后逆元求解可以利用我们的拓展欧几里得。
当然要注意的一点是:小心爆longlong,可能需要用到龟速乘。
应用
例题:(最近做的一道)
Comet OJ - Contest #10 鱼跃龙门

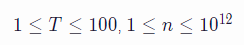
怎么做?
考虑把某个n给分解质因数。
(n=q_1^{p_1}*q_2^{p_2}*……*q_m^{p_m})
考虑m=1的情况:
x只可能是:(y*q_m^{p_m})或是(y*q_m^{p_m}-1)
然后m的个数不可能超过12。
因此,我们考虑直接枚举每种质因子是(y*q_m^{p_m})还是(y*q_m^{p_m}-1)。
然后联立方程式,利用拓展中国剩余定理求解即可。
时间复杂度:(O(2^12*12*log))
然鹅这题比较逗比的是,用这种做法会爆longlong,然后就要打龟速乘。
而时间有很紧,因此要卡卡常。
这也是为什么我比赛T了17次没切的原因QWQ。
#include<bits/stdc++.h>
using namespace std;
int t;
long long zs[1000011],bz[1000011],p[1000011],flag[1000011];
long long n,x,y,gs,mi[21],m[21],c[21],ans;
bool bzz;
long long gcd(long long a,long long b)
{
if (b==0) return a;
else return gcd(b,a%b);
}
long long exgcd(long long a,long long b,long long &x,long long &y)
{
if (b==0)
{
x=1;y=0;return a;
}
else
{
long long d=a/b;
long long c=exgcd(b,a-b*d,x,y);
long long z=x;
x=y;y=z-d*y;
return c;
}
}
long long ny(long long a,long long b)
{
long long z=exgcd(a,b,x,y);
while (x<0)
{
x+=b;
}
return x;
}
long long cheng(long long a,long long b,long long mo)
{
long long t=0;
while(b)
{
t=(t+a*(b&1023))%mo;
b>>=10;
a=a*1024%mo;
}
return t;
}
#define R register
int main()
{
mi[0]=1;
for (int i=1;i<=20;i++)
{
mi[i]=mi[i-1]*2;
}
for (int i=2;i<=1000000;i++)
{
if (bz[i]==0)
{
zs[0]++;
zs[zs[0]]=i;
for (int j=1;j*i<=1000000;j++)
{
bz[j*i]=1;
}
}
}
scanf("%d",&t);
while (t>0)
{
t--;
scanf("%lld",&n);
if (n==1)
{
printf("1
");
continue;
}
long long j=0;
gs=0;
flag[1]=0;
for (int i=1;i<=zs[0];i++)
{
if (n%zs[i]==0)
{
gs++;
p[gs]=1;
if (zs[i]==2)
{
flag[1]=1;
}
}
while (n%zs[i]==0)
{
p[gs]=p[gs]*zs[i];
n=n/zs[i];
}
if (zs[i]>n)
{
break;
}
}
if (n>1)
{
gs++;
p[gs]=n;
}
ans=20000000000000000;
for (int i=1;i<=mi[gs]-1;i++)
{
long long j=i;
memset(m,0,sizeof(m));
memset(c,0,sizeof(c));
int k=1;
while (j>0)
{
if (flag[k]==1)
{
m[k]=p[k]*2;
}
else m[k]=p[k];
if (j%2==1)
{
c[k]=m[k]-1;
}
else c[k]=0;
k++;j=j/2;
}
for (int j=k;j<=gs;j++)
{
if (flag[j]==1)
{
m[j]=p[j]*2;
}
else m[j]=p[j];
c[j]=0;
}
bzz=true;
for (R long long j=2;j<=gs;j++)
{
R long long m1(m[j-1]),m2(m[j])
,c1(c[j-1]),c2(c[j])
,T(gcd(m1,m2))
,mo(m2/T);
if ((c2-c1)%T!=0)
{
bzz=false;break;
}
m[j]=(m1*m2)/T;
R long long op(ny(m1/T,mo)),oq(c2-c1),kk(ny(T,mo));
if (op>1000000000 && oq>1000000000)
c[j]=(cheng(oq,op,mo)*kk)%mo*m1+c1;
else
c[j]=(oq*kk%mo*op)%mo*m1+c1;
c[j]=c[j]%m[j];
if(c[j]<0)c[j]+=m[j];
}
if (bzz==true)
{
ans=min(ans,c[gs]);
}
}
printf("%lld
",ans);
}
}