Games
Competitive environments: in which the agents’ goal are in conflict, giving rise to adversarial search problems.
Games: adversarial search problems. In AI, the most common games are deterministic, fully observable environments in which two agents act alternately and in which the utility values at the end of the game are always equal and opposite.
A game can be formally defined as a kind of search problem with the following elements:
·S0: The initial state, which specifies how the game is set up at the start.
·PLAYER(s): Defines which player has the move in a state.
·ACTIONS(s): Returns the set of legal moves in a state.
·RESULT(s, a): The transition model, which defines the result of a move.
·TERMINAL-TEST(s): A terminal test, which is true when the game is over and false otherwise. States where the game has ended are called terminal states.
·UTILITY(s, p): A utility function(a.k.a. also called an objective function or payoff function), applied to terminal states, defines the final numeric value for a game that ends in terminal state s for a player p. In chess, the outcome is a win, loss or draw, with value +1, 0, or 1/2. Some games have a wider variety of possible outcomes, e.g. In backgammon the payoffs range from 0 to +192.
A zero-sum game is one where the total payoff to all players is the same for every instance of the game. e.g. Chess, 0+1=1+0=1/2+1/2.
Game tree: Defined by the initial state, ACTIONS function and RESULT function, a tree where the nodes are game states and the edges are moves.
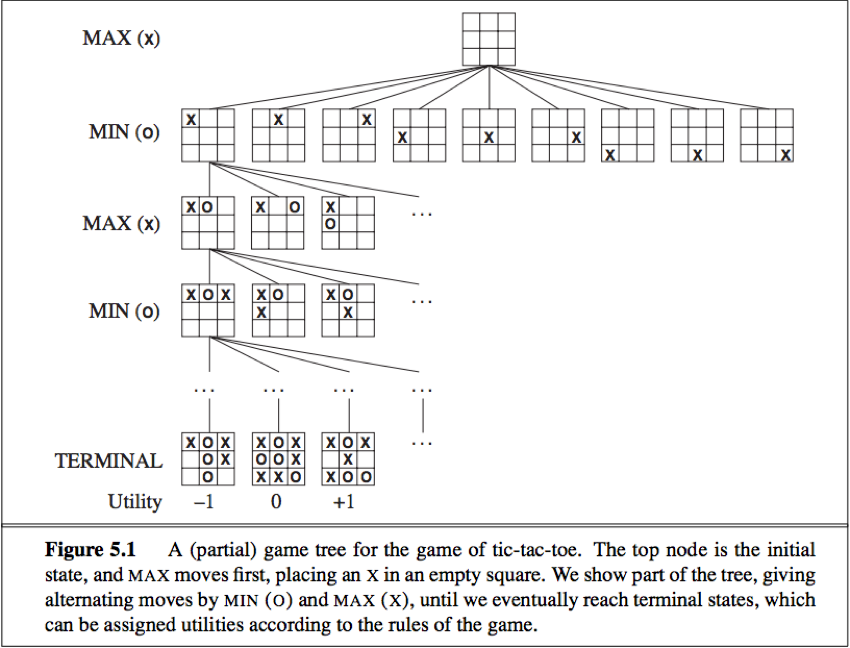
(The utility values on leaf nodes are from the point of view of MAX)
Search tree: A tree that is superimposed on the full game tree, and examines enough nodes to allow a player to determine what move to make.
Optimal decisions in games
Optimal solution: In adversarial search, the optimal solution is a contingent strategy, which specifies MAX(the player on our side)’s move in the initial state, then MAX’s move in the states resulting from every possible response by MIN(the opponent), then MAX’s moves in the states resulting from every possible response by MIN to those moves, and so on.
One move deep: If a particular game ends after one move each by MAX and MIN, we say that this tree is one move deep, consisting of two half-moves, each of which is called a ply.
Minimax value: The minimax value of a node is the utility (for MAX) of being in the corresponding state, assuming that both players play optimally from there to the end of the game. The minimax value of a terminal state is just its utility.
Given a game tree, the optimal strategy can be determined from the minimax value of each node, i.e. MINIMAX(n).
MAX prefers to move to a state of maximum value, whereas MIN prefers a state of minimum value.
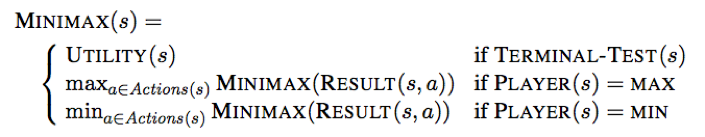
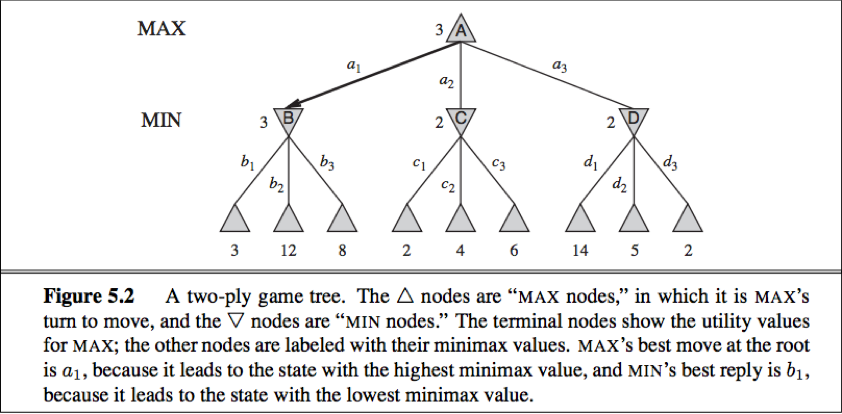
The minimax algorithm
The minimax algorithm computes the minimax decision from the current state. The recursion proceeds all the way down to the leaves of the tree, and then the minimax value are backed up through the tree as the recursion unwinds.

Time complexity: O(b^m)
Space complexity: O(bm) if generate all actions at once, O(m) if generate actions one at a time
The maximum depth of the tree is m and there are b legal moves at each time.
In two-player zero-sum games with perfect information, the minimax algorithm can select optimal moves by a depth-first enumeration of the game tree.
Multiplayer games
We need to replace the single value for each node with a vector of values. E.g. a vector <VA, VB, VC> is associated with each node in a three-player game with players A, B, and C.
For terminal states, this vector gives the utility of the state from each player’s viewpoint.
For nonterminal states, the backed-up value of a node n is always the utility vector of the successor state with the highest value for the player choosing at n.
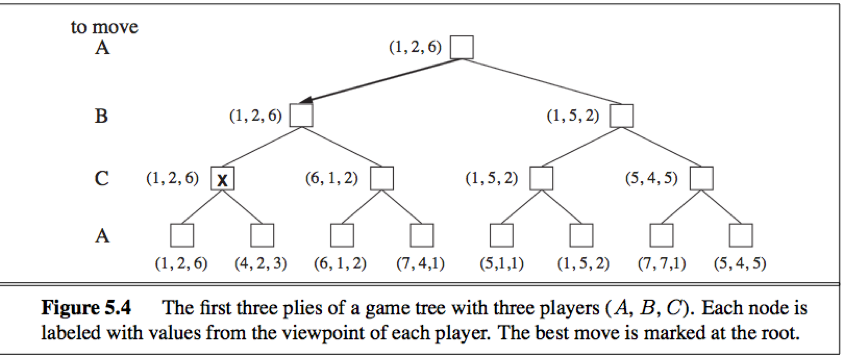
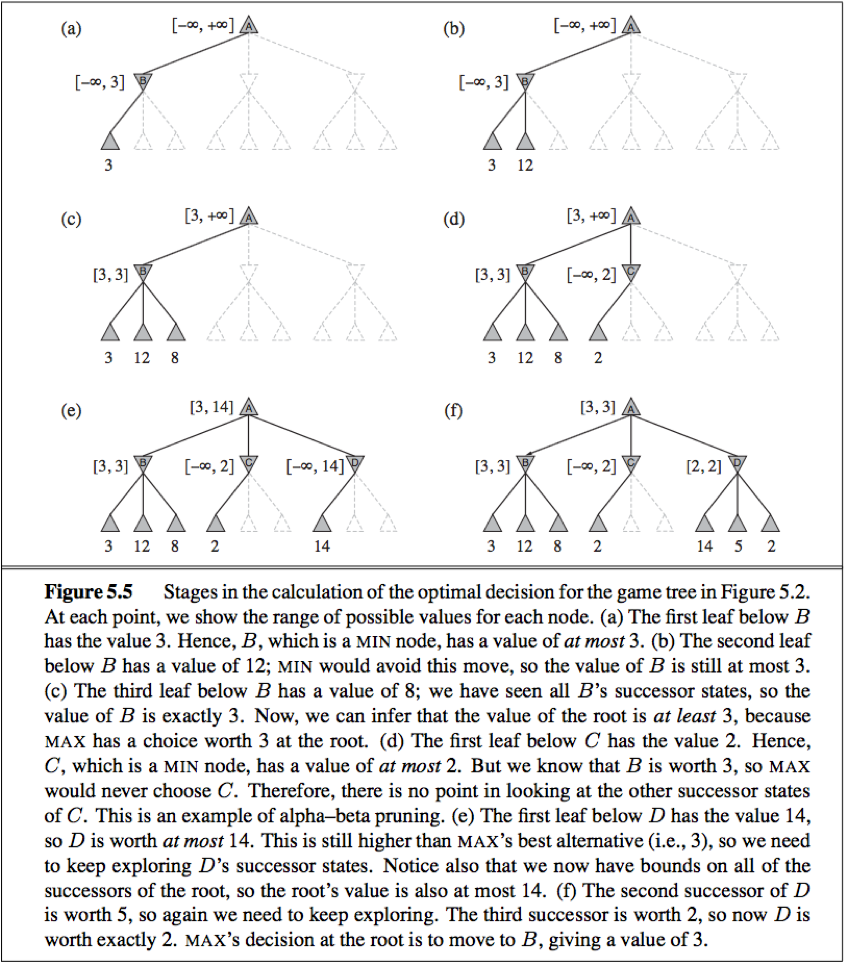
Alpha-beta pruning
The alpha-beta search algorithm computes the same optimal move as minimax, but achieves much greater efficiency by eliminating subtrees that are provably irrelevant.
When applied to a standard minimax tree, alpha-beta pruning returns the same move as minimax would, but prunes away branches that cannot possibly influence the final decision.
The general principle: consider a node n somewhere in the tree such that Player has a choice of moving to that node. If Player has a better choice m either at the parent node of n or any choice point further up, then n will never be reached in actual play. So once we have found out enough about n (by examining some of its descendants) to reach this conclusion, we can prune it.
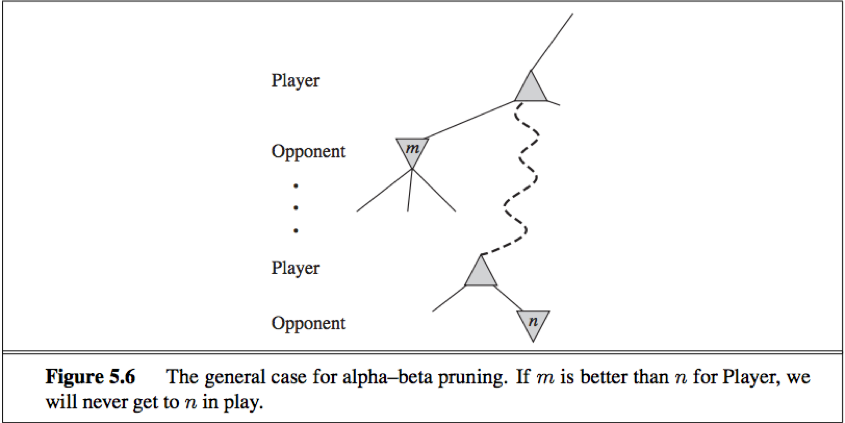
Alpha-beta search update the values of α and β as it goes along and prunes the remaining branches (i.e. terminates the recursive call) at a node as soon as the current node is known to be worse than the current α and β value for MAX or MIN, respectively.
α = the value of the best (i.e. highest-value) choice we have found so far at any choice point along the path for MAX.
β = the value of the best (i.e. lowest-value) choice we have found so far at any choice point along the path for MIN.

The effectiveness of alpha-beta pruning is highly dependent on the order in which the states are examined. The best moves are often called killer moves and to try them first is called the killer move heuristic.
Transpositions: Different permutations of the move sequence that end up in the same position. Repeated states occur frequently in many games because of transpositions.
It is worthwhile to store the evaluation of the resulting position in a hash table the first time it is encountered so that we don’t have to recomputed it on subsequent occurrences, the hash table of previously seen positions is called a transposition table. (A transposition table is essentially identical to the explored list in GRAPH-SEARCH.)
Imperfect real-time decisions
Because moves must be made in a reasonable amount of time, usually it is not feasible to consider the whole game tree (even with alpha-beta), so programs should cut the search off at some point earlier and apply a heuristic evaluation function to states in the search, effectively turning nonterminal nodes into terminal leaves.
i.e. Alter minimax or alpha-beta in 2 ways:
1) replace the utility function by a heuristic evaluation function EVAL, which estimates the position’s utility.
2) replace the terminal test by a cutoff test that decides when to apply EVAL.
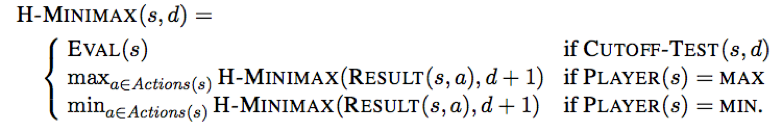
Evaluation function
An evaluation function returns an estimate of the expected utility of the game from a given position.
How do we design good evaluation functions?
1) The evaluation function should order the terminal states in the same way as the true utility function.
2) The computation must not take too long.
3) For nonterminal states, the evaluation function should be strongly correlated with the actual chances of winning.
Features of the state: Most evaluation function work by calculating various features of the state, e.g. in chess, number of white pawns, black pawns, white queens, black queens, etc.
Categories: The features, taken together, define various categories (a.k.a. equivalence classes) of states, the states in each category have the same values for all the features.
Any given category will contain some states that lead to win, draws or losses, the evaluation function can return a single value that reflects the proportion of states with each outcome.
Two ways to design a evaluation function:
a. Expected value (requires too many categories and hence too much experience to estimate) e.g.
e.g.
72% of the states encountered in the two-pawns vs. one-pawn category lead to a win(utility+!); 20% to a loss(0) and 8% to a draw(1/2).
Then a reasonable evaluation for states in the category is the expected value: (0.72*1)+(0.20*0)+(0.08*1/2)=0/76.
As with terminal states, the evaluation function need not return actual expected values as long as the ordering of the sates is the same.
b. weighted linear function (most evaluation function use that.)
We can compute separate numerical contributions from each feature and then combine them to find the total value.
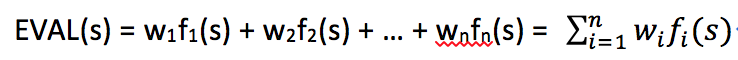
Each wi is a weight and each fi is a feature of the position. For chess, the fi could be the numbers of each kind of piece on the board (i.e. feature), and wi could be the values of the pieces (1 for pawn, 3 for bishop, etc.).
Adding up the values of features in fact involves a strong assumption (that the contribution of each feature is independent of the values of the other features), thus current programs for games also use nonlinear combinations of features.
Cutting off search

To modify ALPHA-BETA-SEARCH:
1) Replace the two lines that mention TERMINAL-TEST with
If CUTOFF-TEST(state, depth) then return EVAL(state)
2) Arrange for some bookkeeping so that the current depth is incremented on each recursive call.
The most straightforward approach: set a fixed depth limit so that CUTOFF-TEST(state, depth) returns true for all depth greater than some fixed depth d.
A more robust approach: apply iterative deepening.
quiescence search: The evaluation function should be applied only to position that are quiescent ( i.e. unlikely to exhibit wild swing in value in the near future). Nonquiescent positions can be expanded further until quiescent positions are reached, this extra search is called a quiescence search.
Horizon effect: arises when the program is facing an opponents move that causes serious damage and is ultimately unavoidable, but can be temporarily avoided by delaying tactics.
Singular extension: One strategy to mitigate the horizon effect, a move that is “clearly better” than all other moves in a given position. Once discovered anywhere in the tree in the course of a search, the singular move is remembered. When the search reaches the normal depth limit, the algorithm checks to see if the singular extension is a legal move; if it is, the algorithm allows the move to be considered.
Forward pruning
Forward pruning: Some moves at a given node are pruned immediately without further consideration.
PROBCUT (probabilistic) algorithm: A forward-pruning version of alpha-beta search that uses statistic gained from prior experience to lessen the chance that the best move will be pruned.
Alpha-beta search prunes any node that is provably outside the current(α, β) window, PROBCUT also prunes nodes that are probably outside the window. It computes this probability by doing a shallow search to compute the backed-up value v of a node and then using past experience to estimate how likely it is that a score of v at depth d in the tree would be outside (α, β).
Search versus lookup
Many game programs precompute tables of best moves in the opening and endgame so that they can look up a move rather than search.
For the opening (and early moves), the program use table lookup, relying on the expertise of human and statistic from a database of past games;
After about ten moves, end up in a rarely seen position, the program switch from table lookup to search;
Near the end of the game there are again fewer possible positions, and more chance to do lookup.
A computer can completely solve the endgame by producing a policy, which is a mapping from every possible state to the best move in that state. Then we can just look up the best move rather than recomputed it anew.
Stochastic games
Stochastic games: Games mirror unpredictability by including a random element, such as the throwing of dice.
Game of chance can be handled by an extension to the minimax algorithm that evaluates a chance node by taking the average utility of all its children, weighted by the probability of each node.

The game tree in backgammon (a stochastic game) include chance nodes. The branches leading from each chance node denote the possible dice roll.
Expectiminimax value: Positions in stochastic games do not have definite minimax values, we can only calculate the expected value of a position (the average over all possible outcomes of the chance nodes, weighted by the probability of each chance action).
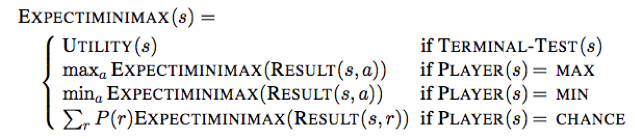
r represents a possible dice roll (or other chance event);
RESULT(s,r) is the same state as s, with additional fact that the result of the dice roll is r.
Evaluation function for games of chance
When uncertainty is involved, the evaluation function must be a positive linear transformation of the probability of winning from a position (or of the expected utility of the position).
If the program knew in advance all the dice rolls that would occur for the rest of the game,
Time complexity: O(bmnm), b is the branching factor, m is the maximum depth of the game tree, n is the number of distinct rolls.
Alpha-beta pruning in stochastic games: Alpha-beta pruning can be applied to game trees with chance nodes. The analysis for MIN and MAX node is unchanged, chance nodes can be pruned by putting bounds on the possible values of the utility function of all its children, arriving at bounds for the average (value of the chance node).
Monte Carlo simulation: Start with an alpha-beta search algorithm. From a start position, have the algorithm play thousands of games against itself, using random dice rolls.
Partially observable games
Optimal play in games of imperfect information, such as Kriegspiel and bridege, requires reasoning about the current and future belief states of each player. A simple approximation can be obtained by averaging the value of an action over each possible configuration of missing information.
Kriegspiel
Kriegspiel: a partially observable variant of chess in which pieces can move but are completely invisible to the opponent.
Belief state: The set of all logically possible board states given the complete history of percepts to date.
Keeping track of the belief state as the game progresses is exactly the problem of state estimation.
Strategy: Instead of specifying a move to make for each possible move the opponent might make we need a move for every possible percept sequence that might might be received.
Guaranteed checkmate/Winning strategy: One that for each possible percept sequence, leads to an actual checkmate for every possible board state in the current belief state, regardless of how the opponent moves.
The general AND-OR search algorithm can be applied to the belief-state space to find guaranteed checkmates.
Probabilistic checkmate: Such checkmates are still required to work in every board state in the belief state; they are probabilistic with respect to randomization of the winning player’s moves.
Card games
Card games: where the missing information is generated randomly.
An effective algorithm: consider all possible deals of the invisible cards; solve each one as if it were a fully observable game; then choose the move that has the best outcome averaged over all the deals.
Suppose that each deal s occurs with probability P(s), the move we want is
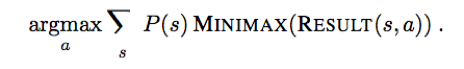
Monte Carlo approximation: instead of adding up all the deals, we take a random sample of N deals, where the probability of deal s appearing in the sample is proportional to P(s):
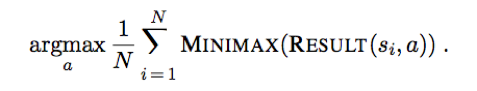
Alternative approach
Standard approach: based on minimax, evaluation functions and alpha-beta.
Alternatives:
1. heuristic minimax: Select an optimal move in a given search tree provided that the leaf node evaluations are exactly correct. But in reality, evaluations are usually crude estimate of the value of a position and can be considered to have large errors associated with them.
2. The search algorithm that generates the tree: A good search algorithm should select node expansions of high utility—ones that are likely to lead to the discovery of a significantly better move. If there are no node expansions whose utility is higher than their cost, then the algorithm should stop searching and make a move.
4. The nature of search itself: To combine the two kinds of algorithms into a robust and efficient system. A. Algorithms for heuristic search and for game playing generate sequences of concrete states; b. goal-directed reasoning or planning used by humans, sometimes eliminate combinatorial search altogether.