题目链接
解题思路
提供一种打表新思路
先来证明一个其他题解都没有证明的结论:(ans[i])是可由(ans[i-1])线性递推的。
((ans[i])表示(i)个盘子全部移走的步数)
感谢keytoyzi神仙的神仙思路
首先,在最初两层移动的时候,遵循的移动顺序规则是题中所给的顺序。
在(n)个盘子都在(A)柱的时候,我们是怎么做的呢?
先把前(n-1)个盘子按照遵循初始顺序规则的方法移动到(B)或(C);
再对第(n)个盘子进行操作;
再进行某些操作(后文会展开);
最后所有盘子移动到(B)或者(C)。
这等价于:
每一层对应一个新规则,把前(n-1)层盘子看做一层,那就相当于按照这个新的规则移动一个两层的东西。
这个新规则是啥意思呢?光说理论太难以理解,上图:

解释一下:(n-1)代表前(n-1)个盘子,这些盘子根据初始规则可能移动到(B)或者(C),而把他们看做一个整体后,相当于上图的遵循初始规则的移动方式,而这种新的移动方式,就是一个新的规则。
再来两张状态转移的图:
(单箭头表示这一步操作优先级高于另一侧)
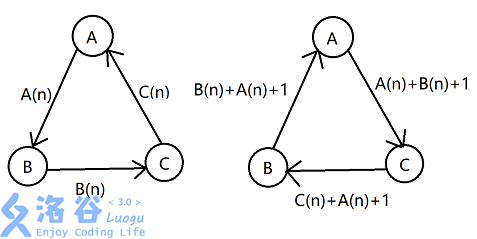
解释一下这张图。
刚开始对于前(n)个盘子形成的新规则:
(AB>AC),(BC>BA),(CA>CB)。
根据这个规则进行第(n+1)层的操作:(以(A o C)为例)
先把(A)上的前(n)个盘子扔到(B)上;((A(n)))
再把(A)最底下的第(n+1)个盘子扔到(C)上;((1))
再把扔到(B)上的前(n)个盘子扔到(C)上。((B(n)))
故总步骤数为(A(n)+1+B(n))。
同理,那么这就给出了一组递推关系。
易得,如果(n)满足左图,则(n+1)满足右图;
如果(n)满足右图,则(n+1)满足左图。
也就是说,这两张图中的状态可以互相转换。
又,(ABC)是等价的,故这张图对应了一种可能的答案(答案(1))。

这张图更复杂一些,不过实质和刚刚的相同。
以(A o B)为例。
先把(A)上的前(n)个盘子扔到(B)上;((A(n)))
再把(A)最底下的第(n+1)个盘子扔到(C)上;((1))
再把(A)上的这n个盘子扔回(A)上;((B(n)))
再把(C)上的第n+1个盘子扔到(B)上;((1))
再把(A)上的那(n)个盘子扔回(B)上。((B(n)))
故总步骤数为(A(n)+1+B(n)+1+B(n))。
同理易得,如果n满足左图,则n+1满足右图;
如果(n)满足右图,则(n+1)满足左图。
也就是说,这两张图中的状态还是可以互相转换。
而在这张图上,(AB)是等价的,(C)是另一种情况,故这张状态图对应了两种可能的答案:
(AB)对应的状态为初始(A)柱(答案(2))
或
(C)对应的状态为初始(A)柱(答案(3))。
好,那么现在对应这三种情况做一种简单的分析。
对于第一种答案:
(ABC)等价,故(A(n)=B(n)=C(n)=ans_1[n])
由图中的递推公式,(ans_1[n+1]=ans_1[n]*2+1)
对于第二种答案:
(AB)等价,(A(n)=B(n)=ans_2[n])
(ans_2[n+1]=ans_2[n]*3+2)
对于第三种答案:
(AB)等价,(A(n)=B(n)=ans_2[n])
(ans_3[n+1]=ans_2[n]+ans_3[n]+1)
这是一个线性表达式。
证毕。
所以,我们只需要知道移动一个盘子、两个盘子、三个盘子的情况,即可知道递推公式进而求解。
手动模拟打表,容易得到以下结果:
((ans[i])表示i个盘子全部移走的步数)
一个盘子:
(ans[1]=1)
两个盘子:
((1)AB>AC)
①(BC>BA),(ans[2]=3)
②(BC<BA),(ans[2]=5)
((2)AB<AC)
这里可以看做把(BC)柱子换了个位置
①(ans[2]=3):原(BC>BA),把(BC)换了个位置后变成(CB>CA)
②(ans[2]=5):原(BC<BA),同理变成(CB<CA)
三个盘子:
((1)AB>AC)
①(BC>BA)
((i)CB>CA),(ans[3]=9)
((ii)CB<CA),(ans[3]=7)
②(BA>BC)
(ans[3]=17)
((2)AB<AC)
同理,不再赘述
下附递推AC代码:
#include<stdio.h>
char a[4];
int seq[3][3];
long long ans[40];
int main(){
int i,n;
scanf("%d",&n);
for(i=0;i<6;i++){
scanf("%s",a);
seq[a[0]-'A'][a[1]-'A']=6-i;
}
if(seq[0][1]>seq[0][2]){//AB>AC
if(seq[1][2]<seq[1][0]){//BC<BA
ans[2]=5;ans[3]=17;
}else{
if(seq[2][0]>seq[2][1]){//CA>CB
ans[2]=3;ans[3]=7;
}else{
ans[2]=3;ans[3]=9;
}
}
}else{//AB<AC
if(seq[2][1]<seq[2][0]){//CB<CA
ans[2]=5;ans[3]=17;
}else{
if(seq[1][0]>seq[1][2]){//BA>BC
ans[2]=3;ans[3]=7;
}else{
ans[2]=3;ans[3]=9;
}
}
}
ans[1]=1;
int b=(ans[2]*ans[2]-ans[1]*ans[3])/(ans[2]-ans[1]);
int k=(ans[2]-b)/cnt1;
for(i=4;i<=n;i++)ans[i]=ans[i-1]*k+b;
printf("%lld",ans[n]);
return 0;
}
其实,这已经没有必要写成递推形式了。我们在讨论三种答案的时候,其实已经可以手算算出三种情况的O(1)表达式了。
来一发最短AC代码
#include<stdio.h>
#include<math.h>
typedef long long ll;
char a[4];
int s[9],p,n,i=6;
ll f(int x){
if(x==1)return (ll)2*pow(3,n-1)-1;
if(x)return (ll)pow(2,n)-1;
return (ll)pow(3,n-1);
}
int main(){
scanf("%d",&n);
while(i--)scanf("%s",a),s[(a[0]-'A')*3+a[1]-'A']=i;
if(s[1]>s[2]){
if(s[5]<s[3])p=1;
else if(s[6]>s[7])p=2;
}else if(s[7]<s[6])p=1;
else if(s[3]>s[5])p=2;
printf("%lld",f(p));
return 0;
}