题目传送门:AtCoder Grand Contest 002。
A - Range Product
略。
#include <cstdio>
int A, B;
int main() {
scanf("%d%d", &A, &B);
if (A <= 0 && B >= 0) puts("Zero");
else if (A > 0 || (B - A) & 1) puts("Positive");
else puts("Negative");
return 0;
}
B - Box and Ball
在任意时刻,维护 (mathrm{num}[i]) 表示第 (i) 个盒子内的球数,(mathrm{typ}[i]) 表示第 (i) 个盒子内是否有红球:(0) 一定没有,(1) 一定有,(2) 两种都有可能。
转移显然,最终 (mathrm{typ}) 非零的位置的个数就是答案。
#include <cstdio>
const int MN = 100005;
int N, M, Ans;
int num[MN], typ[MN];
int main() {
scanf("%d%d", &N, &M);
for (int i = 1; i <= N; ++i)
num[i] = 1, typ[i] = i == 1;
for (int i = 1; i <= M; ++i) {
int x, y;
scanf("%d%d", &x, &y);
if (num[x] == 1) {
if (typ[x] == 1) typ[y] = 1;
else if (typ[x] == 2) typ[y] = 2;
typ[x] = 0;
} else if (typ[x] != 0) typ[x] = typ[y] = 2;
--num[x], ++num[y];
}
for (int i = 1; i <= N; ++i) if (typ[i]) ++Ans;
printf("%d
", Ans);
return 0;
}
C - Knot Puzzle
把操作过程倒过来,相当于每次合并两个相邻的,需要保证合并后的长度至少为 (L)。
如果任意两个相邻的长度之和都比 (L) 小的话那一定无解,否则第一次合并那两个然后一直向左向右合并完即可。注意倒序输出。
#include <cstdio>
const int MN = 100005;
int N, L, A[MN];
int main() {
scanf("%d%d", &N, &L);
for (int i = 1; i <= N; ++i) scanf("%d", &A[i]);
int ok = 0;
for (int i = 1; i < N; ++i) if (A[i] + A[i + 1] >= L) ok = i;
if (!ok) return puts("Impossible"), 0;
puts("Possible");
for (int i = 1; i < ok; ++i) printf("%d
", i);
for (int i = N - 1; i >= ok; --i) printf("%d
", i);
return 0;
}
D - Stamp Rally
对询问做整体二分,用可撤销并查集维护连通性以及连通块大小,时间复杂度为 (mathcal O ((M + Q) log M log N))。
#include <cstdio>
#include <algorithm>
const int MN = 100005, MM = 100005, MQ = 100005;
int N, M, a[MM], b[MM];
int Q, x[MQ], y[MQ], z[MQ], p[MQ], ans[MQ];
int par[MN], siz[MN], stk[MN], tp;
inline int fp(int u) {
while (par[u]) u = par[u];
return u;
}
inline void merge(int u, int v) {
u = fp(u), v = fp(v);
if (u == v) return ;
if (siz[u] < siz[v]) std::swap(u, v);
par[v] = u, siz[u] += siz[v];
stk[++tp] = v;
}
inline void undo(int k) {
while (tp > k) {
int v = stk[tp--];
siz[par[v]] -= siz[v];
par[v] = 0;
}
}
int tmp[MQ];
void Solve(int l, int r, int s, int t) {
if (s > t) {
for (int i = l; i <= r; ++i) merge(a[i], b[i]);
return ;
}
if (l == r) {
for (int i = s; i <= t; ++i) ans[p[i]] = l;
merge(a[l], b[l]);
return ;
}
int mid = (l + r) >> 1, now = tp;
for (int i = l; i <= mid; ++i) merge(a[i], b[i]);
int s_ = s, t_ = t;
for (int i = s; i <= t; ++i) {
int u = fp(x[p[i]]), v = fp(y[p[i]]);
int sum = u == v ? siz[u] : siz[u] + siz[v];
if (sum >= z[p[i]]) tmp[s_++] = p[i];
else tmp[t_--] = p[i];
}
undo(now);
for (int i = s; i <= t; ++i) p[i] = tmp[i];
Solve(l, mid, s, t_);
Solve(mid + 1, r, s_, t);
}
int main() {
scanf("%d%d", &N, &M);
for (int i = 1; i <= M; ++i) scanf("%d%d", &a[i], &b[i]);
scanf("%d", &Q);
for (int i = 1; i <= Q; ++i) scanf("%d%d%d", &x[i], &y[i], &z[i]), p[i] = i;
for (int i = 1; i <= N; ++i) siz[i] = 1;
Solve(1, M, 1, Q);
for (int i = 1; i <= Q; ++i) printf("%d
", ans[i]);
return 0;
}
E - Candy Piles
每次操作删除最大的一堆,或者把所有堆的石子数量减一。
如果把 (a) 数组从小到大排序,然后把每一堆的石子摞起来,就像这样:

那么每次操作就相当于删除最右侧一列或最底部一行,删光了的输掉游戏。
那么就相当于初始时棋子在右下角,每次能向上或向左一格,谁走出了边界谁就输了。
我们直接用博弈论中最简单的 PN 态转换来做:P 态(Previous)就是先手必败态,N 态(Next)就是先手必胜态。
我们规定浅粉色区域(边界外)都是 N 态。所有转移都只能到 N 态的就是 P 态,只要有一种转移能到 P 态的就是 N 态。
染完色就是这样(金色是 P 态,粉色是 N 态):
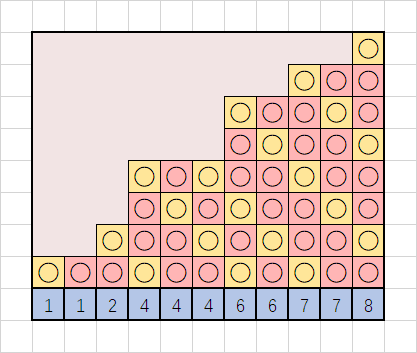
我们无法求出每个格子的状态,但是观察发现:对于每一列,不存在连续两个相邻的 P 态,不存在三个相邻的 N 态。
而且我们还发现,对于相邻两列,左边一列的颜色向下移动一格,就与右边一列的颜色完全一致。
这两个结论读者可以自行证明,因为都不难这里不再赘述。
我们考虑从左向右按列递推,假设当前是第 (i) 列,前一列的高度为 (a_{i - 1}),这一列的高度为 (a_i)。
我们记录每一列的,连续两个 N 态的位置,如上图倒数第二列就是 ({1, 4}) 这两个位置,最后一列就是 ({3, 6}) 这两个位置。
但是这些位置一直在变化,但是可以发现:基本上都是每次减 (1),然后加入或删除一些位置。
那么我们可以存储这些位置加上 (i) 的值,比如此时位置为 (p),存储 (p + i),到下一列时位置即为 ((p + i) - (i + 1) = (p - 1))。
接下来处理加入新的一列 (a_i) 时会发生什么:
如果 (a_{i - 1} = a_i),则仅仅是左边的状态向下移动了一格,然后在最顶上加入一个 P 态而已。否则 (a_{i - 1} < a_i):
对于 (a_i) 超出 (a_{i - 1}) 的部分,是从第 (a_i) 高度为 P 态开始,往下依次为 PN 态交替,这一部分没有连续两个 N 态。
那么考虑高度为 (a_{i - 1} + 1) 时的状态:它会和前一列的高度为 (a_{i - 1}) 的状态共同影响该列的高度为 (a_{i - 1}) 的状态。
这可以直接通过 (a_i - a_{i - 1}) 的奇偶性算出。如果它的状态和前一列的高度为 (a_{i - 1}) 的状态相同,则不会产生任何相邻的 N 态。否则:
如果它的状态是 P,前一列状态是 N,比如上图中高度为 ([6, 7]) 的相邻两列,就会在 (a_{i - 1} - 1) 高度处产生相邻的 N 态。
如果它的状态是 N,前一列状态是 P,比如上图中高度为 ([4, 6]) 的相邻两列,就会在 (a_{i - 1}) 高度处产生相邻的 N 态。
也就是说,每次只会加入最多一个新的相邻的 N 态,而且高度总是比之前的高。
那么我们可以用一个队列来维护这些连续的 N 态的位置:每次加入新的,如果最低的那个低于高度 (1) 了就把它去掉。
再来一个变量 (mathrm{lstc}) 表示高度为 (a_i) 时的状态,代码中 (0) 表示 P 态,(1) 表示 N 态。就可以实现转移和求最终答案了。
时间复杂度为 (mathcal O (N))。
#include <cstdio>
#include <algorithm>
const int MN = 100005;
int N, A[MN];
int que[MN], l, r;
int main() {
scanf("%d", &N);
for (int i = 1; i <= N; ++i) scanf("%d", &A[i]);
std::sort(A + 1, A + N + 1);
l = 1, r = 0;
int lstc = 0;
for (int i = 2; i <= N; ++i) {
if (A[i] == A[i - 1]) lstc ^= 1;
else {
int c = ~(A[i] - A[i - 1]) & 1;
if (c != lstc) que[++r] = A[i - 1] - lstc + i;
lstc = 0;
}
while (l <= r && que[l] <= i) ++l;
}
puts(lstc ^ (A[N] & 1) ^ ((r - l) & 1) ? "First" : "Second");
return 0;
}
F - Leftmost Ball
我们直接对最终的那个产生出的序列进行计数。
如果 (N = 1) 或 (K = 1),直接输出 (1) 即可。
那么现在序列中至少有 (1) 和 (2) 两个非零元素了。
可以发现把序列中非零的数的值做一个置换(也就是 (1) 变 (2),(2) 变 (3),(3) 变 (1) 这种),序列仍然合法。
那么我们强制计数字典序最小的那种序列的个数,最后把答案乘以 (N!) 输出即可。
也就是说,必须先出现 (1) 再出现 (2),先出现 (2) 再出现 (3),以此类推。
再考虑关于 (0) 的合法性:(1) 必须在第一个 (0) 之后出现,(2) 必须在第二个 (0) 之后出现,以此类推。
也就是:记第 (i) 个 (0) 的位置为 (p_i),以及 (i) 的第一次出现位置为 (q_i)。有:
- (p_{i - 1} < p_i)。
- (q_{i - 1} < q_i)。
- (p_i < q_i)。
当然还有对于每个颜色 (i in [1, N]),它的后 (K - 2) 次出现,必须按照顺序。
似乎都是废话,但是其实此时我们已经把问题转化成了,求一张图的拓扑排序的数量的问题:

上图中,有 (K) 行,和 (N) 列。
注意到第一个点必须是最左边的 (0),然后接下来可以选第二个 (0) 或者最上面的 (1)。
如果选了最上面的 (1),那下面那条长度为 (K - 2) 的跟着的链可以直接以组合数的形式乘到答案里,然后删掉,变成少第一列的情况。
如果选了第二个 (0),又变成能选 (1) 或第三个 (0)。如果此时选了 (1),就变成能选 (2) 或第三个 (0) 的情况。以此类推。
可以发现这个结构是可以 DP 的。
令 (mathrm{f}[i][j]) 表示目前 (0) 剩下靠后的 (i) 个,有颜色的点剩下靠后的 (j) 列时的方案数。此时必须有 (j ge i)。转移显然:
答案即为 (mathrm{f}[N][N]),时间复杂度为 (mathcal O (NK + N^2))。
#include <cstdio>
typedef long long LL;
const int Mod = 1000000007;
const int MN = 2005, MS = 4000005;
inline int qPow(int b, int e) {
int a = 1;
for (; e; e >>= 1, b = (LL)b * b % Mod)
if (e & 1) a = (LL)a * b % Mod;
return a;
}
int Fac[MS], iFac[MS];
inline void Init(int N) {
Fac[0] = 1;
for (int i = 1; i <= N; ++i) Fac[i] = (LL)Fac[i - 1] * i % Mod;
iFac[N] = qPow(Fac[N], Mod - 2);
for (int i = N; i >= 1; --i) iFac[i - 1] = (LL)iFac[i] * i % Mod;
}
inline int Binom(int N, int M) {
return (LL)Fac[N] * iFac[M] % Mod * iFac[N - M] % Mod;
}
int N, K;
int f[MN][MN];
int main() {
scanf("%d%d", &N, &K);
if (K == 1 || N == 1) return puts("1"), 0;
Init(N * K);
f[0][0] = 1;
for (int j = 1; j <= N; ++j) f[0][j] = (LL)f[0][j - 1] * Binom(j * (K - 1) - 1, K - 2) % Mod;
for (int i = 1; i <= N; ++i) {
f[i][i] = f[i - 1][i];
for (int j = i + 1; j <= N; ++j)
f[i][j] = (f[i - 1][j] + (LL)f[i][j - 1] * Binom(i + j * (K - 1) - 1, K - 2)) % Mod;
}
printf("%lld
", (LL)f[N][N] * Fac[N] % Mod);
return 0;
}