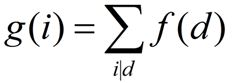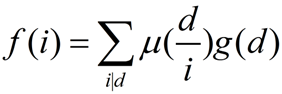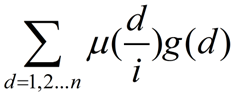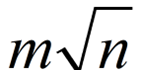【Gcd】

【题目描述】

有 n 个正整数 x1~xn，初始时状态均为未选。有 m 个操作，每个操作给定一个编号 i，将 xi 的选取状态取反。每次操作后，你需要求出选取的数中有多少个互质的无序数对。

【输入数据】

第一行两个整数 n,m。第二行 n 个整数 x1~xn。接下来 m 行每行一个整数。

【输出数据】

m 行，每行一个整数表示答案。

【样例输入】

4 5 1 2 3 4 1 2 3 4 1

【样例输出】

0 1 3 5 2

【数据范围】

对于 20%的数据，n,m<=1000。对于另外 30%的数据，xi<=100。对于 100%的数据，n,m<=200000，xi<=500000，1<=i<=n。

分析：
对带有询问修改的问题我们可以先想出无询问无修改的问题解决方法，然后将解法组织成易于修改和回答询问的形式。

那么对于这道题，无修改无询问则是：给出n个数,求出n个数中互质的无序数对个数。

让我们考虑互质的本质——没有大于1的公因子,即GCD(a,b)==1。这样的数学题我们清楚地知道一一枚举是没有好结果的，通常情况下这类问题可以朝两大方向思考：组合数与容斥原理。

由于本题不存在方案数、概率等的计算,因此我们尝尝容斥原理的味道。

既然企图使用容斥，那么定几个表示有关联数组是很有必要的：
·f(i)表示GCD为i的数对个数

·g(i)表示GCD为i的倍数的数对个数

·s(i)表示为i的倍数的数的个数

接下来要做的就是一步步地走向答案。我们可以很轻松地获得s(i)的值，具体方法为枚举每个数的因数，然后s(该因数)++。s(i)的妙处其实更多体现在它的这个用途：g(i)=s(i)*(s(i)-1)/2——据此无意间得到了g(i)的值(式子表示i的倍数相互组合形成二元组，那么这些二元组的gcd一定为i的倍数)。

按照上文的步子，我们现在应该去寻找g(i)与f(i)的关系了。我们可以发现所有的f(j)(j为i的倍数)的值加起来就等于g(i),用式子表示为：

然后到这里一部分人会蒙，一部分人会开心……可能是因为他们之间相差了一个叫做莫比乌斯反演的东西。

由于上面已经很明显是第二类莫比乌斯反演的式子，因此变形为：

到这里后一切都得以解决：由于我们最终要求f(1)所以我们得出一个很关键很常用的结论：

在范围内，GCD为1的数对个数为：

啊等一下好像还有询问修改操作没有处理呢。好吧具体处理方式为对于每个新加入或者新删除的数，枚举它的因数来修改s()的值。s()的值修改了自然可以轻松修改g()的值，g()的值修改了就将ans减去原来的式子加上现在的新 g()的值。由于枚举因数时间复杂度为根号n，因此最终时间复杂度为

代码在下面：(莫比的线筛大米饼有写)

 1 #include<stdio.h>
 2 #define ll long long
 3 #define go(i,a,b) for(int i=a;i<=b;i++)
 4 const int N=500003;
 5 int n,m,a[N],I,x,d,Mob[N];
 6 ll s[N],g[N],f[N],ans;bool get[N];
 7 struct Sieve
 8 {
 9     int prime[N],t;bool no[N];
10     void Mobius_Sieve()
11     {
12         Mob[1]=1;
13         go(i,2,500000){if(!no[i])Mob[prime[++t]=i]=-1;
14         go(j,1,t){if(1ll*prime[j]*i>500000)break;
15         Mob[i*prime[j]]=i%prime[j]?-Mob[i]:0;
16         no[i*prime[j]]=1;if(i%prime[j]==0)break;}}
17     }
18 }Tool;
19 int main()
20 {    
21     Tool.Mobius_Sieve();
22     scanf("%d%d",&n,&m);
23     go(i,1,n)scanf("%d",a+i);
24     while(m--)
25     {
26         scanf("%d",&I);x=a[I];
27         d=(get[I]^=1)?1:-1;
28         go(i,1,x)if(x%i==0&&i*i<=x)
29         {
30             s[i]+=d;if(i!=x/i)
31             s[x/i]+=d;
32             
33             ans-=Mob[i]*g[i];if(i!=x/i)
34             ans-=Mob[x/i]*g[x/i];
35             
36             g[i]=s[i]*(s[i]-1)/2;if(i!=x/i)
37             g[x/i]=s[x/i]*(s[x/i]-1)/2;
38             
39             ans+=Mob[i]*g[i];if(i!=x/i)
40             ans+=Mob[x/i]*g[x/i];
41         }
42         else if(i*i>x)break;
43         printf("%lld
",ans);
44     }
45     return 0;
46 }//Paul_Guderian

我常常在河边呆呆的幻想，
做着一个孩子的白日梦，
想象未来有许多颜色。————汪峰《我在长大》