在树状数组BIT后,第二篇极长的数据结构文章……
0.引入
同样的引入:神题:A+B Problem
有几种方法怕有人说我博客很水就不放了,详情参见我的这篇博客。
1.线段树简介
之前可能学过树状数组,没错,这东西,和树状数组是 几乎 (记住说明文语言要准确严谨) 互通的,不过有一点不同(这里都针对最基础的来讲),就是线段树可以查询最值,就像ST表一样(个人认为ST表的全名是Segment Tree Table))。
好了,引入正题。
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为(O(logN))。而未优化的空间复杂度为(O(2N)),实际应用时一般还要开(4N)的数组以免越界,因此有时需要离散化让空间压缩。 ——百度百科
博主语文水的很,再解释也解释不清楚了
2.代码实现
2.1. 附上(大)部分介绍
首先,上一个结构体
struct node{
int l,r;
...//这里储存你需要的各种信息
};
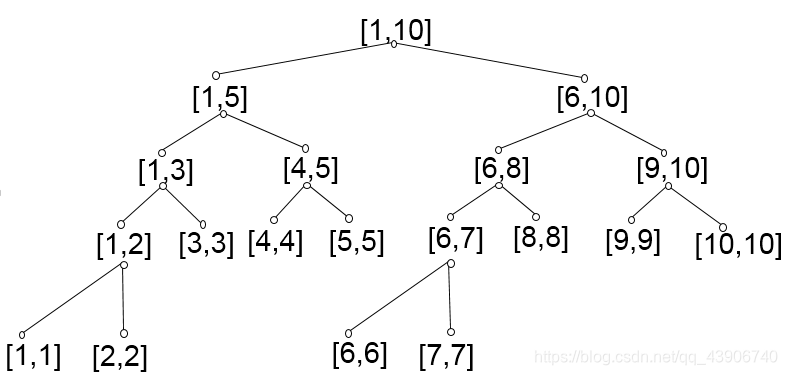
呃呃呃……不会这么简单吧……当然不会。这个只是一个线段树的节点,然后又这些节点构成一棵线段树,如图。
其实,这个图可以表示成一个线段组成的树,如下。
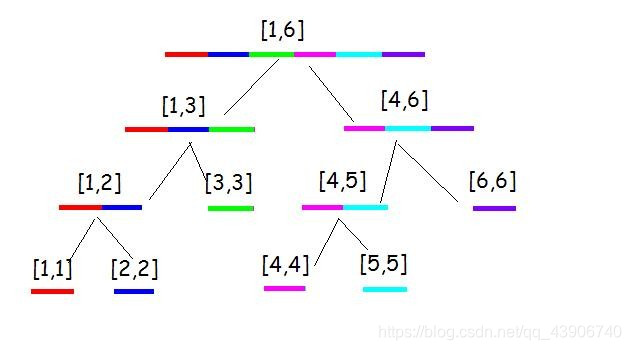
还要清楚一个区间的概念:
中括号([和])表示闭区间,就是包括边缘的区间;小括号((和))表示开区间,就是不包括边缘的区间。
另外说明一下,真正的线段树可不是这样的——这个只是表示了整数的1~6的区间,而实际上是表示的所有的区间,就是([1,2) [2,3)......)一直到([n,n+1))
额……所以,还有一个问题,就是说,有多少个节点?
按照线段树的定义,([1,n+1))的线段树有(n)个叶子结点,又因为线段树是一颗二叉树,所以线段树一共有(2*n)个节点。
不过,数组只开(2n)就够了吗?我们进行线段树的运算,是根据完全二叉树来进行计算的,所以任意一个节点(p)的左儿子就是(p*2),右儿子就是(p*2+1),对应上方区间([1,7))的线段树,可以得知,我们至少要把空间开到13(因为图中区间([4,5])最少是下标6,所以([5,5])即此区间的右儿子的下标就是13)!这时候,如果开12,那不爆才怪……
那开多少呢?(4n)。为什么?也就是多留了一层的节点出来(原来最下层(n)个节点,因为是二叉树,乘个2,再加上原来的(2n),就是(4n)了)
So,真正的线段树,是这样的
struct node{
int l,r;
...//这里储存你需要的各种信息
}tr[MAXN<<2];//后面会介绍的左移操作
好了,神奇的基础概念终于介绍完了……
2.2.基础操作
额,其实上面已经提到了——基础操作就是左儿子和右儿子!
因为线段树是一棵不太完全的完全二叉树,所以我们就可以按照完全二叉树的方式来使用线段树的左儿子和右儿子,如下
inline int ls(int p) { return p << 1; }
inline int rs(int p) { return p << 1 | 1; }
嗯?好像和上面的写法不一样?
为什么要这样写呢?因为位运算节省时间啊!
为什么是对的呢?因为(x<<1)就和(x*2)一样啊![1]。
Tips:使用位运算一定要多打括号,因为位运算的优先级,很玄学,比加减乘除都还低……
当然,就算用了inline,函数还是有调用时间的,更常用的做法是宏定义。
#define ls(p) ( p << 1 )
#define rs(p) ( p << 1 | 1 )
2.3.延伸操作
以下操作都是在同一个背景下——单点修改+区间求和
首先,为了做这个操作,我们需要这样的一个结构体:
struct node{
int l,r;
long long sum;
};
这个sum,指的是区间l~r范围内的和。
2.3.1.建树
树状数组都不用这东西,怪不得很多人都只打树状数组,不打线段树
2.3.1.1.实现
怎么建树呢?等一下,不要想复杂了,线段树的建树就是给每一个节点附上初始值。
inline void build(int p,int l,int r) {
tr[p].l=l; tr[p].r=r; tr[p].sum=0;
if(l==r) { return ; }
int mid=(l+r)>>1;
build(ls(p),l,mid);
build(rs(p),mid+1,r);
}
2.3.1.2.分析
天哪!什么东西!真是短小精悍!
好吧,简而言之,build(p,l,r)的意思是,将下标为(p)的这个区间的左端点赋值为(l),右端点赋值为(r)。
有没有清楚一点了?那为什么要从中间建树呢?因为要让这棵树尽量接近完全二叉树,这样才能更方便快捷地查找啊!
2.3.1.3.时间复杂度
没有什么好说的……要便利每一个节点,而线段树一共有(n*2)个节点,所以时间复杂度为(O(n))
2.3.1.4.(必须要看的)拓展
很多情况下,我们需要的是一个初始化过的线段树,但是如果写一个修改的话,复杂度是(O(n log n))的,但是线段树在这里可以优于树状数组——它只需要(O(n))的时间复杂度。
设已经输入的初始化数组为(a),则有如下代码
int a[MAXN];
inline void build(int p,int l,int r) {
tr[p].l=l; tr[p].r=r;
if(l==r) { tr[p].sum=a[l]; return ; }
int mid=(l+r)>>1;
build(ls(p),l,mid);
build(rs(p),mid+1,r);
tr[p].sum=tr[ls(p)].sum+tr[rs(p)].sum;
}
为啥?区间长度都为1了,你还能干啥?这个区间就是(a_l)了嘛(反正(l)都等于(r))
所以,该区间的区间和就是两个子区间的和。
2.3.2.查找
先把查找说了吧……
2.3.2.1实现
inline long long query(int p,int l,int r) {//l到r的区间和
if(l<=tr[p].l&&r>=tr[p].r) return tr[p].sum;
if(tr[p].l>r||tr[p].r<l) return 0;
long long ans=0;
ans+=query(ls(p),l,r);
ans+=query(rs(p),l,r);
return ans;
}
2.3.2.2.分析
首先,前两句是最容易看懂的,分别代表两种情况——当前节点代表的区间被查询的这个区间完全包含或完全不包含。
肯定完全包含就返回所有的和,完全不包含就返回0,因为没有一个元素属于查询的区间
至于后面的,也很好懂,就是说,在左儿子的区间里和右儿子的区间里查询,求总和。
2.3.2.3.时间复杂度
有没有神似归并排序?没错。又因为每一次操作为(O(1)),又加上(O(log n))的递归操作,复杂度就是(O(log n))
2.3.3.修改
2.3.3.1.实现
#define dist(p) (tr[p].r-tr[p].l+1)
inline void update(int p,int k,int delta) {
if(tr[p].l==k&&tr[p].r==k) {
tr[p].sum+=dist(p)*delta;
return ;
}
if(tr[p].l>k||tr[p].r<k) return ;
update(ls(p),k,delta);
update(rs(p),k,delta);
tr[p].sum=tr[ls(p)].sum+tr[rs(p)].sum;
}
2.3.3.2.分析
同上……
说一下(dist),就是当前区间的长度……
2.3.3.3.时间复杂度
同上……
2.3.4.变值
其实可以看作修改的变种……
2.3.4.1.实现
inline void change(int p,int k,int delta) {
if(tr[p].l==k&&tr[p].r==k) {
tr[p].sum=delta;
return ;
}
if(tr[p].l>k||tr[p].r<k) return ;
change(ls(p),k,delta);
change(rs(p),k,delta);
tr[p].sum=tr[ls(p)].sum+tr[rs(p)].sum;
}
2.3.5.总汇
struct node{
int l,r;
int sum;
}tr[MAXN<<2];
int a[MAXN];
#define ls(p) ( p << 1 )
#define rs(p) ( p << 1 | 1 )
inline void build(int p,int l,int r) {
tr[p].l=l; tr[p].r=r;
if(l==r) {
tr[p].sum=a[l];
return ;
}
int mid=(l+r)>>1;
build(ls(p),l,mid);
build(rs(p),mid+1,r);
tr[p].sum=tr[ls(p)].sum+tr[rs(p)].sum;
}
inline void update(int p,int k,int delta) {
if(tr[p].l==k&&tr[p].r==k) {
tr[p].sum+=delta;
return ;
}
if(tr[p].l>k||tr[p].r<k) return ;
update(ls(p),k,delta);
update(rs(p),k,delta);
tr[p].sum=tr[ls(p)].sum+tr[rs(p)].sum;
}
inline int query(int p,int l,int r) {
if(tr[p].l>=l&&tr[p].r<=r)
return tr[p].sum;
if(tr[p].l>r||tr[p].r<l) return 0;
int sl=query(ls(p),l,r),
sr=query(rs(p),l,r);
return sl+sr;
}
2.4.线段树的优势和劣势
这里相较树状数组来说一下
2.4.1.优势
- 非常灵活,这里在后面的拓展板块会说到
- 容易理解
- 建树时间较短,变值时间较短(树状数组需要两次查询和一次修改)
2.4.2.劣势
下面给出某OJ的某道题的两种做法(上方为树状数组,下方为线段树)
2.4.2.1.时间!空间!
稍微分析可以得到,线段树常数较大,空间也大(递归空间不大?(zkw):(What are you saying?)(zkw线段树:一种用非递归实现的线段树))
下面的拓展板块会提到一些对线段树的小优化。
2.4.2.2.编码复杂度较高
作为一个压行高手,四行树状数组……
而线段树……无言……(看看上面就知道了)
3.线段树的拓展
3.1.懒标记
懒标记,是线段树最(difficult)的地方。
想要搞懂线段树,一定要把下面完全弄懂!
3.1.1.用途
用途……挺多的……
想一下,树状数组最难的是什么?区间修改+区间查询。
线段树最难的也是这个(没树状数组搞一堆难以理解的差分难)。
线段树的灵活性也来源于此。
3.1.2.定义
定义在结构体中。(下文用(tag)表示)
意义:储存一个还未下传的应该加入该区间的子区间内的和。
额……没看懂的样子……没事,结合下面的代码来吧!
3.1.3.神性——lazy操作
线段树的最关键部分,保证全部看懂!
#define dist(p) (tr[p].r-tr[p].l+1)
inline void lazy(int p) {
if(tr[p].tag&&tr[p].l!=tr[p].r) {
tr[ls(p)].sum+=tr[p].tag*dist(ls(p));
tr[rs(p)].sum+=tr[p].tag*dist(rs(p));
tr[ls(p)].tag+=tr[p].tag;
tr[rs(p)].tag+=tr[p].tag;
tr[p].tag=0;
}
}
懵不懵?
首先,明确上面的定义。其实,真的很明了。将左右儿子的和加上没下传的和,左右儿子的标记也需要继续下传,于是也把左右儿子的标记加上当前节点的标记。
算了,再结合(update)来看一看。
inline void update(int p,int l,int r,int delta) {
if(tr[p].l>=l&&tr[p].r<=r) {
tr[p].sum+=delta*dist(p);
tr[p].tag+=delta;
//因为这里就return了,没有把下面的所有区间加上delta
//但是要访问下面的区间一定会访问到这个点,于是必须要用懒标记来下传
//又因为lazy操作是O(1)的,所以时间复杂度没变
return ;
}
if(tr[p].l>r||tr[p].r<l) return ;
lazy(p);//下传
update(ls(p),l,r,delta);
update(rs(p),l,r,delta);
tr[p].sum=tr[ls(p)].sum+tr[rs(p)].sum;
}
保证理解后,尝试一下自己写出(query)
附上标程
inline int query(int p,int l,int r) {
if(tr[p].l>=l&&tr[p].r<=r) return tr[p].sum;
if(tr[p].l>r||tr[p].r<l) return 0;//因为不包括,所以直接返回0
lazy(p);//下传
return query(ls(p),l,r)+query(rs(p),l,r);
}
等一下!区间变值呢?
区间变值,需要另外一个懒标记,来储存变值的结果。如果是存在多种操作,就需要很多有关优先级的考虑,因此要复杂得多。
从这个角度上看,懒标记其实是一种用空间换时间的表现,所以如何优化空间复杂度就很重要了。
3.2.线段树的空间优化
因为我懒,就以单点修改+区间查询为例子,也就是【模板】树状数组 1……
首先,看向原来的结构体,发现——(l)和(r)好多余啊……没错,的确很多余,就可以用这个来优化一下了……
直接上完整的代码吧
const int MAXN=500001;
struct node{
int sum;
}tr[MAXN<<2];
int _l,_r;
#define ls(p) ( p << 1 )
#define rs(p) ( p << 1 | 1 )
inline void update(int p,int k,int delta) {
if(_l==k&&_r==k) {
tr[p].sum+=delta;
return ;
}
if(_l>k||_r<k) return ;
int mid=(_l+_r)>>1,R=_r;
_r=mid;
update(ls(p),k,delta);
_l=mid+1; _r=R;
update(rs(p),k,delta);
tr[p].sum=tr[ls(p)].sum+tr[rs(p)].sum;
}
inline int query(int p,int l,int r) {
if(l<=_l&&_r<=r) return tr[p].sum;
if(_l>r||_r<l) return 0;
int mid=(_l+_r)>>1,R=_r,s=0;
_r=mid;
s+=query(ls(p),l,r);
_l=mid+1; _r=R;
s+=query(rs(p),l,r);
return s;
}
#define init() {_l=1; _r=n;}
一般来说,这个是可以不用写(build)的,因为大多数都没有赋初值的操作(所以这道题刚好要写,博主懒,就直接来了)
因为无论如何都是从节点1开始搜索,按照(build)的思路,可以由这个节点的信息算出子节点的信息,因此就不用多两个累赘空间了。当然,写成函数调用参数的方式也可以,但是调用参数较慢,就不常用了。
至于(init),因为每一次要从节点1开始遍历,所以每一次操作之前都要使用一次(init)。
完整代码见此(先用普通线段树A一次吧)
3.3.区间最值
好像写错地方了……这个不应该在基础的地方吗……
【模板】ST表(不要被题目所迷惑,真的可以用线段树做,甚至空间优化都不用)
struct node{
int l,r;
long long big;
}tr[MAXN<<2];
int a[MAXN];
inline void build(int p,int l,int r) {
tr[p].l=l; tr[p].r=r;
if(l==r) {
tr[p].big=a[l];
return;
}
int mid=(l+r)>>1;
build(ls(p),l,mid);
build(rs(p),mid+1,r);
tr[p].big=max(tr[ls(p)].big,tr[rs(p)].big);
}
inline long long biggist(int p,int l,int r) {
if(l<=tr[p].l&&r>=tr[p].r) return tr[p].big;
if(tr[p].l>r||tr[p].r<l) return -0x3f3f3f3f;//因为是查询最大值,所以这里返回极小值
return max(biggist(ls(p),l,r),biggist(rs(p),l,r));
}
4.真正的优化——zkw线段树
我好蒟啊,学会了再补充吧
课件详情
膜拜大佬zkw
5.真正的拓展——高维线段树
我好蒟啊,学会了再补充吧
6.例题枚举
- A+B problem(好滑稽啊)
- 统计和(比板题还板题的板题)
- Stars(大板题)
- 【模板】树状数组 1
- 逆序对(可以看看这篇博客(可能翻得有点久),讲的是树状数组逆序对,线段树也可以用同样的方法求解)
- 【模板】树状数组 2
- 上帝造题的七分钟2(很灵活,注意使用并查集优化常数…)
- I hate it
- 【模板】ST表
- 滑稽窗口(骚年,相信你的常数)
- 【模板】线段树 1
- 开关灯
- 【模板】线段树 2(考验含优先级的线段树)
- 维护序列(上题的重题)
(x<<k)可以看做(x*2^k),(x>>k)可以看做([frac{x}{2^k}])。又因为(x*2)是偶数,而偶数的二进制最后一位是0,所以偶数(|1)就相当于(+1) ↩︎