算法期末备考-第7练-递归与分治

递归与分治

Hanoi塔问题

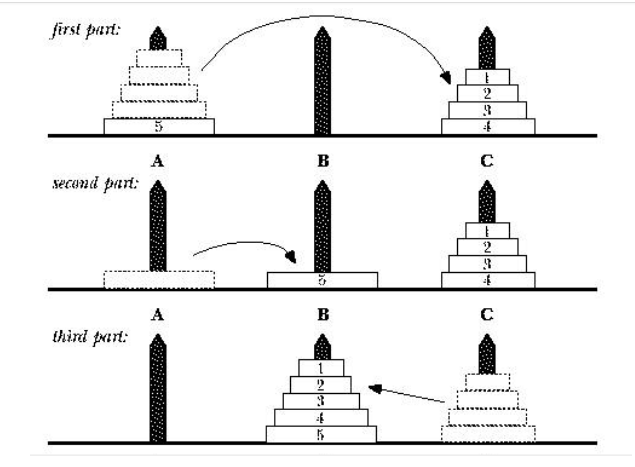
请观察上图即可，图片所显示其实就是我们处理hanoi塔的三步。

（注意：图片事网上找来的，汉诺塔问题是从 “A” 借助 “C” 转移到 “B” ）

假设f(x) ：把x个盘子全部从A借助C转移到B时所用的步数。

以上图举例子。

1、首先先把4个盘子通过B转移到C 操作步数为：f(4)

2、然后把最底层的盘子（编号为5）移动到B 操作步数为：1

3、最后把4个盘子通过A转移到B 操作步数为：f(4)

通过上述例子：

可得到：f(5) = 2*f(4)+1

随着盘子的增多,问题其实仅仅是从底层多加了delta层，但解决的步骤依旧一样。

递归计算

 1 #include<iostream>
 2 using namespace std;
 3 
 4 int Hanoi(int x){
 5     if( x == 1 )
 6         return 1 ;
 7     else
 8         return Hanoi(x-1) * 2 + 1 ;
 9 }
10 int main()
11 {
12     int n ;
13     cin >> n ;
14     cout << Hanoi(n) << endl ;
15     return 0;
16 }

递归计算汉诺塔

递归记录路径

 1 #include<iostream>
 2 using namespace std;
 3 //打印其路径
 4 void Move( char u , char v ){
 5     printf("%c -> %c
",u,v);
 6 }
 7 
 8 //起点为A , 过程中借助C , 最后到达B
 9 //( A -> C -> B )
10 void Hanoi( int n , char A , char B , char C ){
11     if( n > 0 ){
12         Hanoi( n - 1 , A , C , B );
13         Move( A , B );
14         Hanoi( n - 1 , C , B , A );
15     }
16 }
17 int main()
18 {
19     int n ;
20     cin >> n ;
21     Hanoi(n,'A','B','C');
22     return 0;
23 }

递归计算并记录路径-汉诺塔

虽然代码非常简短，但是其递归过程比较复杂。

针对每一堆盘子来说，都是分三步，

通过得知自己所在的位置，借助哪根柱子，最后要移动到哪一个柱子。

但是对于过程中的第一步，其实是递归后的结果。

Hanoi( n - 1 , A , C , B ); =>……
Move( A , B );
Hanoi( n - 1 , C , B , A );

由这句话往下到下一层

Hanoi( n - 1 , A , C , B )
                                                                        {   => …… (***)
                                        { Hanoi( n - 3 , A , C , B ) => {
   {  Hanoi( n - 2 , A , B , C )    =>  { Move ( A , C )                {
=> {  Move ( A , C )                    { Hanoi( n - 3 , C , B , A )
   {  Hanoi( n - 2 , B , A , C )

一直往下递归，直到如上所示的.

"(***)" 作为第一句,然后回溯依次执行。

……

对于递归函数的设计，我们需要做到“整体把握”

但对于具体实现的过程，一定要明确其中的“具体过程”。

如果把该程序比做一棵递归树(三叉树)，打印到屏幕的第一句执行的必定是整棵树的最左下角的叶子结点。

对于问题的阐述：（以图作为例子）

f(n) -> f(n-1) + 1 + f(n-1)
f(n-1) -> f(n-2) + 1 + f(n-2)
……
        f(2) -> f(1) + "1" + f(1)
        f(0) + 1 + f(0) + "1" + f(0) + 1 + f(0)
              ---
         第一个执行的操作

切面条

一根高筋拉面，中间切一刀，可以得到2根面条。
如果先对折1次，中间切一刀，可以得到3根面条。
如果连续对折2次，中间切一刀，可以得到5根面条。
那么，连续对折10次，中间切一刀，会得到多少面条呢？

题目提及到了“对折”一词。

必定是会使面条加倍
f(0) = 2
f(1) = 3
f(2) = 5
f(3) = 9
f(4) = 17
……
肯定是围绕着幂次进行找规律。
所以答案就是f(n) = 2^n + 1

补充的内容，并不是考点。

快速幂

算法步骤如上所示：

其实仅仅是利用任何数字转变成2进制后，

每一个位置上权值要么为‘1’，要么为‘0’的特点。

我们可以通过基数和指数相互配合，基数和底数同时进行左移。

若当前指数所对应的位置是'1'

ans 必须乘以当前底数

若当前指数所对应的位置为'0'

不执行任何操作

若指数所对应的位置越界时则算法结束，当前对应的ans=pow( base , n )

 1 #include<iostream>
 2 using namespace std;
 3 
 4 //快速幂函数
 5 int qpow( int a , int b ){
 6     int ans = 1 ;
 7     //把目标次幂b ->转化成2进制.
 8     while( b ){
 9         //如果当前是b最末尾为1答案进行累成
10         if( b % 2 == 1 ){
11             ans = ans * a ;
12         }
13         //基数和次幂同时移位
14         b = b / 2 ;
15         a = a * a ;
16     }
17     //输出答案
18     return ans ;
19 }
20 int main()
21 {
22     int n = 10 , Base = 2;
23     cout << qpow( Base , n ) + 1 << endl ;
24     return 0;
25 }

快速幂

平面上的直线

【题意】
      平面上有 n 条直线，最多可以把整个平面分成多少份？

L(0) = 1
L(1) = 2
L(2) = 4
L(3) = 7

通过观察可以得知：

L(n) = L(n-1) + n

= L(n-2) + n-1 + n

= ……

= 1 + $Sn$

排列问题

给定 n 个元素，求出这 n 个元素的全排列。

 1 //排列问题
 2 #include<cstdio>
 3 #include<algorithm>
 4 using namespace std;
 5 const int N = 20 ;
 6 int a[N] ;
 7 void Perm( int S , int E ){
 8     if( S == E ){
 9         for( int i = 1 ; i <= E ; i++ ){
10             printf("%3d",a[i]);
11         }
12         putchar('
');
13         return ;
14     }
15     for( int i = S ; i <= E ; i++ ){
16         swap( a[S] , a[i] );
17         Perm( S + 1 , E );
18         swap( a[S] , a[i] );
19     }
20 }
21 int main()
22 {
23     int n = 3 ;
24     for( int i = 1 ; i <=n ; i++ )  a[i] = i ;
25     Perm( 1 , n );
26     return 0 ;
27 }

排列问题

整数划分问题

【题目描述】

将正整数 n 划分为一系列正整数的和：

6=6 6=5+1 6=4+2=4+1+1 6=3+3=3+2+1=3+1+1+1 6=2+2+2=2+2+1+1=2+1+1+1+1 6=1+1+1+1+1+1+1

共11 种情况

书本P14页有具体的推导过程及解释

 1 //整数划分问题 - 公式法
 2 #include<cstdio>
 3 #include<algorithm>
 4 using namespace std;
 5 int solve( int n , int m ){
 6     if( ( n < 1 ) || ( m < 1 ) )
 7         return 0 ;
 8     else if( ( n==1) || ( m==1) )
 9         return 1 ;
10     else if( n < m )
11         return solve( n , n );
12     else if( n == m )
13         return solve( n , m-1 ) + 1 ;
14     else
15         return solve( n , m - 1 ) + solve( n - m , m );
16 }
17 int main()
18 {
19     printf("%d
",solve(6,6));
20     return 0 ;
21 }

整数划分-公式法

模拟多项式乘法即可。

具体原理：https://blog.csdn.net/Z_sea/article/details/86529635

 1 //整数划分-母函数
 2 #include<cstdio>
 3 using namespace std;
 4 const int N = 1e3 + 10 ;
 5 int f[N] , tmp[N] ;
 6 int main()
 7 {
 8     int n = 6 ;
 9     f[0] = 1 ;
10     for( int i = 1 ; i <= n ; i ++ ){
11         for( int j = 0 ; j <= n ; j ++ ){
12             for( int k = i ; k <= n ; k += i ){
13                 tmp[j+k] += f[j] ;
14             }
15         }
16         for( int j = 0 ; j <= n ; j++ ){
17             f[j] += tmp[j] ;
18             tmp[j] = 0 ;
19         }
20     }
21     printf("%d
",f[n]);
22     return 0 ;
23 }

整数划分-母函数

二分搜索技术

【题目描述】

给定已排好序的 n 个元素 a[0:n-1]，在其中查找一个特定元素 x。

 1 #include<cstdio>
 2 using namespace std;
 3 const int N = 1e3 ;
 4 int a[N] = { 1 , 2 , 3 , 6 , 7 , 11 };
 5 int main()
 6 {
 7     int x ;
 8     bool flag = false ;
 9     scanf("%d",&x);
10     int L = 0 , R = 6 ;
11     while( L <= R ){
12         int Mid = ( L + R ) / 2 ;
13         if( a[Mid] == x ){
14             printf("Index : %d
",Mid);
15             flag = true ;
16         }
17 
18         if( x < a[Mid] ) R = Mid - 1 ;
19         else L = Mid + 1 ;
20     }
21     if( !flag ){
22         printf("Not Found
");
23     }
24     return 0 ;
25 }
26 /*
27 1
28 Index : 0
29 
30 10
31 Not Found
32 */

二分搜索

棋盘覆盖

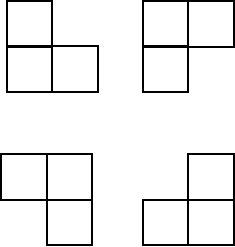
【分析】

分四个部分，如果是特殊点标注的部分，则另外3个部分的顶角位置标注，再进行分治。

最后问题会一直标记，问题规模不断减少，直到为一个格子时则返回。

【具体代码】

 1 //棋盘覆盖
 2 #include<cstdio>
 3 const int N = 8 ;
 4 //t(x,y) -> top-left :左上角的坐标
 5 //s(x,y) -> special  :特殊标识的坐标
 6 //L     :   讨论当前方格的边长
 7 //tag   :   时间戳
 8 int chessboard[N][N] ;
 9 int tag = 1 ;
10 void f( int tx , int ty , int sx , int sy , int L ){
11 
12     if( L == 1 ){
13         return ;
14     }
15     int t = tag ++ ;
16     int len = L / 2 ;
17 
18     //判断特殊点是否在左上部分?
19     if( sx < tx + len && sy < ty + len ){
20         //继续分治
21         f( tx , ty , sx , sy , len );
22     }else{
23         //填上序号,并继续分治
24         chessboard[tx+len-1][ty+len-1] = t ;
25         f( tx , ty , tx+len-1 , ty+len-1 , len );
26     }
27 
28     //判断特殊点是否在右上部分?
29     if( sx < tx + len &&  ty + len <= sy ){
30         //继续分治
31         f( tx , ty + len , sx , sy , len );
32     }else{
33         //填上序号,并继续分治
34         chessboard[tx+len-1][ty+len] = t ;
35         f( tx , ty + len , tx+len-1, ty+len , len );
36     }
37 
38     //判断特殊点是否在左下部分?
39     if( tx + len <= sx && sy < ty + len ){
40         //继续分治
41         f( tx + len , ty , sx , sy , len );
42     }else{
43         //填上序号,并继续分治
44         chessboard[tx+len][ty+len-1] = t ;
45         f( tx + len , ty , tx+len , ty+len-1 , len );
46     }
47 
48     //判断特殊点是否在右下部分?
49     if( tx + len <= sx && ty + len <= sy ){
50         //继续分治
51         f( tx + len , ty + len , sx , sy , len );
52     }else{
53         //填上序号,并继续分治
54         chessboard[tx+len][ty+len] = t ;
55         f( tx + len , ty + len , tx+len , ty+len , len );
56     }
57 
58 
59 }
60 int main()
61 {
62     //棋盘初始左上角,初始特殊点,边长为8
63     f( 0 , 0 , 0 , 1 , 8 );
64     for( int i = 0 ; i < 8 ; i++ ){
65         for( int j = 0 ; j < 8 ; j++ ){
66             printf("%4d",chessboard[i][j]);
67         }
68         putchar('
');
69     }
70     return 0 ;
71 }

棋盘覆盖