【主要内容】
动态规划
背包类型的dp:01背包
线性dp:最长公共子序列,编辑距离
经典例题: 独立任务最优调度,最大子段和
01背包
【题目链接】
https://www.acwing.com/problem/content/2/
【题目描述】
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。 输出最大价值。
【数据范围】
0<N,V≤1000 0<vi,wi≤1000
【输入样例】
4 5
1 2
2 4
3 4
4 5
【输出样例】
8
【题解】 设 f[i][j]挑选前i个物品放入背包在容量为j时,获取的最大价值。
在挑选第i个物品时,当能放入的情况下,写出对应的状态转移方程:
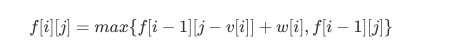
即放入时,腾出对应的空间出来放物品,同时获取对应的价值。
最后相比较,在放与不放之间取最大值

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 const int N = 1e3 + 10 ; 5 int f[N][N] , v[N] , w[N] ; 6 int main() 7 { 8 int n , V ; 9 scanf("%d%d",&n,&V); 10 for( int i = 1 ; i <= n ; i++ ){ 11 scanf("%d%d",&v[i],&w[i]); 12 } 13 14 //枚举物品 15 for( int i = 1 ; i <= n ; i++ ){ 16 //枚举背包容量 17 for( int j = 0 ; j <= V ; j ++ ){ 18 //如果能承载该物品,基于前i-1个物品的情况后放入,若能比不放 的价值大则替换 19 if( j >= v[i] ){ 20 f[i][j] = max( f[i-1][j] , f[i-1][j-v[i]] + w[i] ); 21 } 22 //若不能放入,则维持原来的价值. 23 else{ 24 f[i][j] = f[i-1][j] ; 25 } 26 } 27 } 28 printf("%d ",f[n][V]); 29 return 0; 30 }
最长公共子序列
【题目链接】
https://www.acwing.com/problem/content/899/
【题目描述】
给定两个长度分别为N和M的字符串A和B,求既是A的子序列又是B的子序列的字符串长度最长是多少。
【数据范围】
1≤N≤1000
【输入样例】
4 5
acbd
abedc
【输出样例】
3
【题解】
对于字符串ABCDE BD是其中一个子序列
设f[ i ][ j ] 为A串前i个字符与B串前j个字符 两者构成最长的子序列 的 长度。
状态转移方程为:
当两个字符相同时

否则
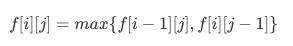
其含义为:
在匹配第i个和第j个相符时,我们可以把问题转移到
否则,问题抛给 f( i - 1 , j ) , f( i , j - 1 )
【具体代码】

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 const int N = 1e3+10 ; 5 char A[N] , B[N] ; 6 int f[N][N] ; 7 int main() 8 { 9 int n , m ; 10 scanf("%d%d%s%s",&n,&m,A+1,B+1); 11 for( int i = 1 ; i <= n ; i++ ){ 12 for( int j = 1 ; j <= m ; j ++ ){ 13 if( A[i] == B[j] ){ 14 f[i][j] = f[i-1][j-1] + 1 ; 15 }else{ 16 f[i][j] = max( f[i-1][j] , f[i][j-1] ); 17 } 18 } 19 } 20 printf("%d ",f[n][m]); 21 return 0 ; 22 }
编辑距离
【题目链接】
https://www.acwing.com/problem/content/904/
【题目描述】
给定两个字符串A和B,现在要将A经过若干操作变为B,可进行的操作有:
-
删除–将字符串A中的某个字符删除。
-
插入–在字符串A的某个位置插入某个字符。
-
替换–将字符串A中的某个字符替换为另一个字符。
现在请你求出,将A变为B至少需要进行多少次操作。
【数据范围】
1≤n,m≤1000
【输入样例】
10
AGTCTGACGC
11
AGTAAGTAGGC
【输出样例】
4
【题解】
设 f[i][j] 为A串前i个字符通过编辑变成B串中前j个字符 所需要最少的操作步数。
编辑有三种操作,对应着三种情况。
A串前i个字符编辑成B串前j个字符。
增加一个字符:
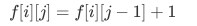
删除一个字符:
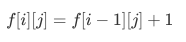
修改一个字符:
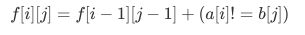
f[ i ] [ j ] 就是以上三种情况取最小值即可。
【具体代码】

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 const int N = 1e3 + 10 ; 6 char A[N],B[N] ; 7 int f[N][N] ; 8 int main(){ 9 int n , m ; 10 scanf("%d%s%d%s",&n,A+1,&m,B+1); 11 12 memset( f , 0x3f , sizeof f ); 13 for( int i = 0 ; i <= n ; i++ ) f[i][0] = i ; 14 for( int j = 0 ; j <= m ; j++ ) f[0][j] = j ; 15 16 for( int i = 1 ; i <= n ; i++ ){ 17 for( int j = 1 ; j <= m ; j++ ){ 18 f[i][j] = min( min( f[i-1][j] + 1 , f[i][j-1] + 1 ) , f[i-1][j-1] + ( A[i] != B[j] ) ); 19 } 20 } 21 printf("%d ",f[n][m]); 22 return 0 ; 23 }
最大子段和
【题目链接】
https://leetcode-cn.com/problems/maximum-subarray
【题目描述】
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4], 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
【题解】
最大字段和,其字段是“连续”的一段,不是片段。
因为给定的一系列数里面可能有负数。
[-1,2,3,-6,7]序列中最大子段和值为7。
从左往右看,我们肯定是从一个正数开始的,[2,3]=5,但是遇到-6后发现不能继续延伸了,因为此时已经累计和为-1,如果是继承前面的累加和,而是直接从自己开始,所以是7.
根据上述分析后,我们直接定义
f[i] 为前i个数字最大子段和。
答案就是过程中找到。

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 const int N = 1e4 + 10 ; 5 int n ; 6 int a[N] ; 7 int f[N] ; 8 int res = -0x3f3f3f3f ; 9 int main() 10 { 11 scanf("%d",&n); 12 for( int i = 1 ; i <= n ; i++ ){ 13 scanf("%d",&a[i]); 14 } 15 for( int i = 1 ; i <= n ; i++ ){ 16 //从左边累加过来或者从当前位置开始 17 f[i] = max( f[i-1] , 0 ) + a[i] ; 18 res = max( res , f[i] ) ; 19 } 20 /* 21 for( int i = 1 ; i <= n ; i++ ){ 22 printf("%3d",f[i]); 23 } 24 puts(""); 25 */ 26 printf("%d ",res); 27 return 0; 28 } 29 /* 30 9 31 -2 1 -3 4 -1 2 1 -5 4 32 33 6 34 */
独立任务最优调度
【题目描述】
独立任务最优调度,又称双机调度问题:用两台处理机A和B处理n个作业。设第i个作业交给机器A处理时所需要的时间是a[i],若由机器B来处理,则所需要的时间是b[i]。现在要求每个作业只能由一台机器处理,每台机器都不能同时处理两个作业。设计一个动态规划算法,使得这两台机器处理完这n个作业的时间最短(从任何一台机器开工到最后一台机器停工的总的时间)。研究一个实例:n=6, a = {2, 5, 7, 10, 5, 2}, b = {3, 8, 4, 11, 3, 4}.
【参考博客】
https://www.jianshu.com/p/1e8a1a617c3b
【题解】
其实应该有一个严格的压维过程的,参考博客中已经展示出来了。
我认为可以直接看参考博客,简单易懂。
【个人见解】
完全是个人见解。
问题其实就好比01背包问题。
两台机器的最优调度,第一台机器处理的任务 好比背包里的物品,同时不在背包里的物品则为另外一台机器所处理的任务。
物品的代价是时间,价值也是时间。
背包问题最优解不再是背包里的价值最大,而是放进背包里的总价值,和没有放入背包的物品的总价值 之间取的最大值。
首先要知道这个物品在背包时的价值与不放入背包时的价值不一样。
放入时价值为:a[i] , 没有放入时为:b[i]
如果有一种情况是:放入背包里所有的价值之和A,与其不放入的价值之和B。
答案就是max{A,B}。
但是这仅仅是对于一种情况来说的,
而所有情况中取最小值。
设f[ i ][ j ] 为完成前i个任务在背包为j时,不在背包里物品的总价值。
即j为放入背包中的总价值,而f[i][j]为不放入背包中的总价值。
答案为:Max{ j , f[ i ][ j ] }

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 const int N = 1e3 + 10 ; 5 int f[N][N] ; 6 int a[N] , b[N] ; 7 int n ; 8 int main() 9 { 10 scanf("%d",&n); 11 for( int i = 1 ; i <= n ; i++ ) scanf("%d",&a[i]); 12 for( int i = 1 ; i <= n ; i++ ) scanf("%d",&b[i]); 13 /* 14 memset( f , 0x3f , sizeof f ); 15 for( int i = 0 ; i < a[1] ; i++ ) f[0][i] = 0 ; 16 */ 17 int total_time_A = 0 ; 18 int res = 0x3f3f3f3f ; 19 for( int i = 1 ; i <= n ; i++ ){ 20 total_time_A += a[i] ; 21 for( int j = 0 ; j <= total_time_A ; j++ ){ 22 if( j < a[i] ){ 23 f[i][j] = f[i-1][j] + b[i] ; 24 }else{ 25 f[i][j] = min( f[i-1][j] + b[i] , f[i-1][j-a[i]] ); 26 } 27 if( i == n ) 28 res = min( res , max( f[n][j] , j ) ) ; 29 } 30 } 31 printf("%d ",res); 32 return 0 ; 33 } 34 35 /* 36 6 37 2 5 7 10 5 2 38 3 8 4 11 3 4 39 40 15 41 */
