题目描述
- 给出
- 表示一个的格点图,求能够互相看见的点对个数对取模的值.
- 能互相看见定义为此两点连线上没有其他的格点且欧氏距离在[l,r]范围内
题目分析
-
首先我们将上下左右相邻的点对特判:
当时有个上下左右相邻点对对答案造成贡献 -
此时我们只需要找出某个长宽互质矩形的对角线(两条)能够对答案造成多少贡献即可,如图,在长宽为的矩形中,长宽为的子矩形的副对角线对答案造成了的贡献:
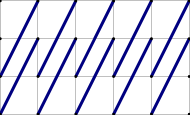
所以在求某个矩形造成的总贡献时就用一条对角线的贡献乘以即可
由于可以求
所以枚举,枚举d即可
总时间复杂度
Tips
- 此处还有[l,r]的限制,首先考虑[1,k]怎么做
只用满足即可
则
- 对于,答案就是
此处不能用与作为参数代进去,因为两点距离的值域为,不一定为整数,会多减一部分答案
AC code
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXN = 100005;
int n, m, mod, l, r, ans;
int Prime[MAXN], Cnt, mu[MAXN];
bool IsnotPrime[MAXN];
void init()
{
mu[1] = 1;
for(int i = 2; i < MAXN; ++i)
{
if(!IsnotPrime[i])
Prime[++Cnt] = i, mu[i] = -1;
for(int j = 1; j <= Cnt && Prime[j] * i < MAXN; ++j)
{
IsnotPrime[Prime[j] * i] = 1;
if(i % Prime[j] == 0)
{
mu[Prime[j] * i] = 0;
break;
}
mu[Prime[j] * i] = -mu[i];
}
}
}
inline int F(int k, int d)
{
return (1ll * k * (m+1) % mod - 1ll * d * ((1ll*k*(k+1)/2) % mod) % mod) % mod;
}
inline int solve(long long k) // y*y <= k*k - x*x
{
int ret = 0;
for(int x = 1; x <= n && 1ll*x*x < k; ++x)
{
int s = 0, up = min(m, int(sqrt(1.0*k-1.0*x*x)));
for(int d = 1, d2; d*d <= x; ++d) if(x % d == 0)
{
s = (s + 1ll * mu[d] * F(up/d, d) % mod) % mod;
if(d != (d2=x/d))
s = (s + 1ll * mu[d2] * F(up/d2, d2) % mod) % mod;
}
ret = (ret + 1ll * s * (n+1-x) % mod) % mod;
}
return 2ll * ret % mod;
}
int main ()
{
scanf("%d%d%d%d%d", &n, &m, &l, &r, &mod); init();
int Ans = ((solve(1ll*r*r)-solve(1ll*l*l-1)) % mod + mod) % mod;
if(l <= 1 && 1 <= r) Ans = (Ans + ((2ll * n * m % mod + n) % mod + m) % mod) % mod;
printf("%d
", Ans);
}