题目大意
给定一个$3 imes N$的方阵,每个位置的数恰好是每一个$[1,3 imes N]$中的数。
初始时,每个位置$[x,y]$填的是$3(y-1)+x,(1leq xleq N,1leq yleq 3)$
例如$N=5$时如下图
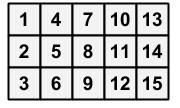
现在给定一个尺寸完全相同的方阵,可以进行任意次此操作:
选择方阵中一个$3 imes 3$的方阵,将这个方阵绕着中心点旋转$180°$
问是否有一种合法操作,使得初始状态成为给定的方阵。
题解:
考虑构造
首先我们可以排除任意$3x+1,3x+2,3x+3$没有按照顺序排在一列的情况,
随后对于每一列,有意义的只有它初始状态的位置和其上下的方向。
再考上并没有一次看透题目,凭借平时拧模仿的经验,可以先转转试试看。
既然想完成高端操作,就要从复杂的转法入手。
用字母表示每一列的位置,大写表示从上到下降序,小写表示从上到下升序。
有$aspace bspace cspace d ightarrow Cspace Bspace Aspace d ightarrow Cspace Dspace aspace b ightarrow Aspace dspace cspace b ightarrow Aspace Bspace Cspace D$
即,对于任意连续四列,我们可以将每一列方向取反,且位置不变。
另有$aspace bspace cspace dspace e ightarrow Cspace Bspace Aspace dspace espace ightarrow Cspace Bspace Espace Dspace a ightarrow espace bspace cspace Dspace a ightarrow espace bspace Aspace dspace C ightarrow aspace Bspace Espace dspace C ightarrow aspace Bspace cspace Dspace e$
即,对于任意连续五列,我们可以将第二、四列取反同时保持顺序不变。
两者综合一下,就可以转化为对于连续五个,我们可以将其中两个相隔$1$列的列的方向取反,其余顺序不变。
现在我们只需要解决如何快速简洁地将每一列转回原来的位置上即可。
按每列地初始位置从小到大地顺序考虑,将每一列从右向左转回原来的位置:
假设有$xbcdefgha$,我们欲将$a$转回$x$,若要移动的距离不是$2$的倍数,则无解。
否则 ,我们希望改动最小,先不可避免地将$a$转到$x$的位置,就有$aBXDCFEHG$,但是我们发现这样改动的太多了,但不难发现,只要把$X$再转回$a$原来的位置,就可以得到$aBcdefghx$,这样,一共就交换了$a$,$x$的位置,同时改变了$x$右一列的方向。
特别的,如果$a$,$x$距离列数是$2$的倍数但不是$4$的倍数,则涉及$a$和$x$的操作有奇数次,$a$和$x$均要变向。
所以,我们首先要把每一列转到它所在的位置,然后在$nleq 4$时特判,其余情况从小到大枚举位置$i$,如果第$i$列不是从上到下升序,就将第$i$和第$i+2$列变向,若第$n-1$和第$n$位最终至少有一位不满足从上到下升序,则无解,否则我们已经构造出了合法可行解。
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#define LL long long
#define M 500020
using namespace std;
int read(){
int nm=0,fh=1;char cw=getchar();
for(;!isdigit(cw);cw=getchar()) if(cw=='-') fh=-fh;
for(;isdigit(cw);cw=getchar()) nm=nm*10+(cw-'0');
return nm*fh;
}
int n,m,t[3][M],p[M],cnt,pos[M];
void fail(){puts("No");exit(0);}
void ROW(int x,int y,int z){
if(x>z) swap(x,z);
if(y!=x+1||y!=z-1) return fail();
if(y%3!=2) return fail();
}
int main(){
n=read();
for(int j=0;j<3;j++){
for(int i=1;i<=n;i++) t[j][i]=read();
}
for(int i=1;i<=n;i++){
ROW(t[0][i],t[1][i],t[2][i]);
p[i]=(t[1][i]+1)/3;
if(t[0][i]>t[2][i]) p[i]=-p[i];
if(abs(abs(p[i])-i)&1) fail();
pos[abs(p[i])]=i;
}
for(int i=1;i<=n;i++){
if(pos[i]==i) continue;
p[i+1]=-p[i+1],swap(p[i],p[pos[i]]);
if((abs(i-pos[i])>>1)&1) p[i]=-p[i],p[pos[i]]=-p[pos[i]];
pos[abs(p[pos[i]])]=pos[i],pos[i]=i;
}
for(int i=1;i<=n;i++) if(p[i]<0) cnt++;
if(cnt&1) fail();
if(n<=3&&cnt>0) fail();
if(n==4&&cnt%4>0) fail();
for(int i=1;i<n-1;i++) if(p[i]<0) p[i]=-p[i],p[i+2]=-p[i+2];
if(p[n-1]<0||p[n]<0) fail();
puts("Yes");
return 0;
}