信息量的直观描述:
概率很大,受试者事前对事件有估计,所以信息量小;反之,概率很小,受试者对事件感到突然,所以信息量大。
信息量的定义:
一个消息$x$出现的概率是$p$,那么它的信息量为:$$I=-log(p)$$
这也符合信息量关于概率$p$单减的直观感受。底数为2(单位为bit),或者为e(单位nat),或者为10(单位hart)。
信息熵的定义:
一个信源的信息量,即该信源所有可能发出的消息的平均不确定性:$$H(X)=sum p(x_i)I(x_i)=-sum p(x_i) log(p(x_i))$$
单个信源的信息熵举例:
- 一枚硬币抛正面、抛反面的概率均是$frac{1}{2}$,问抛一枚硬币的信息熵是多少?
- 一枚硬币抛正面的概率是$frac{1}{4}$,抛反面的概率是$frac{3}{4}$,问抛一枚硬币的信息熵是多少?
from math import log import numpy as np A1=np.array([1/2,1/2]) A2=np.array([1/4,3/4]) H1,H2=0,0 for p in A1: if p>0: H1+=-p*log(p,2) for p in A2: if p>0: H2+=-p*log(p,2) print('H1=',H1,'H2=',H2)
>> H1= 1.0 H2= 0.8112781244591328
这个有意思:材质均匀的硬币的信息熵 > 材质不均匀的硬币的信息熵,也就是不均匀的硬币的不确定性减少了,由此也解释了出老千。
条件熵:
度量了在已知事件Y发生的情况下,事件X发生的不确定性:$$H(X|Y)=sum p(y_j)H(X|y_j)=-sum p(y_i) log(p(x_i|y_i))$$
条件熵举例:
事件X:进行或取消户外活动;事件Y:天气情况(晴、阴、雨)
求:在已知天气情况的情况下,活动是否进行的条件熵

解:p(Y='晴')=$frac{5}{14}$,p(Y='阴')=$frac{4}{14}$,p(Y='雨')=$frac{5}{14}$
在已知Y情况下的条件概率分布汇总:(注意:不是联合概率分布)
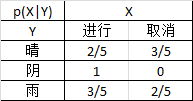
H(X|Y='晴')=-p(X='进行'|Y='晴')log(p(X='进行'|Y='晴')) - p(X='取消'|Y='晴'))log(p(X='取消'|Y='晴'))
=$-frac{2}{5} imes log(frac{2}{5}) - frac{3}{5} imes log(frac{3}{5}) $
=0.971
同样可求H(X|Y='阴')=$0$,H(X|Y='雨')=0.971
所以,H(X|Y)=p(Y='晴')H(X|Y='晴')+p(Y='阴')H(X|Y='阴')+p(Y='雨')H(X|Y='雨')
=$frac{5}{14} imes$ 0.971+$frac{4}{14} imes$ 0 +$frac{5}{14} imes$ 0.971
=0.693
from math import log import numpy as np A1=np.array([5/14,4/14,5/14]) con1=np.array([2/5,3/5]) con2=np.array([1,0]) con3=np.array([3/5,2/5]) H1,H2,H3=0,0,0 for p in con1: if p>0:H1+=-p*log(p,2) for p in con2: if p>0:H2+=-p*log(p,2) for p in con3: if p>0:H3+=-p*log(p,2) H=np.array([H1,H2,H3]) H=np.matmul(A1,H) print('H=',H)
>>H= 0.6935361388961918
信息增益$I(X,Y)=H(X)-H(X|Y)$:
度量了在知道Y后,X的不确定性的减少程度
信息增益举例:
接上述条件熵的例子,求在知道天气情况后,活动的不确定性的减少程度。
解:p(X='进行')=$frac{9}{14}$,p(X='取消')=$frac{5}{14}$
H(X)=-p(X='进行')log(p(X='进行')) - p(X='取消'))log(p(X='取消'))
=$-frac{9}{14} imes log(frac{9}{14}) - frac{5}{14} imes log(frac{5}{14})$
=0.940
所以,信息增益I(X,Y)=H(X)-H(X|Y)=0.940-0.693=0.246
推广到一般的情况:X是数据集(以下记为D),Y作为X分类的一个特征(属性)(以下记为A)。那么也就是根据特征A去分类D,A有3个离散值,A1='晴',A2='阴',A3='雨',标记D的类别为实例数最多的类别。若没有其他特征,那么当A1='晴'时,有2天活动取消,3天活动进行,则D标记为'取消';A2='阴'时,4天全是活动进行,则D标记为'进行';A3='雨'时,同理标记为'进行'。这显然不符合常识,因为事实上还有其他因素决定是否进行户外活动,比如温度、风速等其他特征。
ID3就是用来决定选取特征的先后顺序,该顺序需要有一个定量的标准。
ID3:用信息增量最大的特征作为决策树当前的结点
1. 在所有特征A1,A2,...,An中,找出信息增量最大的特征作为根结点,比如Ak
2. 以Ak的所有取值类别作为分支
3. 若该分支中所有D的分类结果相同,则作为叶子结点结束
4. 否则,继续根据其他特征递归划分
ID3举例:有如下数据集,共14个样本,4个特征(天气、温度、湿度、风俗),求生成一棵能判别是否进行活动的决策树。
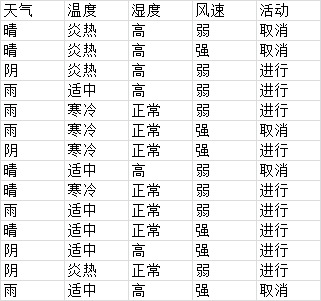
代码解决待续
ID3算法的4大缺点: 改进C4.5
1. 无法处理连续特征 --> 连续特征离散化
2. 取值类别多的特征比取值类别少的特征的信息增益大 --> 信息增益比
比如特征A1有两个取值,概率各为$frac{1}{2}$;特征A2有三个取值,概率各为$frac{1}{3}$,本应不确定性相同,但是A2的信息增量比A1的信息增量大
直观感受是特征类别多,每个类别的样本数变少,样本更容易被划分到散落的各个类别,即样本的不确定性变小。
3. 没有考虑缺失值情况 --> 设置权重
4. 易于过拟合 --> 正则化
参考1:刘建平Pinard的博文内容 https://www.cnblogs.com/pinard/p/6050306.html
参考2:ID3算法的实例分析 https://wenku.baidu.com/view/9bf8646f172ded630b1cb6c1.html
代码参考1:ID3算法的Python实现 https://www.xuebuyuan.com/3191192.html