主讲人 网络上的尼采
(新浪微博: @Nietzsche_复杂网络机器学习)
网络上的尼采(813394698) 9:11:56
开始吧,先不要发言了,先讲PRML第二章Probability Distributions。今天的内容比较多,还是边思考边打字,会比较慢,大家不要着急,上午讲不完下午会接着讲。
顾名思义,PRML第二章Probability Distributions的主要内容有:伯努利分布、 二项式 –beta共轭分布、多项式分布 -狄利克雷共轭分布 、高斯分布 、频率派和贝叶斯派的区别联系 、指数族等。
先看最简单的伯努利分布:
最简单的例子就是抛硬币,正反面的概率。
再看二项式分布: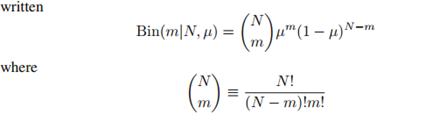
抛N次有m次是正面或反面的概率,所以伯努利分布是二项式分布的特例。
向大家推荐一本好书,陈希孺的《数理统计简史》,对数理统计的一些基本东西的来龙去脉介绍的很详细,这样有助于理解。先818二项式分布,正态分布被发现前,二项式分布是大家研究的主要内容。
由二项式分布可以推出其他很多分布形式,比如泊松定理:
泊松分布是二项式分布的极限形式,这个估计大家都推导过。由二项式分布也能推出正态分布。
贝叶斯思想也是当时对二项式分布做估计产生的,后来沉寂了一百多年。
数据少时用最大似然方法估计参数会过拟合,而贝叶斯方法认为模型参数有一个先验分布,因此共轭分布在贝叶斯方法中很重要,现在看二项式分布的共轭分布beta分布:
结合上面的二项式分布的形式,不难看出beta分布和二项式分布的似然函数有着相同的形式,这样用beta分布做二项式分布参数的先验分布,乘似然函数以后得到的后验分布依然是beta分布。
a b是超参,大家可以看到beta分布的形式非常灵活:
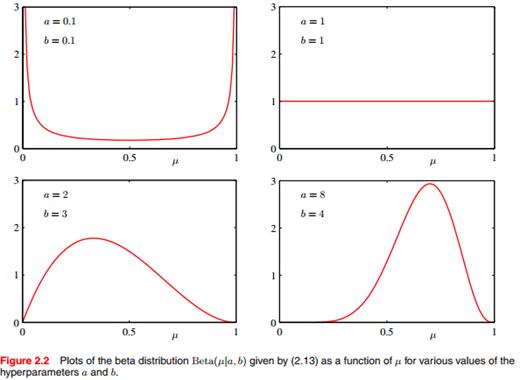
假设抛硬币N次,l和m分别为正反面的记数,那么参数的后验分布便是:
不难看出,后验分布是先验和数据共同作用的结果。
这种数据矫正先验的形式可以通过序列的形式进行,非常适合在线学习。
单拿一步来说明问题: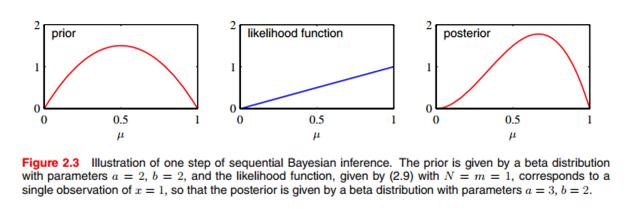
可以看出,a的记数增加了1。
书上通过序列数据流的形式来矫正先验的描述,每次可以用一个观测数据也可以用small batches,很适合实时的学习:
回到上面的二项式-beta共轭,随着数据的增加,m,l趋于无穷大时,这时参数的后验分布就等于最大似然解。
有些先验分布可以证明,随着数据的增加方差越来越小,分布越来越陡,最后坍缩成狄拉克函数,这时贝叶斯方法和频率派方法是等价的。举个第三章的贝叶斯线性回归的例子,对于下图中间参数W的高斯先验分布,随着数据不断增加,参数后验分布的不确定性逐渐减少,朝一个点坍缩:
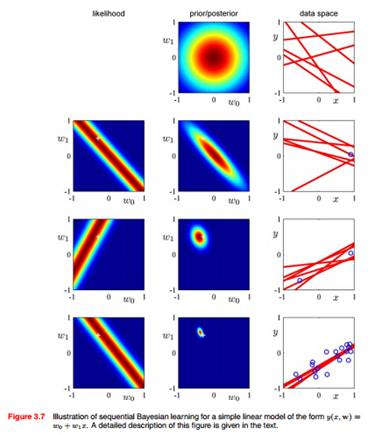
接着看多项式分布:把抛硬币换成了掷骰子
同样它的共轭分布狄利克雷分布也得和似然函数保持相同的形式。
狄利克雷分布:

后验形式:

大家依然能看到记数。
下面讲高斯分布,大家看高斯分布的形式:
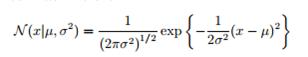
多元高斯分布的形式:

高斯分布有着优良的性质 ,便于推导,很多时候会得到解析解。一元高斯分布是个钟形的曲线,大部分都集中在均值附近,朝两边的概率呈指数衰减,这个可以用契比雪夫不等式来说明,偏离均值超过3个标准差的概率就非常低了:

正态分布是如何发现的,在《数理统计简史》有详细的介绍,当时已经有很多人包括拉普拉斯在找随机误差的分布形式,都没有找到,高斯是出于一个假设找到的,也就是随机误差分布的最大似然解是算数平均值,只有正态分布这个函数满足这个要求。
然后高斯进一步将随机误差的正态分布假设和最小二乘联系到了一块,两者是等价的:

后来就是拉普拉斯迅速跟进,提出了中心极限定理,大量随机变量的和呈正态分布,这样解释了随机误差是正态分布的原因。中心极限定理的公式:

大家看PRML上的图,很形象的说明高斯分布是怎么生长出来的: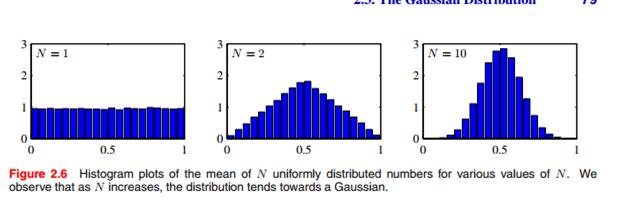
从[0,1]随机取N个变量,然后算它们的算术平均,随着N的增大,均值的分布逐渐呈现出高斯分布,可以比较直观的了解中心极限定理 。
接着看高斯分布的几何形式:
先给出样本到均值的马氏距离
把协方差矩阵的逆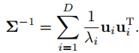 带入上式
带入上式
会得到以协方差矩阵的特征值平方根为轴长的标准椭圆方程
其中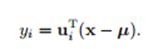
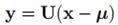 ,也就是原来的坐标系经过平移和旋转,由协方差矩阵特征向量组成的矩阵U负责旋转坐标轴。
,也就是原来的坐标系经过平移和旋转,由协方差矩阵特征向量组成的矩阵U负责旋转坐标轴。
看下面张图就很明白了:
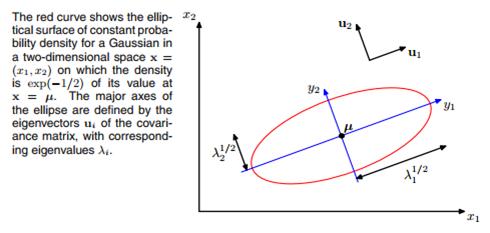
接着是条件高斯分布和边缘高斯分布,这两个分布由高斯分布组成,自身也是高斯分布。
条件高斯分布的推导过程略过,大家记住这个结论: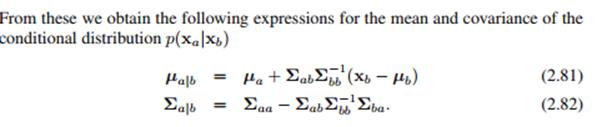
上面是条件高斯分布的均值和方差,以后的Gaussian Processes在最后预测时会用到均值。
另一个是线性高斯模型 p(y|x)均值是 x 的线性函数,协方差与 x 独立,也会经常用到。
接下来是关于高斯分布的贝叶斯方法,方差已知均值未知,先验用高斯分布;均值已知方差未知用Gamma分布;都不知道用Gaussian-Gamma distribution。这方面的推导略过,大家用到时翻书查看就行了:

接下来看Student t-distribution,Student是笔名,此人在数理统计史上是非常nb的人物。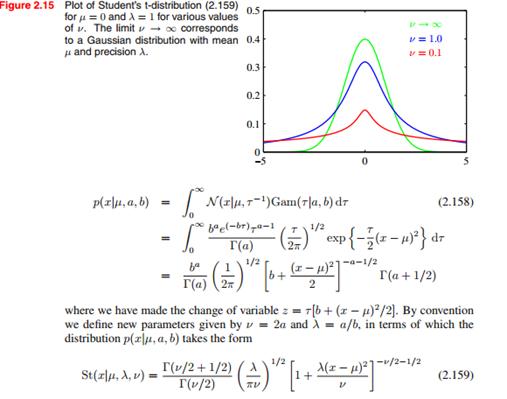
上面是t分布的形式,具体如何发现的可以参看《数理统计简史》,大家看上面的积分形式,t分布其实是无限个均值一样,方差不同的高斯分布混合而成,高斯分布是它的特例,相比较高斯分布,t分布对outliers干扰的鲁棒性要强很多。
从这个图就可以看出,高斯分布对右边孤立点的干扰很敏感,t分布基本上没有变化:
接着讲混合高斯分布:看下图里的例子,单个高斯分布表达能力有限,无法捕捉到两个簇结构:
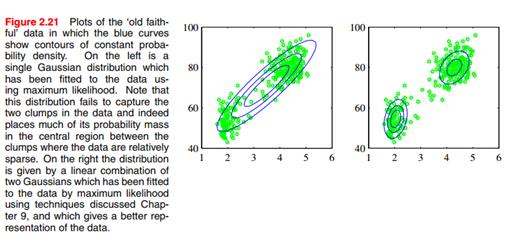
我们可以多个高斯分布的线性组合来逼近复杂的分布,并且对非指数族的分布也一样有效。
混合高斯分布的形式:
RIVERS(773600590) 11:01:09
可不可以使用非线性的组合呢?
网络上的尼采(813394698) 11:01:48
那就太复杂了 这个图是三个高斯分布混合逼近一个复杂分布的例子。
这个图是三个高斯分布混合逼近一个复杂分布的例子。
混合高斯模型里面有一个隐变量,也就是数据点属于哪个高斯分布。
这个就是隐变量的期望:
这个是我们的最大似然目标函数:
可以用EM算法,一边是隐变量,一边是模型的参数,迭代着来回倒腾,收敛到局部最优。混合高斯我在第九章详细讲了,感兴趣的可以看下原来的记录。
xunyu(2118773) 11:09:18
隐变量和最大似然函数的联系在哪里
落英缤纷(348609341) 11:10:16
不设置隐变量直接用ML不好解
网络上的尼采(813394698) 11:10:31
下面讲指数族,很多分布包括我们上面提到的二项式分布、beta分布、多项式分布、狄利克雷分布、高斯分布都可以转换成这种指数族的形式: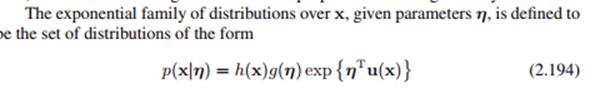
其中η是参数,g(η)是归一化因子,u(x)是x的函数。
指数族的似然函数: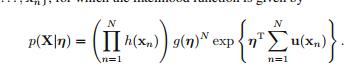
对lnp(X|η)关于η求导,令其等于0,会得到最大似然解的形式: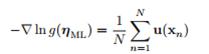
很显然,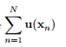 是充分统计量。充分统计量其实很好理解,拿最简单的二项式分布来说,抛硬币我们只需要记住正反面出现的次数就行,原来的数据就可以丢弃了。
是充分统计量。充分统计量其实很好理解,拿最简单的二项式分布来说,抛硬币我们只需要记住正反面出现的次数就行,原来的数据就可以丢弃了。
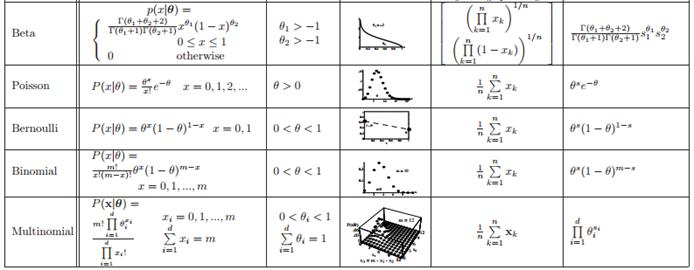
DUDA是指数族专家,这是从他书上截的图,大家可以看下表中的指数族:
 指数族的共轭先验形式:
指数族的共轭先验形式: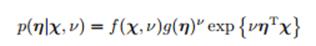
后验形式:
PRML读书会讲稿PDF版本以及更多资源下载地址:http://vdisk.weibo.com/u/1841149974