【纪中受难记】——Day20：祈祷落幕时

再考三天就可以回去了（不过回去也是颓）。

10/0/0

A组题难度真不是盖的，但不排除我弱的可能性。

Description

给定整数 n 和 x，以及一个大小为 n 的序列 a。
你可以选择一个区间 [l,r]，然后令 a[i]+=d(l<=i<=r)，其中 d 满足 |d|<=x。
要求最大化 a 的最长上升子序列的长度，并输出该值
 

Input

第一行输入包含两个整数 n 和 x。
接下来一行 n 个整数表示序列 a。

Output

输出只有一行，包含一个整数，a 的最长上升子序列的最大值。
 

Sample Input

8 10
7 3 5 12 2 7 3 4
 

Sample Output

5
 
 

Data Constraint

对于 5% 的数据点，n,x<=10；
对于另外 10% 的数据点，n,x<=50；
对于另外 13% 的数据点，n<=1000；
对于另外 10% 的数据点，x=0；
对于另外 20% 的数据点，x<=5,n<=50000；
对于另外 17% 的数据点，x=10^9；
对于 100% 的数据点，n<=200000,x<=10^9。

考场上想出写法，但不知道具体怎么搞，最后就打了个最长上升子序列板子，水了10分。

正解：容易发现，如果我们将一个区间[l,r]升高一个值，不如将[l,n]都升高，是等效的，反之同理，所以枚举分割线即可。

这个题解不是我写的，参考自某位大佬，但是还没看懂，先贴在这。

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int N=4e5+10;
 4 int a[N],b[N],c[N],f[N];
 5 int n,d,ans;
 6 struct array{
 7     int arr[N];
 8     void clear(){memset(arr,0,sizeof(arr));}
 9     int lb(int x){return x&-x;}
10     void addl(int x,int y){for(;x<=(n<<1);x+=lb(x))arr[x]=max(arr[x],y);}
11     int queryl(int x){int ans=0;for(;x;x-=lb(x))ans=max(ans,arr[x]);return ans;}
12     void addr(int x,int y){for(;x;x-=lb(x))arr[x]=max(arr[x],y);}
13     int queryr(int x){int ans=0;for(;x<=(n<<1);x+=lb(x))ans=max(ans,arr[x]);return ans;}
14 }t;
15 int main(){
16     freopen("glo.in","r",stdin);
17     freopen("glo.out","w",stdout);
18     scanf("%d%d",&n,&d);
19     for(int i=1;i<=n;i++){
20         scanf("%d",&a[i]);
21         a[i+n]=a[i]+d;
22         b[i]=a[i];
23         b[i+n]=a[i+n];
24     } 
25     sort(b+1,b+n*2+1);
26     int pos=unique(b+1,b+n*2+1)-b-1;
27     for(int i=1;i<=(n<<1);i++){
28         a[i]=lower_bound(b+1,b+pos+1,a[i])-b;
29     }
30     for(int i=1;i<=n;i++){
31         c[i]=t.queryl(a[i+n]-1)+1;
32         f[i]=t.queryl(a[i]-1)+1;
33         t.addl(a[i],f[i]);
34     }
35     t.clear();
36     for(int i=n;i>=1;i--){
37         f[i]=t.queryr(a[i]+1)+1;
38         t.addr(a[i],f[i]);
39     }
40     int ans=0;
41     for(int i=1;i<=n;i++) ans=max(ans,f[i]+c[i]);
42     printf("%d",ans-1);
43     return 0;
44 }

Description

给定一个 r 行 s 列的矩阵，每个格子里都有一个正整数。
问如果从左上角走到右下角，且每次只能向右或向下走到相邻格子，那么使得路径上所有数的乘积不小于 n 的路径有多少条？
由于答案可能很大，所以请输出答案对 10^9+7 取模的结果。
 

Input

第一行三个正整数 r,s,n。
接下来 r 行，每行 s 个正整数，依次表示矩阵每一行的数。

Output

一行一个整数表示答案。
 

Sample Input

Sample 1:
2 3 200
2 3 4
5 6 7

Sample 2:
3 3 90
2 1 1
45 1 1
1 1 1

Sample 3:
2 5 3000
1 2 3 4 5
6 7 8 9 10
 

Sample Output

Sample 1:
2

Sample 2:
3

Sample 3:
3
 

Data Constraint

对于 20% 的数据，矩阵中的数不超过 10；
对于 50% 的数据，1<=r,s<=100；
对于 100% 的数据，1<=r,s<=300,1<=n<=10^6，矩阵中的数不超过10^6。

这题状态很好想，但是有个优化不一定想的到。

首先设f[i][j][k]表示在(i,j)位置时数字乘积为k(k<n)的路径数量，如果这暴力转移，就是O(rsn)，会炸。

那么改变k的意义：k表示数字乘积为x且(n-1)/x=k的方案数。

引入一个概念：

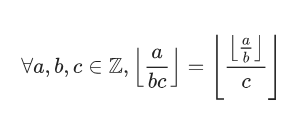
（图源OIWIKI）

这是数论分块，可以保证k的数量级在根号n级别。

由此可以猜想，状态转移是不是可以通过直接除以a[i][j]来实现？

1 for(int i=1;i<=n_;i++){
2     if(idx[cnt]!=n_/i){
3         idx[++cnt]=n_/i;
4         block[n_/i]=cnt;
5     }
6 }

idx[i]表示编号为i的n除去某一个数得到的值，block[i]表示n除去某一个数得到的值的编号是多少。

这样就可以通过枚举编号来求出n除去某个数的情况了。

对于求总路径条数，要用组合数取模来求，可以使用Lucas定理（貌似不用也可以）

没改完，留坑。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=310;
const ll mod=1e9+7;
ll r,s,n_,cnt;
ll a[N][N];
ll f[2][N][5000];
ll block[5000];
ll idx[1000000];
ll jie[1000];
ll quick_p(ll x,ll dd){
    ll res=x,ans=1;
    while(dd){
        if(dd&1) ans=res*ans%mod;
        res=res*res%mod;
        dd>>=1;
    }
    return ans;
}
ll C(ll n,ll m){
    if(m>n) return 0;
    return ((jie[n]*quick_p(jie[m],mod-2))%mod*quick_p(jie[n-m],mod-2)%mod);
}
ll Lucas(ll n,ll m){
    if(!m) return 1;
    return C(n%mod,m%mod)*Lucas(n/mod,m/mod)%mod;
}
int main(){
//    freopen("mobitel.in","r",stdin);
//    freopen("mobitel.out","w",stdout);
    scanf("%lld%lld%lld",&r,&s,&n_);
    n_--;
    jie[0]=1;
    for(int i=1;i<=900;i++){
        jie[i]=(jie[i-1]*i)%mod;
    }
    for(int i=1;i<=r;i++){
        for(int j=1;j<=s;j++){
            scanf("%lld",&a[i][j]);
        }
    }
    for(int i=1;i<=n_;i++){
        if(idx[cnt]!=n_/i){
            idx[++cnt]=n_/i;
            block[n_/i]=cnt;
        }
    }
    f[1][1][1]=1;
    for(int i=1;i<=r;i++){
        int p=i&1;
        for(int j=1;j<=s;j++){
            for(int k=1;k<=cnt;k++){
                f[p][j][block[idx[k]/a[i][j]]]=(f[p][j][block[idx[k]/a[i][j]]]+f[p^1][j][k]+f[p][j-1][k])%mod;
            }
        }
    }
    ll sum=Lucas(r+s-2,s-1);
    for(int i=1;i<=cnt;i++){
        (sum-=f[r&1][s][i])%=mod;
    }
    printf("%lld",(sum+mod)%mod);
    return 0;
}

Description

定义两个序列对应位置上不同的值的个数不超过 k，则可称为 k 相似。
现在有一个长度为 n 的序列 a，将它划分为 n−l+1 个长度为 l 的子串（第 i 个子串为 a[i]~a[i+l-1]）
q 组询问，第 j 组询问给出一个 kj，求每个子串与多少个其它的子串可称为 kj 相似。
 

Input

第一行输入包含两个整数 n 和 l。
接下来一行 n 个整数表示序列 a。
第三行输入一个整数 q。
接下来 q 行每行一个整数 kj。

Output

输出有 q 行，每行 n-l+1 个整数，第 i 个整数表示第 i 个子串与多少个其它的子串可称为 kj 相似。
 

Sample Input

6 2
1 2 1 3 2 1
2
1
2
 

Sample Output

2 1 1 1 1
4 4 4 4 4
 

Data Constraint

对于 25% 的数据点，n<=300；
对于另外 20% 的数据点，n<=2000；
对于另外 20% 的数据点，q=1,k1=1；
对于另外 15% 的数据点，q=1；
对于 100% 的数据点，kj<=l<=n<=10000,q<=100,ai<=10^9。

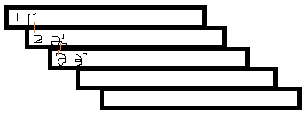
 如图，我们将序列这样重叠摆放，按照距离相同来匹配，发现(1->2),(2->3)的匹配关系，但是当我们匹配到(1`->2`)时，其实可以直接调用(2->3)的答案，减少重复匹配，降低时间复杂度。

实际上我也不会写这道题，尽量解释一下吧。

可以看看这位神仙的题解：https://www.cnblogs.com/AKMer/p/9641894.html

分成几个部分：

1.对询问的处理：

　　首先对于询问集合p[i]，用一个数组存下不同匹配数的询问是否存在。

　　明显，假如有一个答案为k，那么它会对所有大于等于k的匹配做出贡献，这样就可以前缀和处理。

2.对序列的暴力拆分和求解：

　　根据图片可以知道，我们预先求出均等步长的几个串的匹配，就可以直接得到剩下的匹配，因此可以分开来做。

　　(看了我的标程就会知道我是hash了这位神仙的，在此对作者表示歉意)

垃圾jzoj，总是评不过

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int N=1e4+10;
 4 int n,l,d;
 5 int a[N],ans[N][500],q[500],no[500],pre[500];
 6 int main(){
 7     freopen("lottery.in","r",stdin);
 8     freopen("lottery.out","w",stdout);
 9     scanf("%d%d",&n,&l);
10     for(register int i=1;i<=n;i++) scanf("%d",&a[i]);
11     scanf("%d",&d);
12     pre[1]=1;
13     for(register int i=1;i<=d;i++) scanf("%d",&q[i]),no[q[i]]=1;
14     for(register int i=2;i<=l;i++) pre[i]=pre[i-1]+no[i-1]; 
15     for(register int len=1;len<=n-l;len++){
16         int dis=0,le=1,ri=le+len;
17         for(register int j=0;j<l;j++){
18             if(a[le+j]!=a[ri+j]) dis++;
19         }
20         ans[pre[dis]][le]++;
21         ans[pre[dis]][ri]++;
22         while(1){
23             if(ri+l>n) break;
24             dis-=(a[le]!=a[ri]);
25             dis+=(a[le+l]!=a[ri+l]);
26             le++,ri++;
27             ans[pre[dis]][le]++;
28             ans[pre[dis]][ri]++;
29         }
30     }
31     for(register int i=1;i<=n-l+1;i++){
32         for(register int j=1;j<=d;j++){
33             ans[j][i]+=ans[j-1][i];
34         }
35     }
36     for(register int i=1;i<=d;i++){
37         for(register int j=1;j<=n-l+1;j++){
38             printf("%d ",ans[pre[q[i]]][j]);
39         }
40         printf("\n");
41     }
42     return 0;
43 }

 以下是广告时间

——抓住了时间，却不会利用的人，终究也逃不过失败的命运。
【推广】 免费学中医，健康全家人
原文地址：https://www.cnblogs.com/Nelson992770019/p/11385740.html