Topcoder 13503 ConnectingGame

题目链接

Vjudge ConnectingGame Topcoder 13503 ConnectingGame

题目大意

有一个 (n imes m) 的字符矩阵，字符相同的地方组成一个区块，所有区块的都是四联通的，问是否存在方案，把每个区块染成红色或蓝色，使得不存在从上到下的一条蓝色的通路，同时不存在从左到右的一条红色的通路。

(1leq n,mleq 30)

思路

从找规律和看样例着手，观察这一组样例：

SSnukee
SKnuthe
SSSothe

画出来长这样：

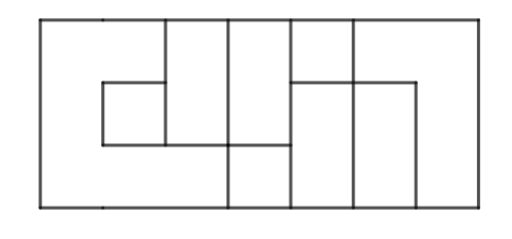
一组不存在通路的方案是这样的：

多画几组样例，能够发现把通路断开来的关键的地方都是如上图 “十字路口” 的地方，使得对角是相同颜色，相邻的是不同的颜色，把两条路同时断开了，于是猜结论：

图中存在 "十字路口" 是存在方案的必要条件

证明的话是一个简单的数学组合问题

（征求严谨证明中）

接下来考虑十字会如何产生一组解，我们沿着十字所划开来的边界走，直到走到矩阵的边缘，可以发现，一旦走到边缘，其实就相当于把整张图切成了四半，然后每一半内直接涂同一种颜色就是一组解了。

这个问题可以抽象到无向图上，有一张 ((n+1)(m+1)) 节点的无向图，有一个起点和若干终点，要求找到四条路径，分别从起点连到一个终点，并且路径两两不重合。

仔细想想会发现这是一个网络流问题，给所有终点建一个汇点连有向边过去，所有边的流量设为 (1)，然后检查最大流是否 (geq 4) 即可。不过呢，在这道题目中，并不是随便找四条分隔线就可以的，有如下几种特殊情况：

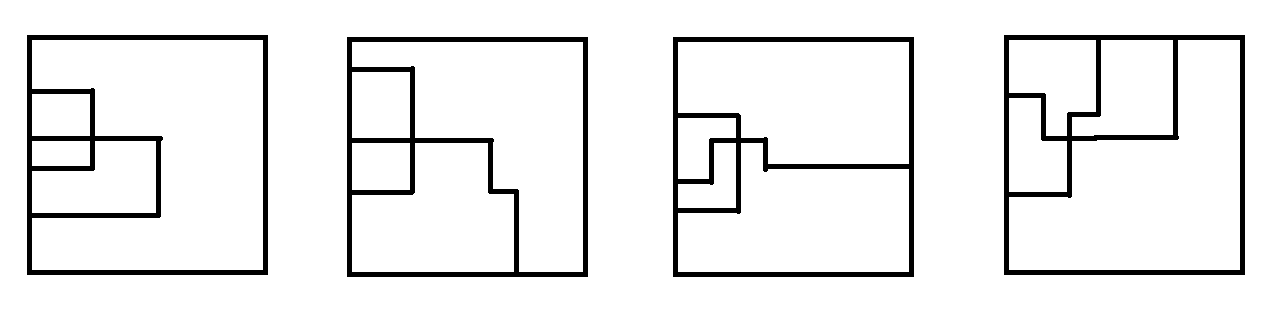
总结下来，线的分布要满足一些条件，

矩阵的一条边上的线数量 (leq 3)
任意两条边的线的数量 (leq 4)

任意两条边的线的数量 (leq 4) ，这就不是简单的求和关系了，似乎不好直接建图，但是每个边单独枚举流量这样效率十分低下。在这个地方我想了一段时间，找到了一个有趣的解决办法，

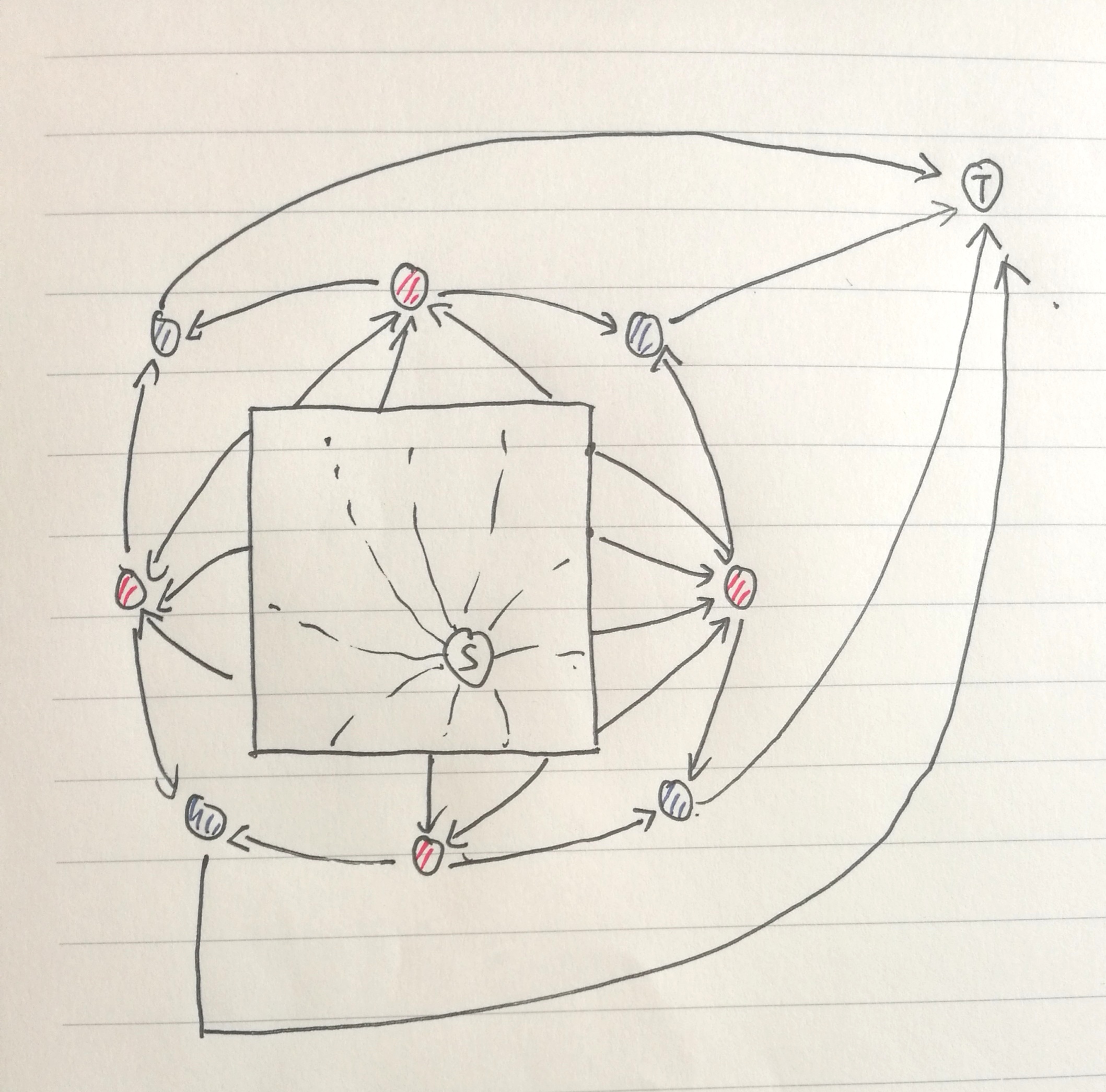
（无手写板人谢罪）如上图，先把每一条边界上的点连有向边指向对应的红点，相邻的两个红点再连边到对应的蓝点，蓝点再汇集到汇点处，这里所有边的容量全部为 (1)，画一下，可以发现刚好满足了上面的限制！

有了这样的解决方案，我们直接根据连通块分界线的关系建图，然后以 ”十字路口“ 为源点跑 (Dinic) 最大流即可，时间复杂度为 (O(n^6))，不过众所周知这个上界远远达不到，实际表现总耗时 (604ms)，非常快。

Code

#include<iostream>
#include<vector>
#include<cstring>
#include<queue>
#define mem(a,b) memset(a, b, sizeof(a))
#define rep(i,a,b) for(int i = (a); i <= (b); i++)
#define per(i,b,a) for(int i = (b); i >= (a); i--)
#define N 33
#define Inf 0x3f3f3f3f
using namespace std;

class ConnectingGame{
    public:
    int head[N*N], to[2*N*N], nxt[2*N*N];
    int origin[2*N*N], deg[N*N];
    int cap[2*N*N], dis[N*N], now[2*N*N];
    int cnt, T;
    queue<int> q;

    int n, m;
    vector<string> s;

    void init(){ mem(head, -1), cnt = -1; }
    void add_e(int a, int b, int id, int w){
        nxt[++cnt] = head[a], head[a] = cnt, to[cnt] = b;
        origin[cnt] = w, deg[a] += (w != 0);
        if(id == 2) add_e(b, a, 0, w);
        if(id == 1) add_e(b, a, 0, 0);
    }

    int f(int x, int y){ return x*(m+1)+y; }
    void build(){
        init();
        rep(i,0,n-1) rep(j,0,m-2){
            if(s[i][j] != s[i][j+1]) add_e(f(i,j+1), f(i+1,j+1), 2, 1); 
        }
        rep(i,0,n-2) rep(j,0,m-1){
            if(s[i][j] != s[i+1][j]) add_e(f(i+1,j), f(i+1,j+1), 2, 1);
        }
        int st = (n+1)*(m+1);
        rep(i,0,m) add_e(f(0,i), st+0, 1, 1), add_e(f(n,i), st+2, 1, 1);
        rep(i,0,n) add_e(f(i,0), st+1, 1, 1), add_e(f(i,m), st+3, 1, 1);
        rep(i,0,3) add_e(st+i, st+4+i, 1, 1), add_e(st+(i+1)%4, st+4+i, 1, 1);
        T = (n+1)*(m+1)+8;
        rep(i,0,3) add_e(st+4+i, T, 1, 1);
    }

    bool bfs(int S){
        mem(dis, 0), dis[S] = 1;
        q.push(S);
        while(!q.empty()){
            int cur = q.front(); q.pop();
            now[cur] = head[cur];
            for(int i = head[cur]; ~i; i = nxt[i]){
                if(cap[i] && !dis[to[i]])
                    dis[to[i]] = dis[cur]+1, q.push(to[i]);
            }
        }
        return dis[T];
    }

    int dfs(int x, int flow){
        if(x == T) return flow;
        int flown = 0;
        for(int i = now[x], y; ~i; i = nxt[i]){
            now[x] = i;
            if(cap[i] && dis[(y = to[i])] == dis[x]+1){
                int t = dfs(y, min(flow-flown, cap[i]));
                cap[i] -= t, cap[i^1] += t;
                flown += t;
                if(flown == flow) break;
            }
        }
        return flown;
    }

    string isValid(vector<string> board){
        s = board;
        n = s.size(), m = s[0].size();
        build();
        rep(i,0,(n+1)*(m+1)-1) if(deg[i] == 4){
            rep(e,0,cnt) cap[e] = origin[e];
            int flown = 0;
            while(bfs(i)) flown += dfs(i, Inf);
            if(flown >= 4) return "invalid";
        }
        return "valid";
    }
} solve;

int main(){
    int n;
    string s;
    vector<string> read;
    cin>>n;
    rep(i,1,n) cin>>s, read.push_back(s);
    cout<< solve.isValid(read) <<endl;
    return 0;
}

延伸：一种有趣的网络流建图方式

当时想出那个建图的方式只是一个偶然的灵感，事后自己感到疑惑，这个做法已经说明网络流具有解决有重合的流量限制问题的潜力，此问题是否仅仅是一个特殊解呢？

经过认真思考，我发现 任意边集流量限制的问题是具有通解的 ，只要通过适当的方式建图，就可以用最大流直接解决，逻辑并不复杂：

最开始我考虑了一个简单的问题：

有三个流，设流量分别为 (x,y,z)，有限制 (x+yleq a), (y+zleq b) ，同时三个流最终流量也有各自的限制，如何建图求出最大流（各自的流先前也有一系列的流量限制，即不一定能做到 (x=a,y=0,z=b) 的边界情况）。

先设计了 (4) 个辅助点的图，发现确实能解决两个约束，却同时把最终汇点的入流量给限制小了，把方程列出来，发现问题出在我们关注的流量有 (5) 个，即 (x,y,z,x+y,y+z)，想要这些变量不互相牵制，显然我们需要至少 (5) 个参数才行，于是经过调整，我顺利得到了该问题的图：

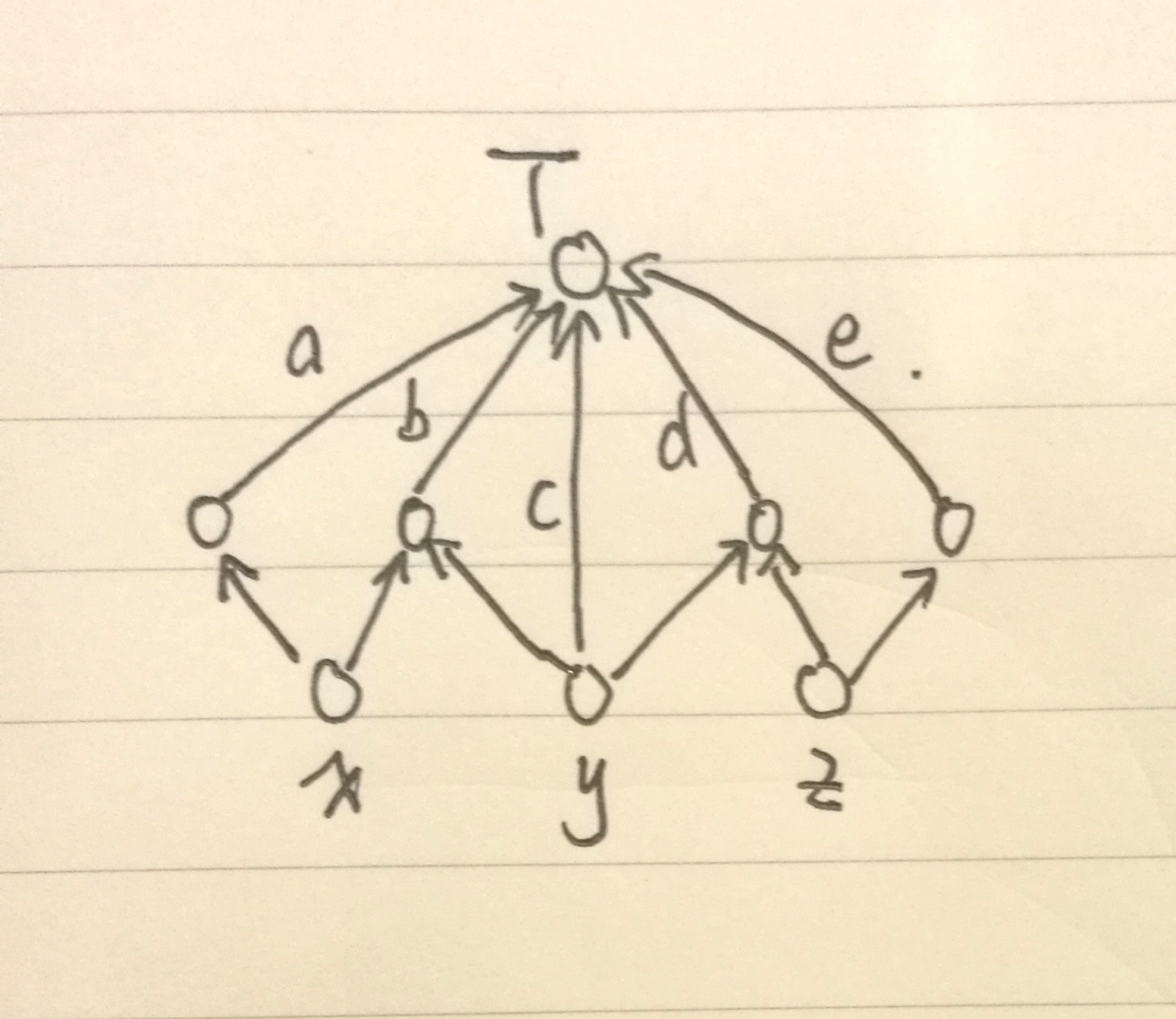
(a,b,c,d,e) 为所需的参数，是 (5) 条边的容量，剩下的边没有容量限制，设为 (Inf) 即可，得到方程组：

[egin{cases} xleq a+b\ yleq b+c+d\ zleq d+e\ x+yleq a+b+c+d\ y+zleq b+c+d+e end{cases} ]

将各自所需的限制带入其中，解出几个参数即可，为了方便，记 (overline{x}) 为流 (x) 的流量上限，解为：

[egin{cases} a=overline{x+y}-overline{y}\ b=overline{x}+overline{y}-overline{x+y}\ c=overline{x+y}+overline{y+z}-overline{x}-overline{y}-overline{z}\ d=overline{y}+overline{z}-overline{y+z}\ e=overline{y+z}-overline{y} end{cases} ]

看起来一切正常，不过这张图还对 (x+y+z) 作了隐性的限制，在这里

[x+y+zleq a+b+c+d+e=overline{x+y}+overline{y+z}-overline{y} ]

但是通过已有条件的简单不等式变换，应为

[x+y+zleq overline{x}+overline{z}+min(overline{x+y}-overline{x},overline{y+z}-overline{z}) ]

两者并不等价！例如 (overline{x}=1,overline{y}=3,overline{z}=4,overline{x+y}=3,overline{y+z}=6) 时，取 (x=1,y=1,z=4) 便是一组反例，这意味着我们之前建图时还是漏掉了一些关键信息，“没有限制” 也是一种性质，需要专门维护。

看来我们只能从完整的限制入手了，(x,y,z) 三个流共有 (7) 种限制，这里每一种都建一个点进行维护，画一画之后可以得到如下的图：

此时我们真正地把每一类限制都用参数对应起来了，它的解为：

[egin{cases} a=overline{y+z}+overline{x+z}-overline{x+y+z}-overline{z}\ b=overline{x+y}+overline{y+z}-overline{x+y+z}-overline{y}\ c=overline{x+y}+overline{x+z}-overline{x+y+z}-overline{x}\ d=overline{x+y+z}-overline{y+z}\ e=overline{x+y+z}-overline{x+z}\ f=overline{x+y+z}-overline{x+y}\ g=overline{x}+overline{y}+overline{z}-overline{x+y}-overline{y+z}-overline{z+x}+overline{x+y+z} end{cases} ]

对于我们没有限制的流量，可以通过解不等式，把其上界算出来，然后作为最大值带入解中，便可以很好地维护这样的关系了。

这样的思路可以拓展到 (k) 元流的情况，对于每一个大小 (>1) 的点集，建一个辅助点并向其连有向边，辅助点连向汇点的边容量即为方程参数的解，建成的图辅助点数 (2^k-k-1)，因为有

[sum_{i=0}^{2^d-1}popcount(i)=sum_{i=0}^dicdotinom{d}{i}=dcdotsum_{i=0}^dinom{d-1}{i-1}=dcdot2^{d-1} ]

从而边数为 ((k+2)cdot2^{k-1}-k-1)，网络流的时间复杂度为 (O(kcdot2^{2k-1}))，大约可以 (1s) 跑规模 (k=14) 的数据。

附 (k=4) 的图：

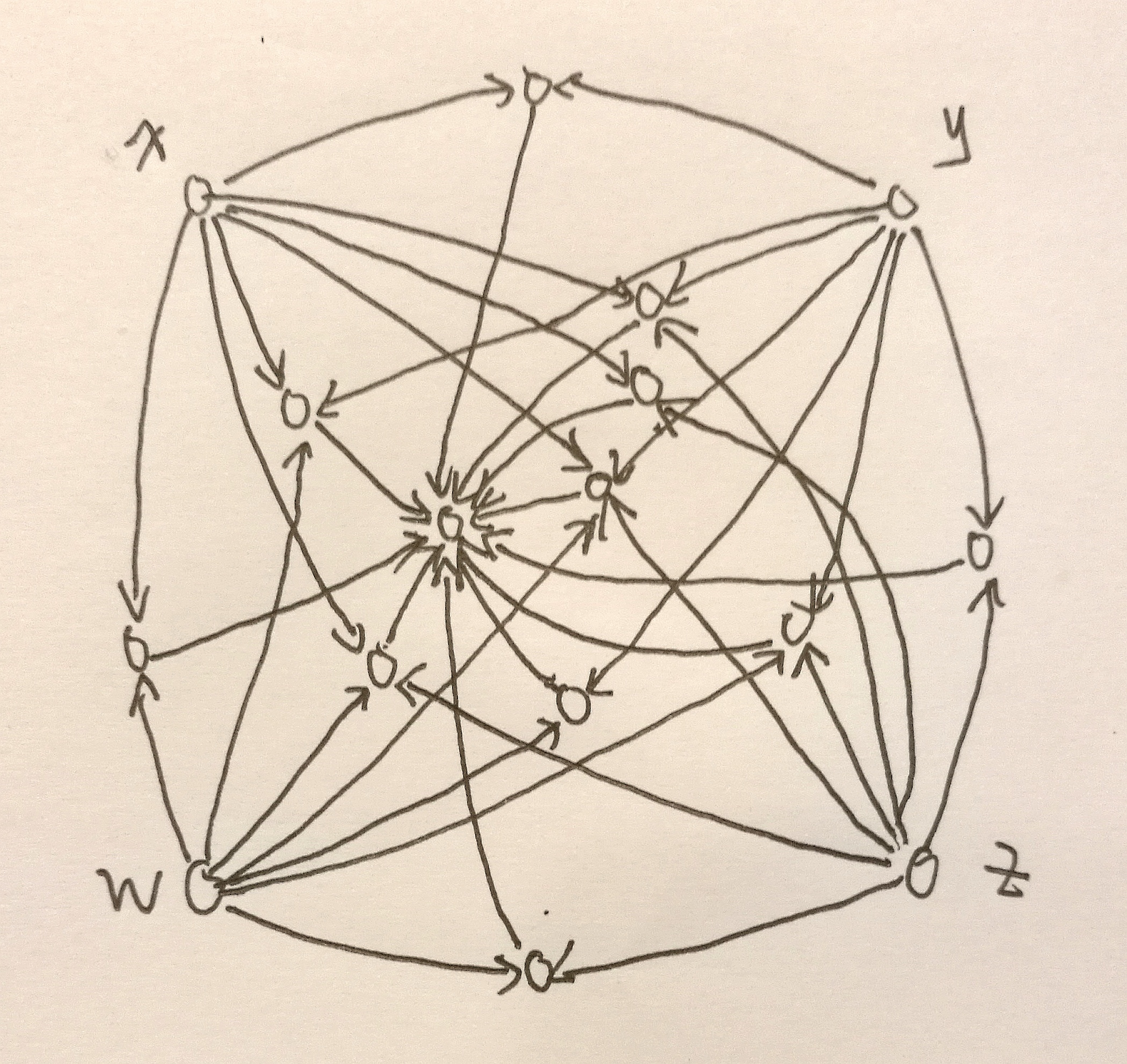
至此，我们用类似于线性规划的思路解决了一个有趣的问题，这个做法本人在百度和 (Google) 上都没有找到相似的信息，或许仅仅是在 (OI) 界比较冷门吧，~~但我们可以拿它来出毒瘤题了诶~~。