一、案例
There are N network nodes, labelled 1 to N.
Given times, a list of travel times as directededges times[i]=(u,v,w), where u is the source node, v is the target node, and w is the time it takes for a signal to travel from source to target.
Now, we send a signal from a certain node K. How long will it take for all nodes to receive the signal? If it is impossible, return -1.
有 N 个网络节点，标记为 1 到 N。
给定一个列表 times，表示信号经过有向边的传递时间。 times[i] = (u, v, w)，其中 u 是源节点，v 是目标节点， w 是一个信号从源节点传递到目标节点的时间。
现在，我们从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1。
Example 1:
输入：times = [[2,1,1],[2,3,1],[3,4,1]], N = 4, K = 2
输出：2
注意:
N 的范围在 [1, 100] 之间。
K 的范围在 [1, N] 之间。
times 的长度在 [1, 6000] 之间。
所有的边 times[i] = (u, v, w) 都有 1 <= u, v <= N 且 0 <= w <= 100。
二、Dijkstra
2.1 题目分析
这道题给了我们一些有向边，又给了一个结点K，问至少需要多少时间才能从K到达任何一个结点。这实际上是一个有向图求最短路径的问题，求出K点到每一个点到最短路径，然后取其中最大的一个就是需要的时间了。可以想成从结点K开始有水流向周围扩散，当水流到达最远的一个结点时，那么其他所有的结点一定已经流过水了。最短路径的常用解法有迪杰斯特拉算法 Dijkstra Algorithm, 弗洛伊德算法 Floyd-Warshall Algorithm, 和贝尔曼福特算法 Bellman-Ford Algorithm，其中，Floyd 算法是多源最短路径，即求任意点到任意点到最短路径，而 Dijkstra 算法和 Bellman-Ford 算法是单源最短路径，即单个点到任意点到最短路径。这里因为起点只有一个K，所以使用单源最短路径就行了。这三种算法还有一点不同，就是 Dijkstra 算法处理有向权重图时，权重必须为正，而另外两种可以处理负权重有向图，但是不能出现负环，所谓负环，就是权重均为负的环。为啥呢，这里要先引入松弛操作 Relaxtion，这是这三个算法的核心思想，当有对边 (u, v) 是结点u到结点v，如果 dist(v) > dist(u) + w(u, v)，那么 dist(v) 就可以被更新，这是所有这些的算法的核心操作。Dijkstra 算法是以起点为中心，向外层层扩展，直到扩展到终点为止。根据这特性，用 BFS 来实现时再好不过了，注意 while 循环里的第一层 for 循环，这保证了每一层的结点先被处理完，才会进入进入下一层，这种特性在用 BFS 遍历迷宫统计步数的时候很重要。对于每一个结点，都跟其周围的结点进行 Relaxtion（松弛） 操作，从而更新周围结点的距离值。为了防止重复比较，需要使用 visited 数组来记录已访问过的结点，最后在所有的最小路径中选最大的返回，注意，如果结果 res 为 INT_MAX，说明有些结点是无法到达的，返回 -1。普通的实现方法的时间复杂度为 O(V^2 + E)，基于优先队列的实现方法的时间复杂度为 O(E + VlogV)，其中V和E分别为结点和边的个数，这里多说一句，Dijkstra 算法这种类贪心算法的机制，使得其无法处理有负权重的最短距离，还好这道题的权重都是正数，参见代码如下。
2.2 解法一
如果对于所有的边权值均为1，那么Dijkstra算法可以用BFS实现，也就是普通的dijkstra。
1 class Solution {
2 public:
3 int networkDelayTime(vector<vector<int>>& times, int N, int K) {
4 vector<vector<int> > edges(N + 1, vector<int>(N + 1, -1));
5 for(auto item : times){
6 edges[item[0]][item[1]] = item[2];
7 }
8 queue<int> q{{K}};
9 vector<int> dis(N+1, INT_MAX);
10 dis[K] = 0;
11 vector<bool> visited(N+1, false);
12 visited[K] = true;
13 while(!q.empty()){
14 int u = q.front();
15 q.pop();
16 visited[u] = false;
17 for(int v=1; v<=N; v++){
18 if(edges[u][v] != -1 && dis[u] + edges[u][v] < dis[v]){
19 dis[v] = dis[u] + edges[u][v];
20 if(visited[v])
21 continue;
22 visited[v] = true;
23 q.push(v);
24 }
25 }
26 }
27 int ans = 0;
28 for(int i=1; i<=N; i++)
29 ans = max(ans, dis[i]);
30 return ans == INT_MAX ? -1 : ans;
31 }
32 };
2.2 解法二
优先队列优化的dijkstra，基于优先队列的实现方法的分为集中情况，当地曾实现是二叉堆时，时间复杂度为O((E+V)logV)，当底层实现使用二项堆时，时间复杂度是O((E+V)logV)，当底层数据结构使用斐波那契堆，时间复杂度为时间复杂度为 O(E + VlogV)，其中V和E分别为结点和边的个数，这里多说一句，Dijkstra 算法这种类贪心算法的机制，使得其无法处理有负权重的最短距离，还好这道题的权重都是正数，代码如下：
1 int networkDelayTime(vector<vector<int>>& times, int N, int K)
2 {
3 //基于优先队列的dijkstra
4
5 //自定义数据结构，并重载>操作符，实现小顶堆
6 struct Node
7 {
8 int index;
9 int distance;
10 Node(int x = 0, int y = 0)
11 {
12 index = x;
13 distance = y;
14 }
15
16 //less：大顶堆
17 bool operator<(const Node item) const
18 {
19 return distance < item.distance;
20 }
21
22 //小顶堆
23 bool operator>(const Node item) const
24 {
25 return distance > item.distance;
26 }
27 };
28
29 //邻接矩阵
30 unordered_map<int, vector<Node> > graph;
31 for (auto & item : times)
32 {
33 graph[item[0]].push_back(Node(item[1], item[2]));
34 }
35
36 //小顶堆的优先队列
37 priority_queue<Node, vector<Node>, greater<Node>> q;
38
39 //源节点入队
40 q.push(Node(K, 0));
41
42 //结果集
43 vector<int> dist(N + 1, INT_MAX);
44 dist[K] = 0;
45
46 //访问标记数组
47 unordered_set<int> visited;
48
49 //开始广度优先搜索
50 while (!q.empty())
51 {
52 Node node = q.top();
53 q.pop();
54 int u = node.index, curmindist = node.distance;
55
56 //已经访问的节点不再访问
57 if (visited.count(u))
58 continue;
59 visited.insert(u);
60 for (auto item : graph[u])
61 {
62 int v = item.index, costuv = item.distance;
63 //如果满足条件，就进行松弛，并入队
64 if (curmindist + costuv < dist[v])
65 {
66 dist[v] = curmindist + costuv;
67 q.push(Node(v, dist[v]));
68 }
69 }
70 }
71
72 //统计结果，如果存在无法达到的节点，就返回-1；
73 int ans = 0;
74 for (int i = 1; i <= N; i++)
75 {
76 if (dist[i] == INT_MAX)
77 return -1;
78 ans = max(ans, dist[i]);
79 }
80
81 return ans;
82 }
三、Bellman Ford
下面来看基于 Bellman-Ford 算法的解法，时间复杂度是 O(VE)，V和E分别是结点和边的个数。这种算法是基于 DP 来求全局最优解，原理是对图进行 V - 1 次松弛操作，这里的V是所有结点的个数（为啥是 V-1 次呢，因为最短路径最多只有 V-1 条边，所以只需循环 V-1 次），在重复计算中，使得每个结点的距离被不停的更新，直到获得最小的距离，这种设计方法融合了暴力搜索之美，写法简洁又不失优雅。之前提到了，Bellman-Ford 算法可以处理负权重的情况，但是不能有负环存在，一般形式的写法中最后一部分是检测负环的，如果存在负环则报错。不能有负环原因是，每转一圈，权重和都在减小，可以无限转，那么最后的最小距离都是负无穷，无意义了。没有负环的话，V-1 次循环后各点的最小距离应该已经收敛了，所以在检测负环时，就再循环一次，如果最小距离还能更新的话，就说明存在负环。这道题由于不存在负权重，所以就不检测了，参见代码如下：
解法三：Bellman Ford
1 int networkDelayTime(vector<vector<int>>& times, int N, int K)
2 {
3 int inf = 0x3f3f3f3f3f;
4 vector<int> dist(N + 1, inf);
5 dist[K] = 0;
6 for (int i = 1; i < N; i++) //外循环循环N-1次，n为顶点个数
7 {
8 for (auto & item : times) //内循环循环m次，m为边的个数，即枚举每一条边
9 {
10 int u = item[0], v = item[1], w = item[2];
11 if (dist[v] > dist[u] + w) //尝试对每一条边进行松弛，与Dijkstra算法相同
12 dist[v] = dist[u] + w;
13 }
14 }
15
16
17 //检测负权回路
18 int hasCycle = 0;
19 for (int i = 0; i < times.size(); i++)
20 {
21 int u = times[i][0], v = times[i][1], w = times[i][2];
22 if (dist[v] > dist[u] + w)
23 {
24 hasCycle = 1;
25 break;
26 }
27 }
28
29 if (hasCycle)
30 {
31 cout << "改图有负权回路" << endl;
32 return -1;
33 }
34 else
35 {
36 int ans = 0;
37 for (int i = 1; i < N; i++)
38 {
39 if (dist[i] == inf)
40 return -1;
41 ans = max(ans, dist[i]);
42 }
43 return ans;
44 }
45 }
四、SPFA
下面这种解法是 Bellman Ford 解法的优化版本。之所以能提高运行速度，是因为使用了队列 queue，这样对于每个结点，不用都松弛所有的边，因为大多数的松弛计算都是无用功。优化的方法是，若某个点的 dist 值不变，不去更新它，只有当某个点的 dist 值被更新了，才将其加入 queue，并去更新跟其相连的点，同时还需要加入 HashSet，以免被反复错误更新，这样的时间复杂度可以优化到 O(E+V)。Java 版的代码在评论区三楼，旅叶声称可以 beat 百分之九十多，但博主改写的这个 C++ 版本的却只能 beat 百分之二十多。参见代码如下：
解法四：SPFA
1 int networkDelayTime1(vector<vector<int>>& times, int N, int K)
2 {
3 //定义一个结构题，将节点和代价统一
4 struct Node {
5 int index;
6 int distance;
7 Node(int x = 0, int y = 0)
8 {
9 index = x;
10 distance = y;
11 }
12 };
13
14 //建立邻接矩阵
15 unordered_map<int, vector<Node> > graph;
16 for (auto & item : times)
17 graph[item[0]].push_back(Node(item[1], item[2]));
18
19 //结果集
20 int inf = 0x3f3f3f3f3f;
21 vector<int> dist(N + 1, inf);
22 dist[K] = 0;
23
24 //用队列存储更新过的节点
25 queue<int> q;
26 q.push(K);
27
28 //防止二次入队
29 vector<bool> visited(N + 1, false);
30 visited[K] = true;
31
32 while (!q.empty())
33 {
34 int u = q.front();
35 q.pop();
36 visited[u] = false;
37 for (auto & item : graph[u])
38 {
39 int v = item.index, costuv = item.distance;
40 if (dist[v] > dist[u] + costuv)
41 {
42 dist[v] = dist[u] + costuv;
43 if (visited[v])
44 continue;
45 visited[v] = true;
46 q.push(v);
47 }
48 }
49 }
50
51 int ans = 0;
52 for (int i = 1; i <= N; i++)
53 {
54 if (dist[i] == inf)
55 return -1;
56 ans = max(ans, dist[i]);
57 }
58
59 return ans;
60 }
四、Floyd
4.1 题目分析
最后再来说说这个 Floyd 算法，这也是一种经典的动态规划算法，目的是要找结点i到结点j的最短路径。而结点i到结点j的走法就两种可能，一种是直接从结点i到结点j，另一种是经过若干个结点k到达结点j。所以对于每个中间结点k，检查 dist(i, k) + dist(k, j) < dist(i, j) 是否成立，成立的话就松弛它，这样遍历完所有的结点k，dist(i, j) 中就是结点i到结点j的最短距离了。时间复杂度是 O(V^3)，处处透露着暴力美学。除了这三种算法外，还有一些很类似的优化算法，比如 Bellman-Ford 的优化算法- SPFA 算法，还有融合了 Bellman-Ford 和 Dijkstra 算法的高效的多源最短路径算法- Johnson 算法，这里就不过多赘述了，感兴趣的童鞋可尽情的 Google 之～
解法五：Floyd
1 int networkDelayTime1(vector<vector<int>>& times, int N, int K)
2 {
3 //建立结果集
4 int inf = 0x3f3f3f3f;
5 vector<vector<int> > dist(N + 1, vector<int>(n + 1, inf));
6
7 //对结果集进行初始化
8 for (int i = 1; i <= N; i++)
9 dist[i][i] = 0;
10
11 for (auto & item : times)
12 {
13 dist[item[0]][item[1]] = item[2];
14 }
15
16 //进行松弛
17 for (int k = 1; k <= N; k++)
18 {
19 for (int i = 1; i <= N; i++)
20 {
21 for (int j = 1; j <= N; j++)
22 {
23 if (dist[i][j] > dist[i][k] + dist[k][j])
24 dist[i][j] = dist[i][k] + dist[k][j];
25 }
26 }
27 }
28
29 //对结果进行分析
30 int ans = 0;
31 for (int i = 1; i <= N; i++)
32 {
33 if (dist[K][i] == inf)
34 return -1;
35 ans = max(dist[K][i], ans);
36 }
37 return ans;
38 }
4.2 Floyd算法理论分析
Floyd-傻子也能看懂的弗洛伊德算法
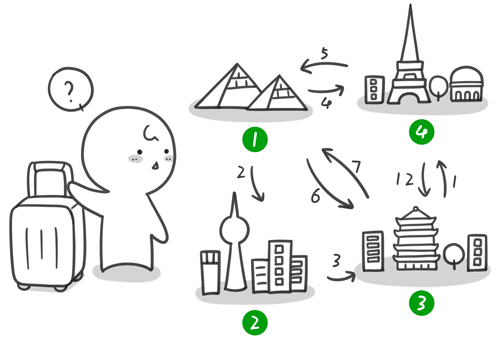
暑假，小哼准备去一些城市旅游。有些城市之间有公路，有些城市之间则没有，如下图。为了节省经费以及方便计划旅程，小哼希望在出发之前知道任意两个城市之前的最短路程。
上图中有4个城市8条公路，公路上的数字表示这条公路的长短。请注意这些公路是单向的。我们现在需要求任意两个城市之间的最短路程，也就是求任意两个点之间的最短路径。这个问题这也被称为“多源最短路径”问题。
现在回到问题：如何求任意两点之间最短路径呢？通过之前的学习我们知道通过深度或广度优先搜索可以求出两点之间的最短路径。所以进行n2遍深度或广度优先搜索，即对每两个点都进行一次深度或广度优先搜索，便可以求得任意两点之间的最短路径。可是还有没有别的方法呢
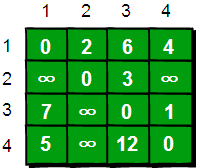
假如现在只允许经过1号顶点，求任意两点之间的最短路程，应该如何求呢？只需判断e[i][1]+e[1][j]是否比e[i][j]要小即可。e[i][j]表示的是从i号顶点到j号顶点之间的路程。e[i][1]+e[1][j]表示的是从i号顶点先到1号顶点，再从1号顶点到j号顶点的路程之和。其中i是1~n循环，j也是1~n循环，代码实现如下。
1 for (i = 1; i <= n; i++)
2 {
3 for (j = 1; j <= n; j++)
4 {
5 if (e[i][j] > e[i][1] + e[1][j])
6 e[i][j] = e[i][1] + e[1][j];
7 }
8 }
在只允许经过1号顶点的情况下，任意两点之间的最短路程更新为：
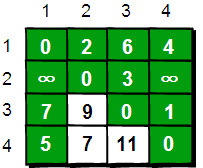
通过上图我们发现：在只通过1号顶点中转的情况下，3号顶点到2号顶点（e[3][2]）、4号顶点到2号顶点（e[4][2]）以及4号顶点到3号顶点（e[4][3]）的路程都变短了。
接下来继续求在只允许经过1和2号两个顶点的情况下任意两点之间的最短路程。如何做呢？我们需要在只允许经过1号顶点时任意两点的最短路程的结果下，再判断如果经过2号顶点是否可以使得i号顶点到j号顶点之间的路程变得更短。即判断e[i][2]+e[2][j]是否比e[i][j]要小，代码实现为如下。
1 //经过1号顶点
2 for(i=1;i<=n;i++)
3 for(j=1;j<=n;j++)
4 if (e[i][j] > e[i][1]+e[1][j])
5 e[i][j]=e[i][1]+e[1][j];
6 //经过2号顶点
7 for(i=1;i<=n;i++)
8 for(j=1;j<=n;j++)
9 if (e[i][j] > e[i][2]+e[2][j])
10 e[i][j]=e[i][2]+e[2][j];
在只允许经过1和2号顶点的情况下，任意两点之间的最短路程更新为：
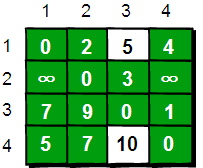通过上图得知，在相比只允许通过1号顶点进行中转的情况下，这里允许通过1和2号顶点进行中转，使得e[1][3]和e[4][3]的路程变得更短了。
同理，继续在只允许经过1、2和3号顶点进行中转的情况下，求任意两点之间的最短路程。任意两点之间的最短路程更新为：
最后允许通过所有顶点作为中转，任意两点之间最终的最短路程为：
整个算法过程虽然说起来很麻烦，但是代码实现却非常简单，核心代码只有五行：
1 for(k=1;k<=n;k++)
2 for(i=1;i<=n;i++)
3 for(j=1;j<=n;j++)
4 if(e[i][j]>e[i][k]+e[k][j])
5 e[i][j]=e[i][k]+e[k][j];
这段代码的基本思想就是：最开始只允许经过1号顶点进行中转，接下来只允许经过1和2号顶点进行中转……允许经过1~n号所有顶点进行中转，求任意两点之间的最短路程。用一句话概括就是：从i号顶点到j号顶点只经过前k号点的最短路程。
1 #include <iostream>
2 #include <stdio.h>
3
4 int main()
5 {
6 int e[10][10], k, i, j, n, m, t1, t2, t3;
7 int inf = 99999999; //用inf(infinity的缩写)存储一个我们认为的正无穷值
8 //读入n和m，n表示顶点个数，m表示边的条数
9 scanf("%d %d", &n, &m);
10 //初始化
11 for (i = 1; i <= n; i++)
12 for (j = 1; j <= n; j++)
13 if (i == j)
14 e[i][j] = 0;
15 else
16 e[i][j] = inf;
17 //读入边
18 for (i = 1; i <= m; i++)
19 {
20 scanf("%d %d %d", &t1, &t2, &t3);
21 e[t1][t2] = t3;
22 }
23 //Floyd-Warshall算法核心语句
24 for (k = 1; k <= n; k++)
25 for (i = 1; i <= n; i++)
26 for (j = 1; j <= n; j++)
27 if (e[i][j] > e[i][k] + e[k][j])
28 e[i][j] = e[i][k] + e[k][j];
29 //输出最终的结果
30 for (i = 1; i <= n; i++)
31 {
32 for (j = 1; j <= n; j++)
33 {
34 printf("%10d", e[i][j]);
35 }
36 printf("
");
37 }
38 return 0;
39 }
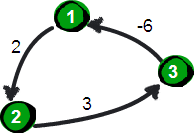
另外需要注意的是：Floyd-Warshall算法不能解决带有“负权回路”（或者叫“负权环”）的图，因为带有“负权回路”的图没有最短路。例如下面这个图就不存在1号顶点到3号顶点的最短路径。因为1->2->3->1->2->3->…->1->2->3这样路径中，每绕一次1->-2>3这样的环，最短路就会减少1，永远找不到最短路。其实如果一个图中带有“负权回路”那么这个图则没有最短路。
五、总结
最短路算法
最短路算法的分类：
单源最短路
所有边权都是正数
朴素的Dijkstra算法 O(n^2) 适合稠密图
堆优化版的Dijkstra算法 O(mlog n)（m是图中节点的个数）适合稀疏图
存在负权边
Bellman-Ford O(nm)
spfa 一般O(m),最坏O(nm)
多源汇最短路
Floyd算法 O(n^3)