在线性规划中的单纯形法与内点法(原理、步骤以及matlab实现)(一)中,我们讨论了单纯形法的原理和普通单纯形法的应用,本文接着讨论大M法、两阶段法和对偶单纯形法
2.2 Big M Method (大M法)
通常,我们遇到的问题约束条件不是像普通单纯形法中的形式,就是说有可能会符号为大于等于形式的不等式,这时,初始可行基的选择就不是那么容易了。这种情况下,我们可以利用大M法。下面举例说明应用

solution
通过引入slack或者surplus将不等式约束转为等式约束,并且将最小化问题转为最大化问题
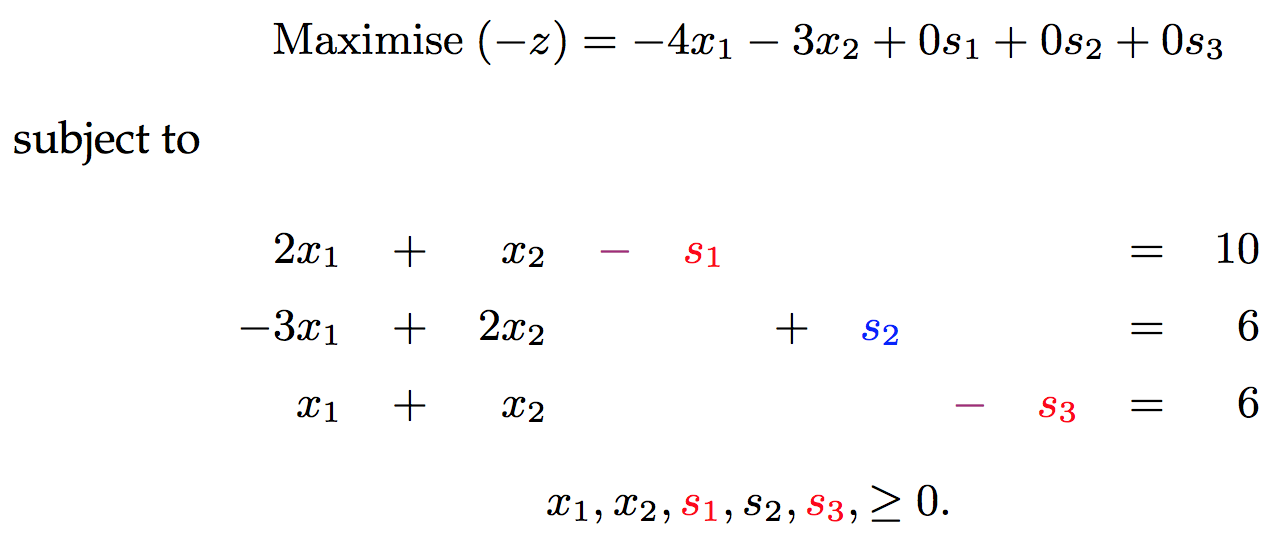
在这个形式中,初始可行基不是很容易选出,因为s1和s3的系数都是-1。这时我们可以引入额外的两个人工变量A1和A2,原问题转为:
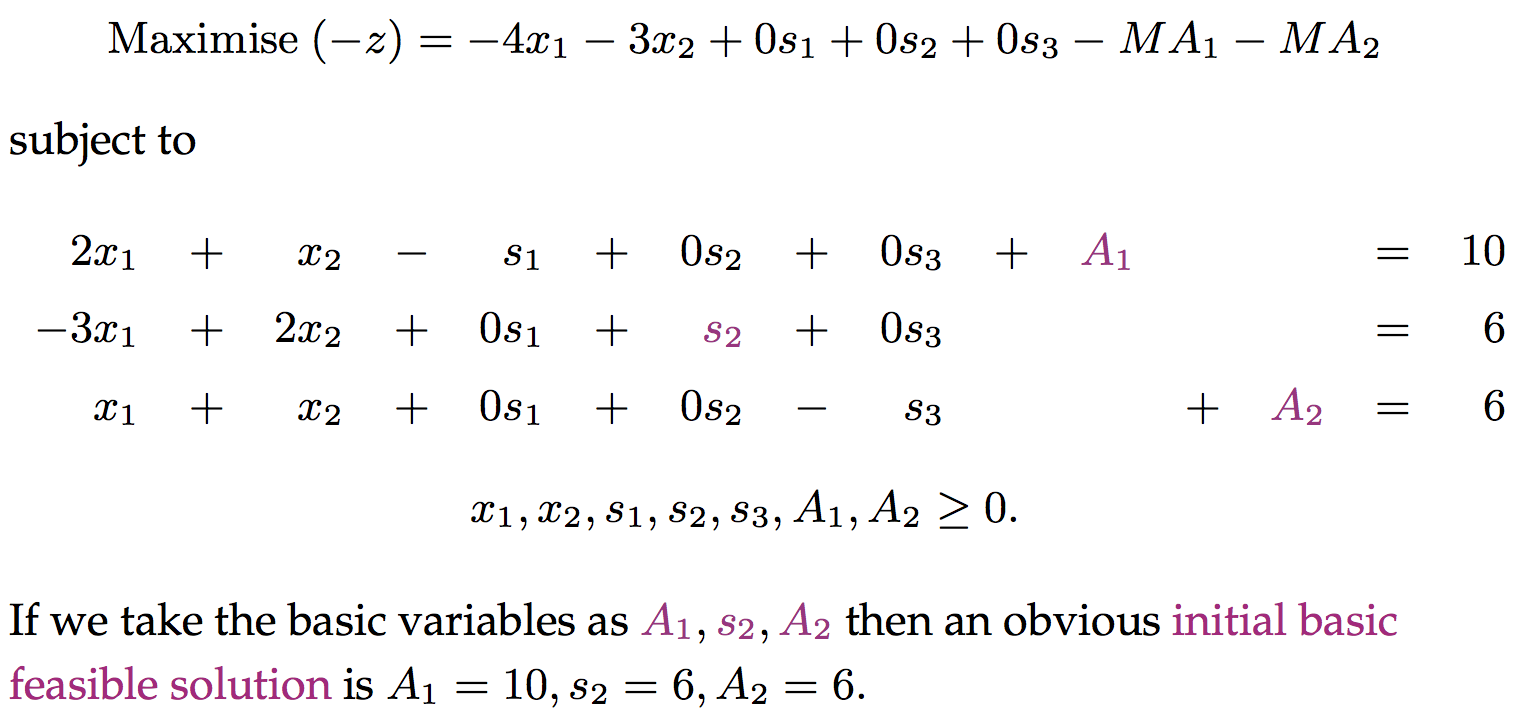
在目标函数中还引入了新的系数M,M是一个极大的数,因此要使得目标函数的值最大,A1和A2必须为0
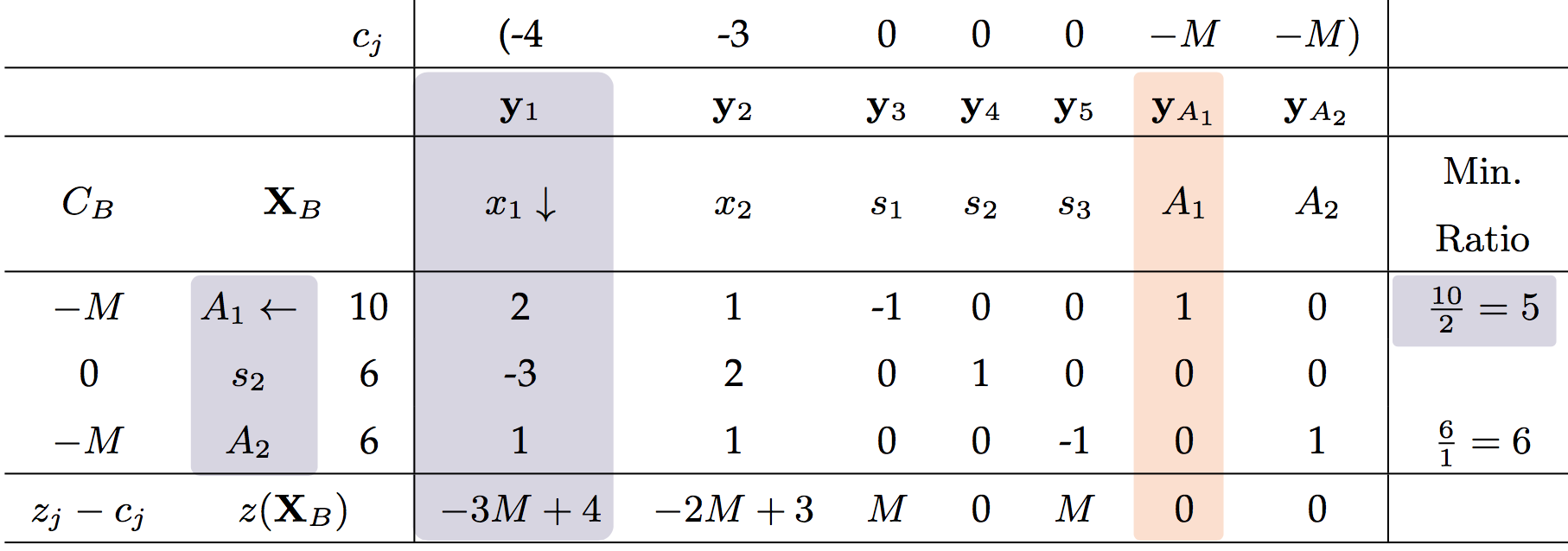
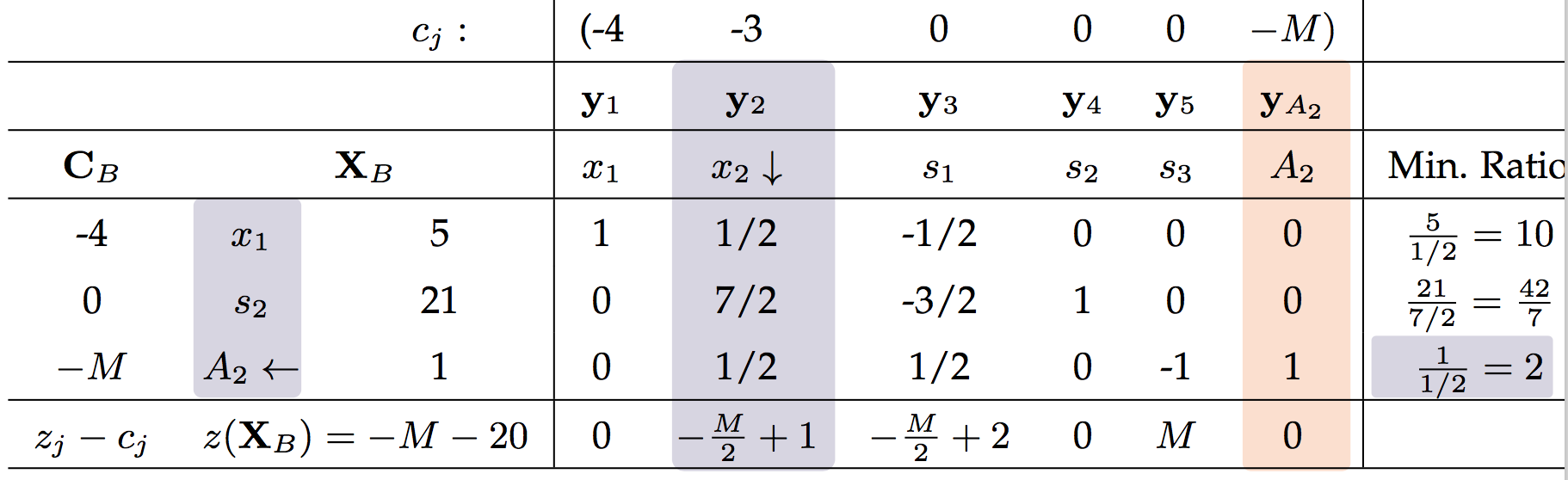
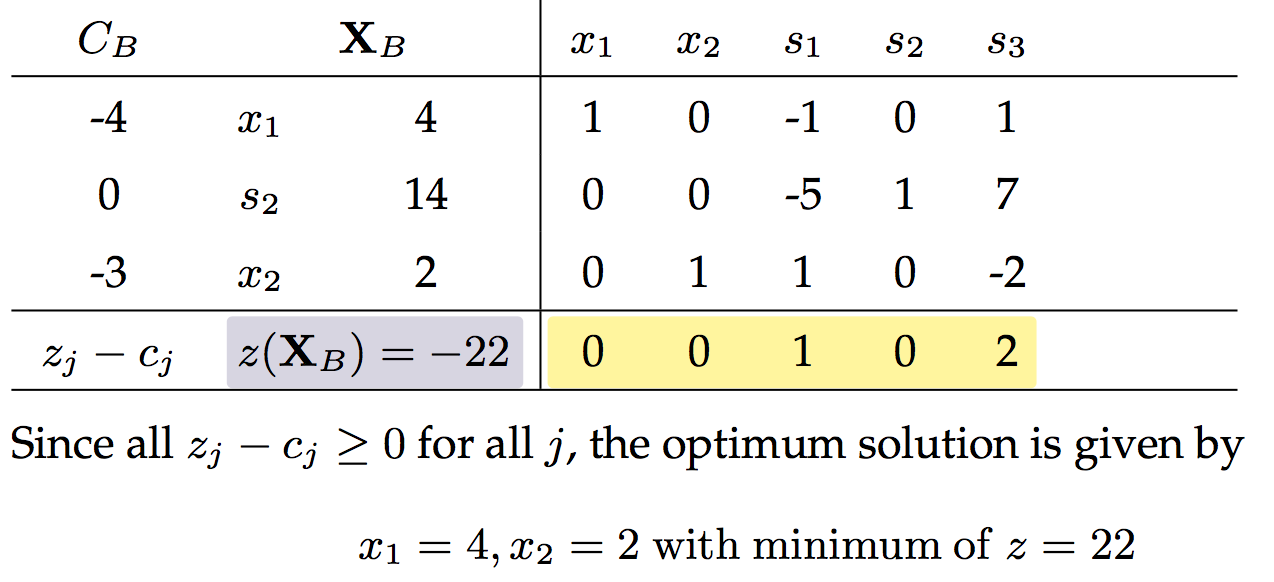
matlab实现
linprog():
记住:该函数的问题形式必须是最小化形式,并且右端值符号没有限制,但是不等号必须是小于等于
f = [4 3]; A = [-2 -1; -3 2; -1 -1]; b = [-10 6 -6]; [x, fval] = linprog(f, A, b)

revised():
c = [4 3]; A = [2 1; -3 2; 1 1]; b = [10 6 6]; inq = [1 -1 1]; revised(c, b, A, inq, 1)
运行结果:

2.3 Two-phase Method(两阶段法)
先来看一下大M法和两阶段法的联系和区别:

两阶段法中第一阶段构造了一个只有人工变量的新的目标函数,使得引入的人工变量为零。第二阶段使用第一阶段迭代的tableau继续迭代。可以看到其实大M法和两阶段法本质没有区别,只是将两步糅合成为一步。下面举例说明两阶段法的应用:

这道题可以用大M法解决,不过这里使用两阶段法
第一阶段,引入新的人工变量,并且构造新的目标函数(使人工变量为零)

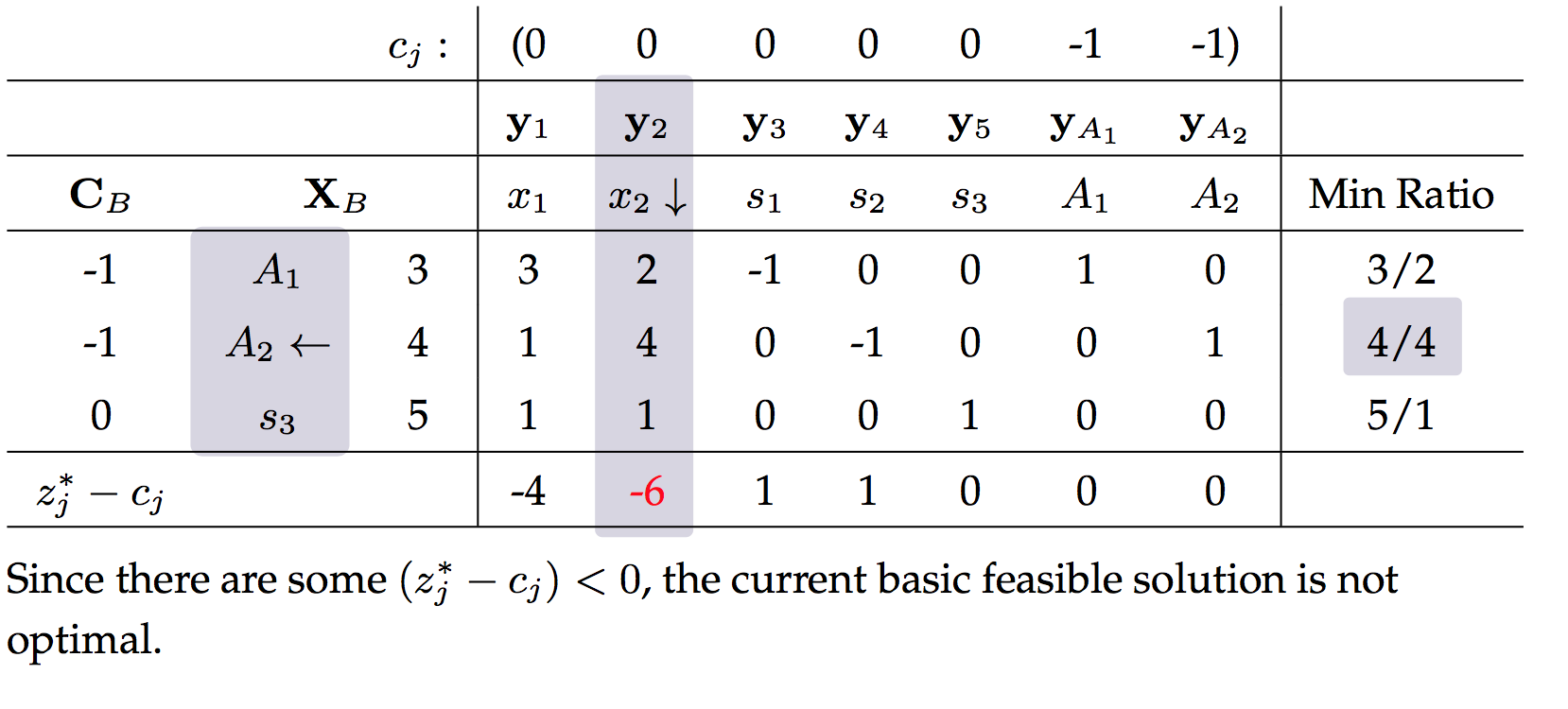
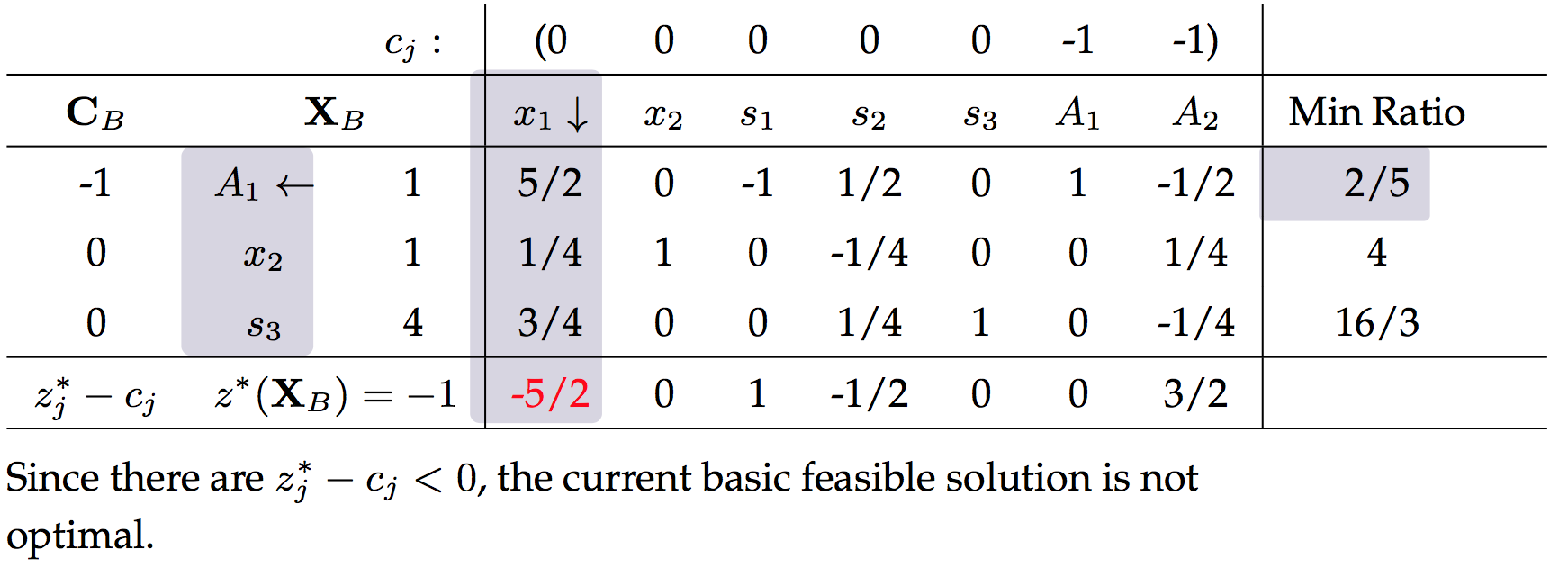
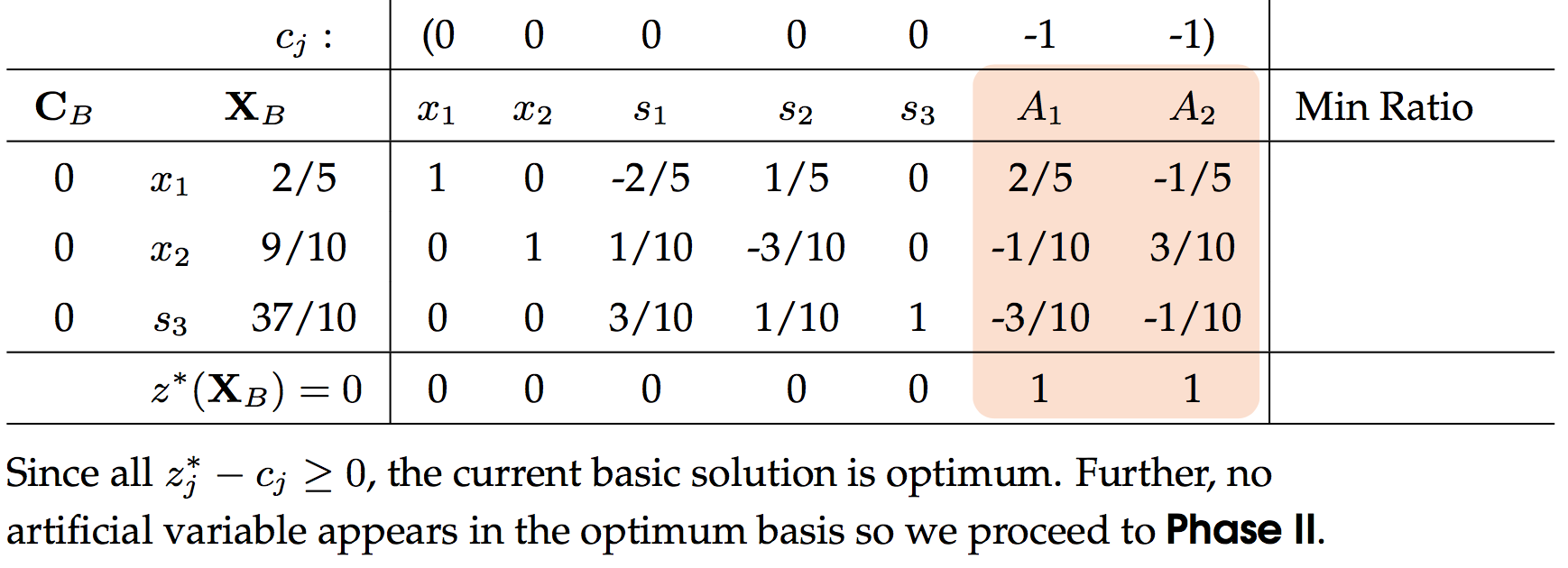
到这里,人工变量已经成为非基变量,即取零使得构造的目标函数值最优
进入第二阶段

这阶段的主要工作是:
1.使用原来的目标函数
2.初始开始迭代的基可行解是沿用上一阶段最后的迭代结果

下面开始迭代:
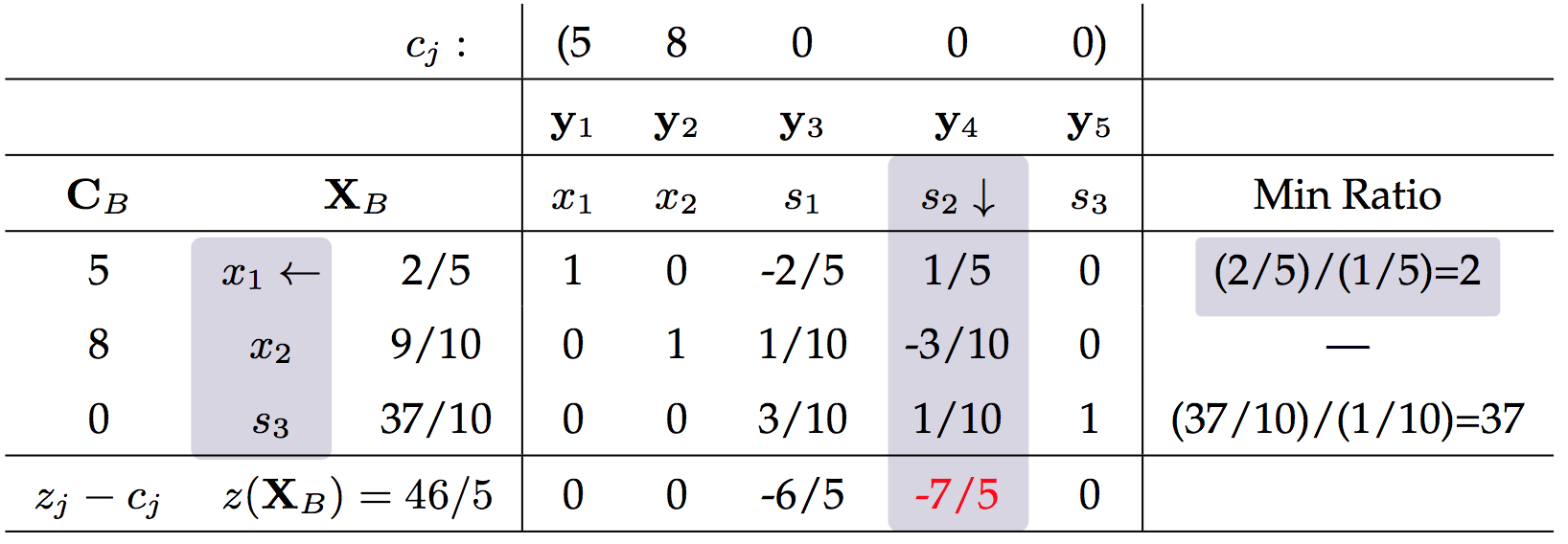
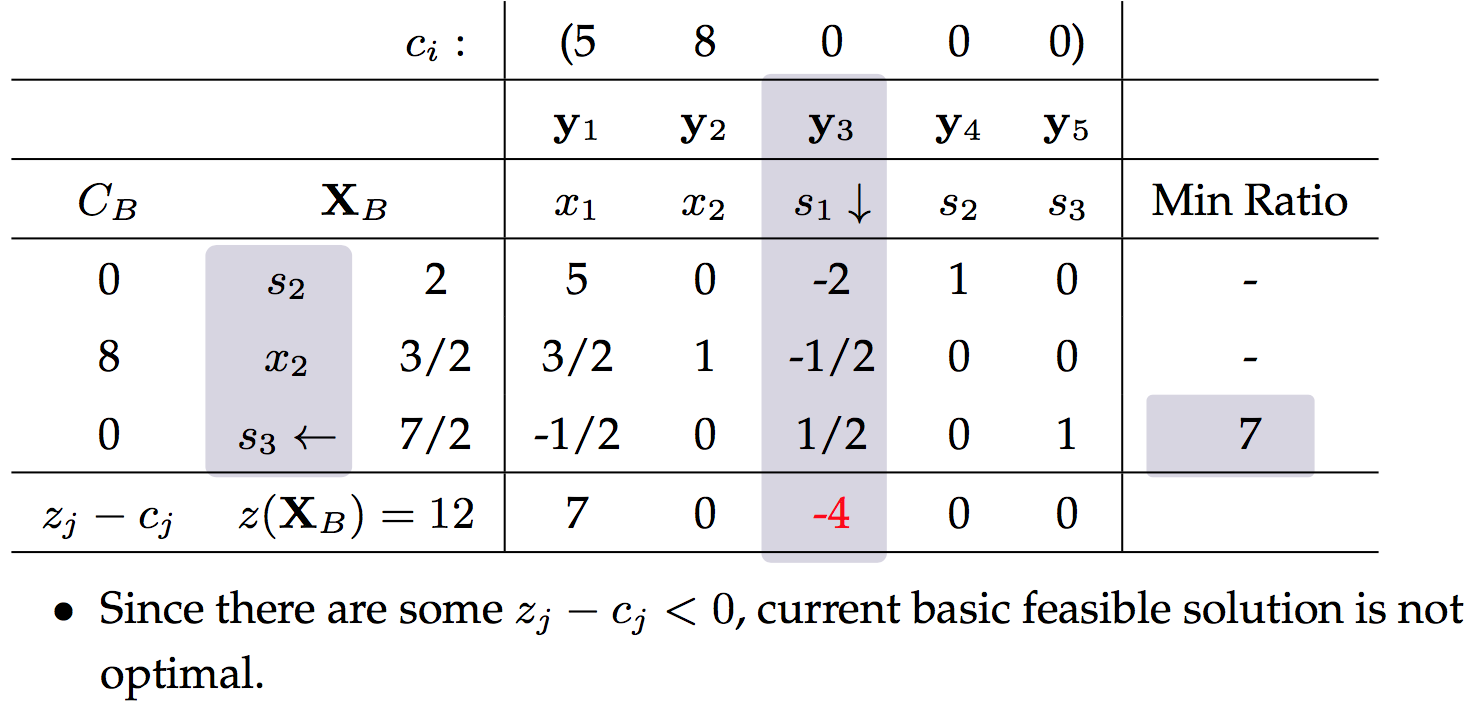
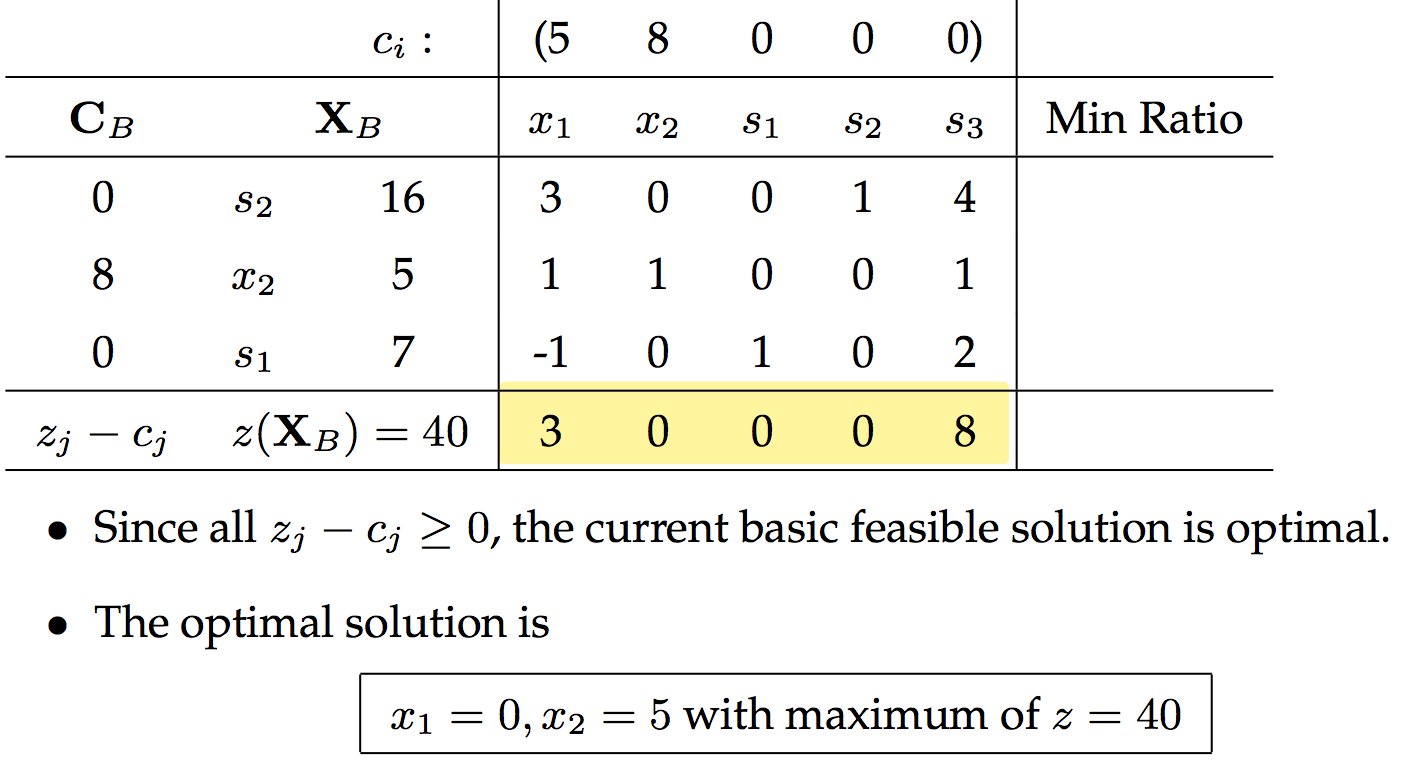
感兴趣的朋友可以用大M法解答
matlab实现:
linprog():
f = [-5 -8]; A = [-3 -2; -1 -4; 1 1]; b = [-3 -4 5]; lb = [0 0]; [x, fval] = linprog(f, A, b, [], [], lb)
运行结果:
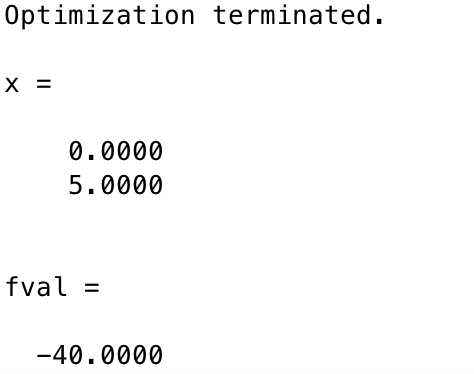
revised():
c = [5 8]; A = [3 2; 1 4; 1 1]; b = [3 4 5]; inq = [1 11 -1]; revised(c, b, A, inq, 0)
运行结果:
