所谓花,就是如下图所示的一个奇环:
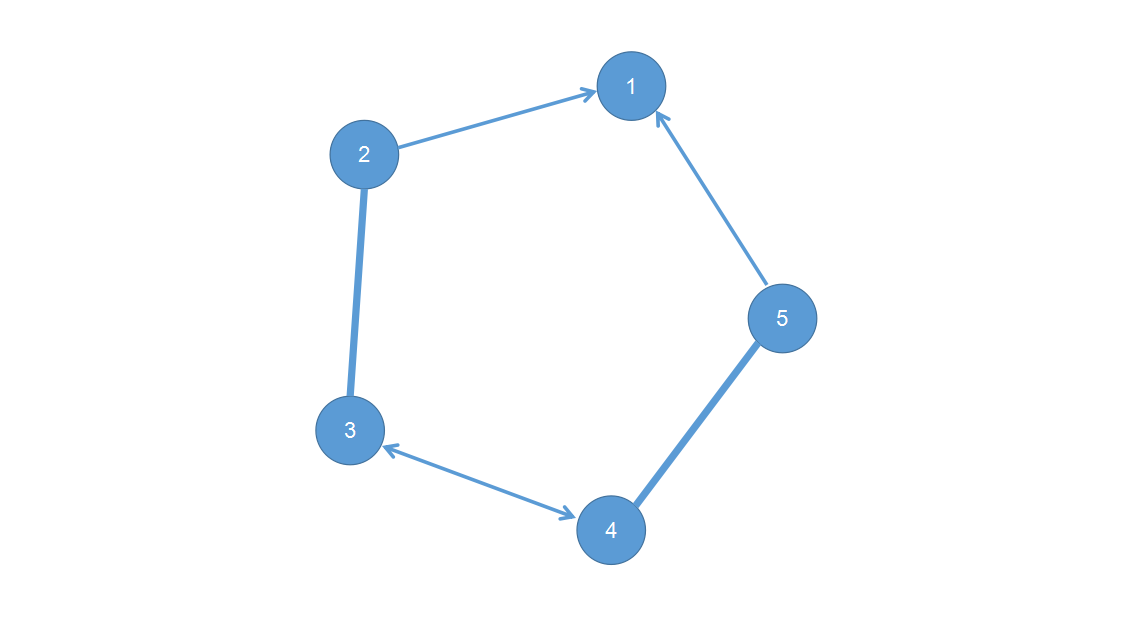
本文中粗边代表现在的匹配边,细边代表该点的前驱(后文会讲解前驱是什么,现在只需要知道每个点和它的前驱在原图中一定是有边的)。
如图所示,一朵包含(2k+1)个点的花一定至多包含(k)条匹配边,于是总会剩下一个未匹配的点,上图中即为(1)号点。
那么我们可以发现,如果有另外一个点想要与花中的某个点(v)匹配,那么有两种情况:1、(v)是未匹配的点(即1号点),那么直接与(v)匹配即可。2、(v)是已经匹配的点,这时只要将花中的匹配状况修改,使得(v)变成未匹配的那个点即可。
综上所述,只要花中的点没有向外匹配,我们总是可以使得外部的一个点和花中任意一个点匹配,因此花的性质和点其实很相似。我们将花缩成一个点来处理,就可以解决出现奇环的问题。以上思想就是带花树算法的核心。
总之分割一下好了
带花树算法的过程其实和(bfs)版本的匈牙利是很相似的,都是找出一个交错树,交错树可能长这样(注意每个蓝色点可能有多个橙色儿子,但是每个橙色点只能有一个蓝色儿子):
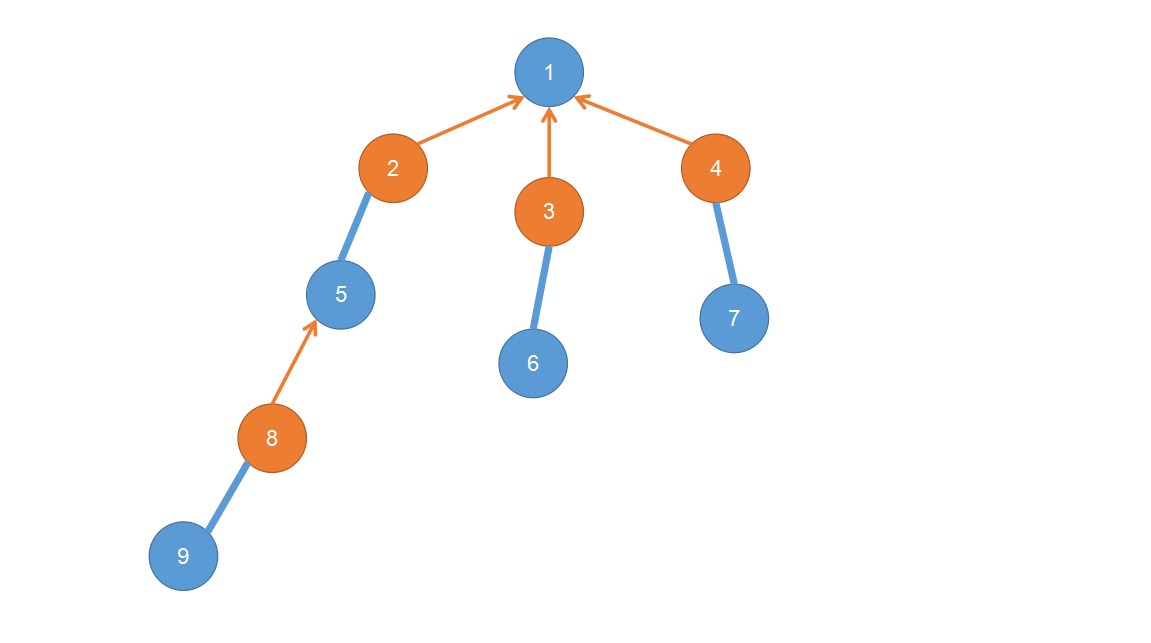
其中1号点就是我们尝试增广的节点,在这里我们给每一个节点一个(type)值,若该点不在交错树中,它的(type)值为(0),否则为(1)或(2)。上图中我们用蓝色点代表(type=1)的点,橙色点代表(type=2)的点,不难看出(type)值的不同其实代表了一种类似于二分图的关系,每个点在交错树中只和(type)值不同的点相连。当我们没有找到奇环的时候,(type)值和二分图是等价的。
那么仿照匈牙利的过程,我们将尝试增广的点(v)的(type)值设为(1)并开始增广,假设当前处理的点为(u):
1、如果(type_u=0),就代表它不在交错树中:
当(u)已经有匹配时,我们就扩展这棵交错树,将(type_u)的值设为(2)(因为其和(type)值为(1)的(v)相邻),并将(type_{match_u})的值设为(1)(同理)。这时我们就可以把(match_u)塞进队列里了,如果能够沿着(match_u)找到增广路的话我们就可以让(match_u)匹配那个增广的点并将(u)与(v)匹配,这样就使匹配数增加了(1)。同时我们将(u)的前驱(用(pre_u)表示)设置为(v),这是为了方便在找到增广路以后一路返回修改匹配。
当(u)并没有匹配时,我们就成功找到了一条增广路,此时沿着由(pre)和(match)连成的边一路修改就增广完成了,返回。
2、如果(type_u=2),代表你找到了一个偶环,并没有什么用,就跳过这个点。
3、这里是最重点的,如果(type_u=1),代表你找到了一个奇环,这就代表你的(type)值不再等价于二分图了,我们这个时候就可以开始“缩花”操作,将我们找到的奇环缩成一个点。让我们具体的考虑一下:
首先,快速找到哪些点在这个奇环中,显然(u)和(v)一定都出现在交错树上((type)不为(0)),结合上面的那张图考虑,奇环的范围就是两个点在交错树上的链中包含的所有点,因此我们需要找到这两个点的(lca),这里直接采用暴力向上跳的做法即可。
找到以后怎么连接(pre)边呢?我们参考一下文章开头的结构,可以发现此时的(lca)一定就是那个花中唯一的没有匹配或者匹配到外面节点的(1)号点。因此感性思考一下,我们应该“诱导”其他所有的点通过(pre)和(match)边一路走走到(lca)上,因此将除了与(lca)相连的(pre)边外其他的(pre)边都改为双向边,并将(u)和(v)也改成双向边即可达到这个目的。
最后做一点扫尾工作,我们可以通过并查集将奇环缩成一个点(因此在普通增广的时候也要考虑并查集的情况),不妨用(lca)做这朵花的代表。同时再考虑一下这个新点的(type)值应该设为什么,因为每个橙色点最多只有一个儿子(它的匹配点),因此(lca)一定是蓝色点,因此新点的(type)值为(1),所以要注意将花中所有(type)值为(2)的点修改为(1)并且加入队列。
当我们找不到新的点时,本次增广失败。
=分割分割==
以上就是一般图最大匹配的增广过程,注意在每次增广之前,(pre),(type)以及并查集都是要初始化的。将并查集的复杂度看作常数,则每次增广至多是(O(m))的,一共需要增广(O(n))次,因此带花树算法的复杂度和匈牙利一样,都是(O(nm)),当然,在实践中带花树算法跑得一般会比理论上界快很多。
相信在熟练理解带花树的过程后一定能写出代码,因此为了不对读者造成思维定式影响这里就不贴代码了。完结撒花~