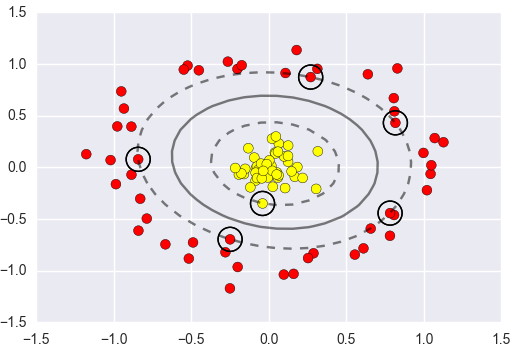
Support Vector Machine
要解决的问题:什么样的决策边界才是最好的呢?支持向量机
特征数据本身如果就很难分,怎么办呢?
计算复杂度怎么样?能实际应用吗?
目标:基于上述问题对SVM进行推导
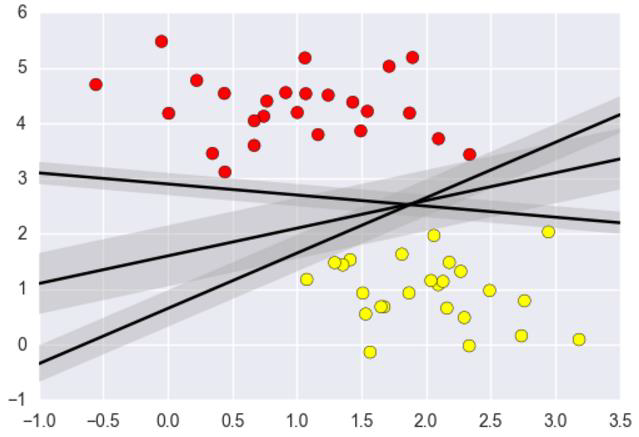
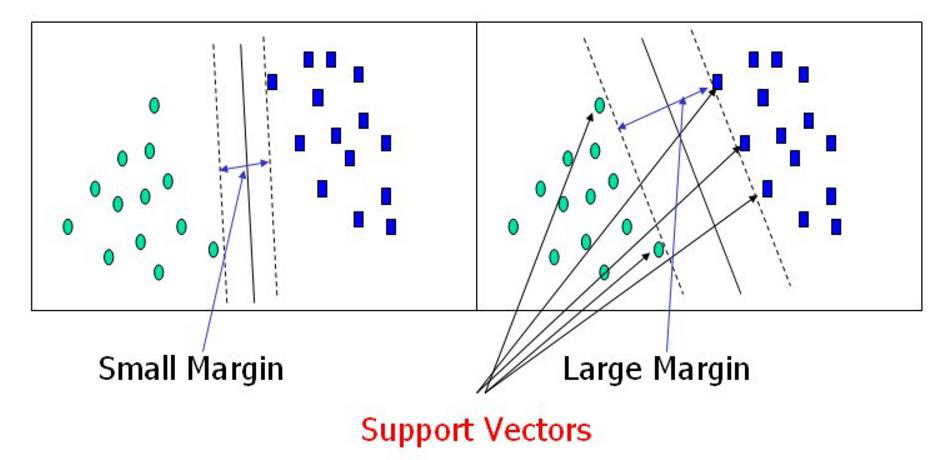
决策边界:选出来离雷区最远的(雷区就是边界上的点,要Large Margin)
距离的计算

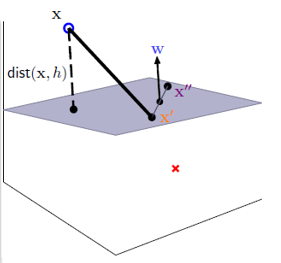
.距离 = 向量(x-x')在平面法向量(W)上的投影
![]()
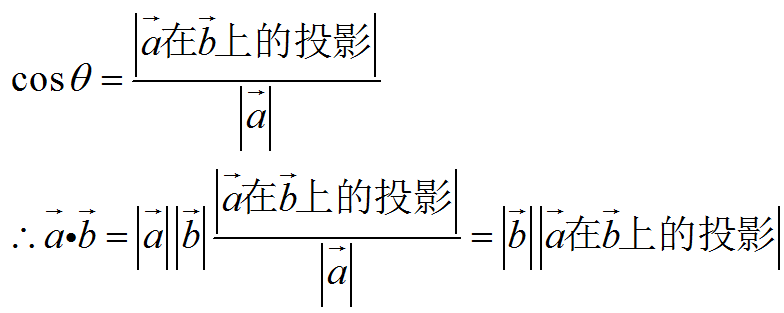
把a换成(x-x'),把b换成WT
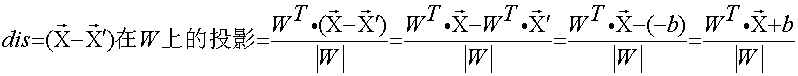
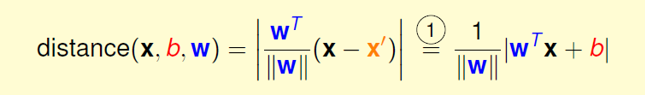
数据标签定义
数据集:(X1,Y1)(X2,Y2)…(Xn,Yn)支持向量机
Y为样本的类别:当Xi为正例时候Yi = +1 当Xi为负例时候Yi = -1
决策方程:

优化的目标
通俗解释:找到一个条线(w和b),使得离该线最近的点(雷区)能够最远
将点到直线的距离化简得:
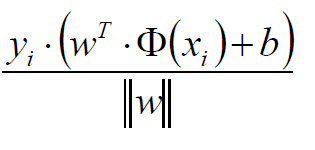
由于 所以将绝对值展开原始依旧成立
所以将绝对值展开原始依旧成立
目标函数
放缩变换:对于决策方程(w,b)可以通过放缩使得其结果值|Y|>= 1=>
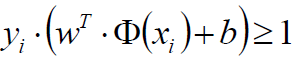 (之前我们认为恒大于0,现在严格了些)
(之前我们认为恒大于0,现在严格了些)
优化目标:
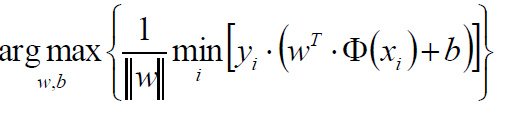
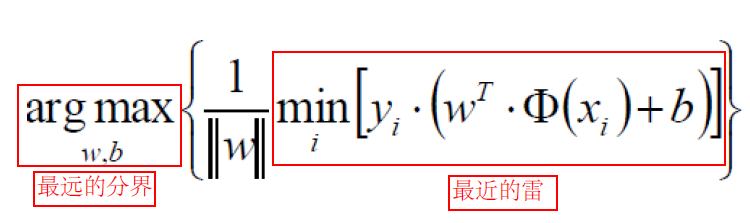
由于
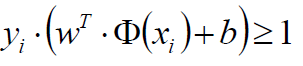
那么他的min值就是1
只需要考虑
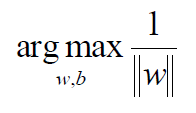
(目标函数搞定!)
自己的理解:
在决策边界的方向不变的情况下,决策边界无论离雷区(数据集)有多远,X的分布不会变,所以距离决策边界最近的X,永远是那一个
也不肯能无限远离,因为分类后,另外一类的X限制了决策边界原理的距离,
这个公式的目的在于如果分成2类A,B,那么决策边界无限远离B是不可能的,因为决策边界不可能跨越A,
目的在于将AB分开后,用来区分B的边界,无限接近于A,也就是说要一个离B最突出的点最远的分界线,
同理,用来区分A的边界,无限接近于B,也就是说要一个离A最突出的点最远的分界线。


常规套路:将求解极大值问题转换成极小值问题
1/W的最大值,也就是求W的最小值,也就是求W^2的最小值
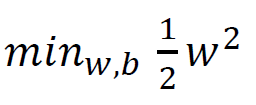
如何求解:应用拉格朗日乘子法求解
拉格朗日乘子法:
带约束的优化问题:
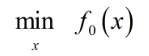
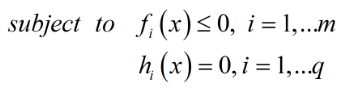
原式转换:
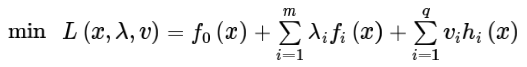
我们的式子:
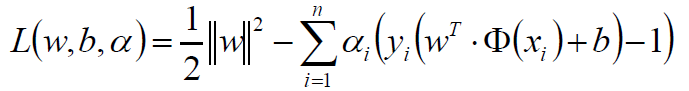
约束条件不要忘:
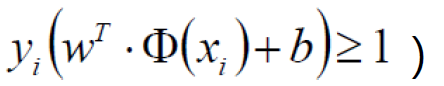
SVM求解
分别对w和b求偏导,分别得到两个条件(由于对偶性质)
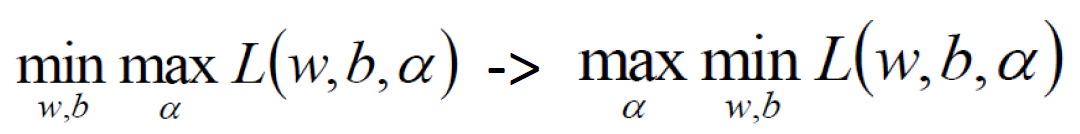
对w求偏导:
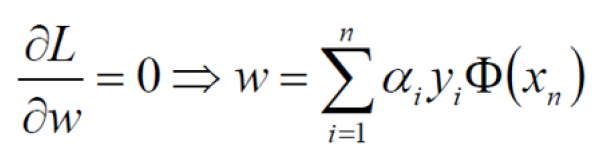
对b求偏导:
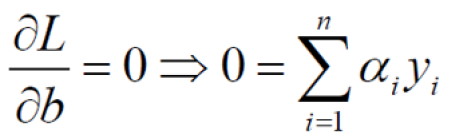
带入原始:
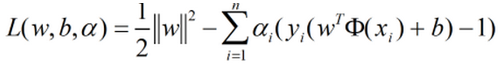
其中
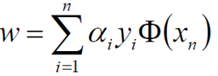

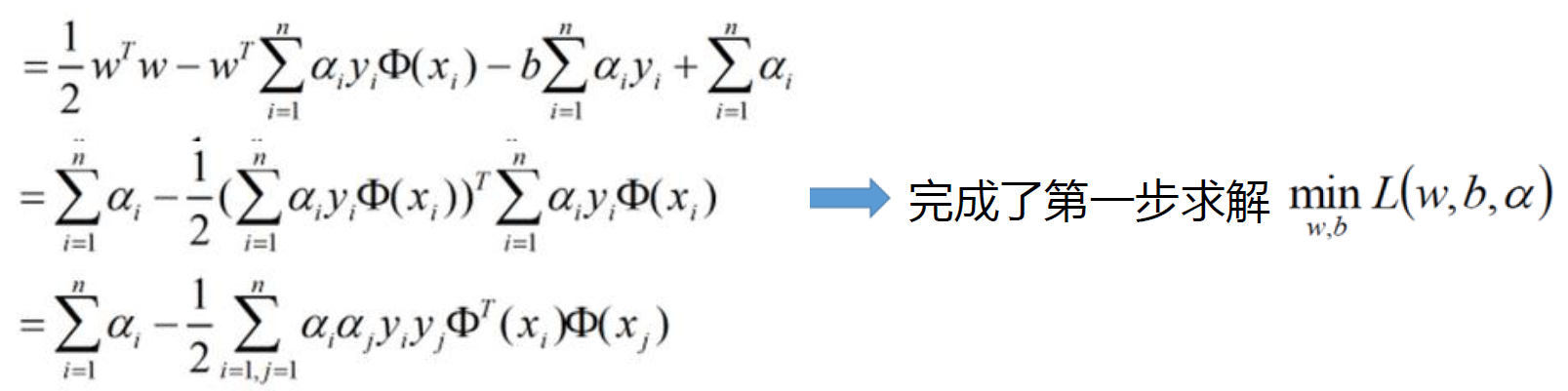
继续对ɑ求极大值:
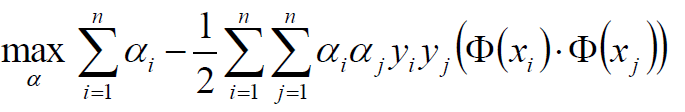
条件:
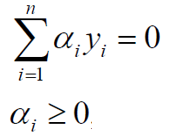
极大值转换成求极小值:

条件:
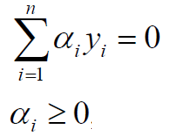
SVM求解实例
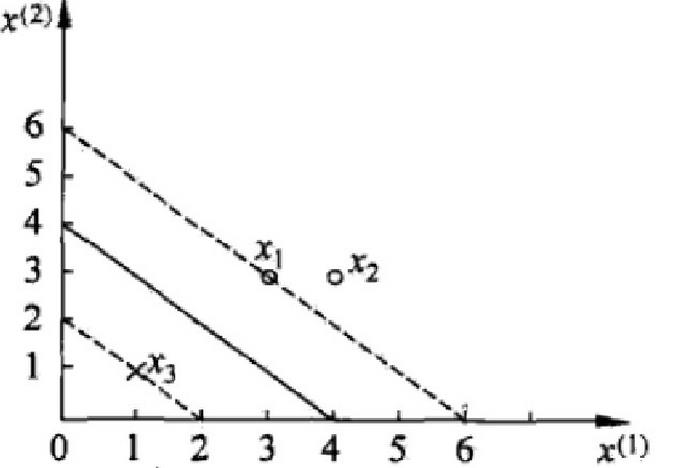
数据:3个点,其中正例X1(3,3) ,X2(4,3) ,负例X3(1,1)
求解:
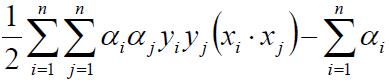
约束条件:
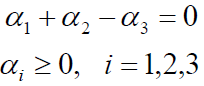
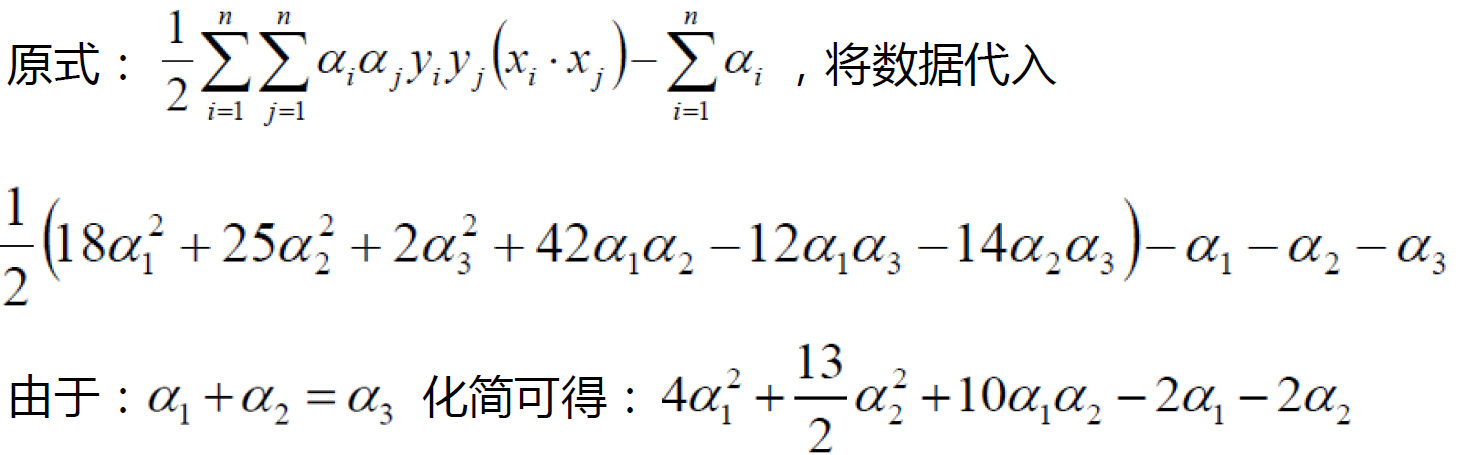
分别对ɑ1和ɑ2求偏导,偏导等于0可得:
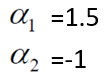
并不满足约束条件
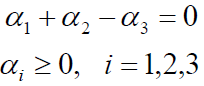
所以解应在边界上

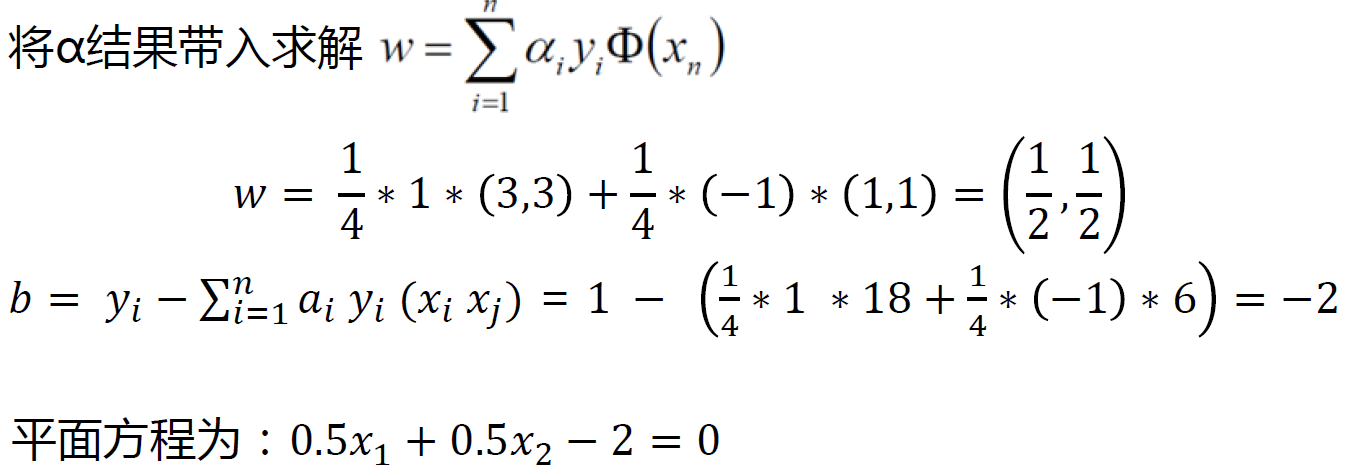
α2 = 0,叫做非支持向量,对于边界起作用的点叫做向量,也就是α不是0的点
支持向量:真正发挥作用的数据点,ɑ值不为0的点

soft-margin
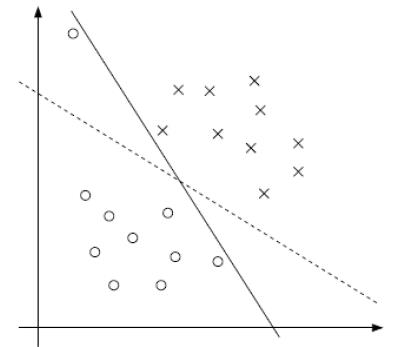
软间隔:有时候数据中有一些噪音点,如果考虑它们咱们的线就不太好了
之前的方法要求要把两类点完全分得开,这个要求有点过于严格了,我们来放松一点!
为了解决该问题,引入松弛因子
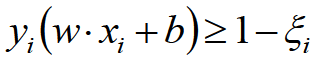
新的目标函数:
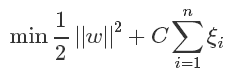
当C趋近于很大时:意味着分类严格不能有错误
当C趋近于很小时:意味着可以有更大的错误容忍
C是我们需要指定的一个参数!

低维不可分问题
核变换:既然低维的时候不可分,那我给它映射到高维呢?
目标:找到一种变换的方法,也就是![]()
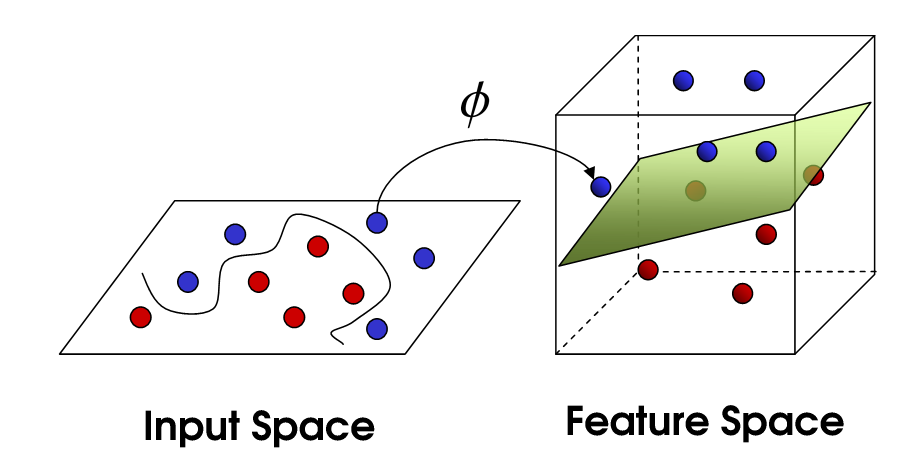
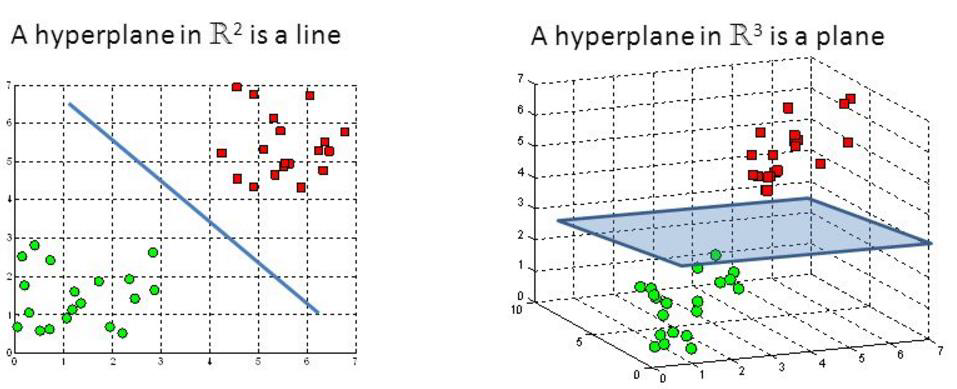

所以加上核变换的向量机就可以成为一个非线性的支持向量机了
高斯核函数:
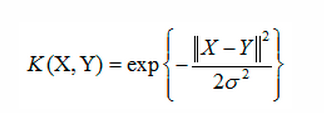
线性核函数:

高斯核函数