1.生成函数小技巧
A
不断求导可以配出$i^k$系数,每次多乘一个x,再求导,最后只会少了$a_0$
B
如果推出形如:$frac{p(x)}{q(x)}=A(x)$要求$A(x)$的递推式,其中p是n次项,q是m次项。
则$A(x)*q(x)=p(x)$利用卷积,关注$[x^n]p(x)=[x^{n-m}]A(x)*[x^m]q(x)$即可得到$a_{n-m}$,然后下顺,即可依次得到$a_{n-m-1},a_{n-m-2}...$
C
$frac{P(x)}{Pi (x-a_i)^{k_i}}$化成部分分式:$sum frac{P_i(x)}{(x-a_i)^{k_i}}$
直接通分,分子之和等于$P(x)$
即:$P(x)=sum P_i(x) imes Pi_{j!=i}(x-a_j)^{k_j}$
不妨考虑$modspace (x-a_i)^{k_i}$
可以得到:$P(x)=P_i(x) imes Pi_{j!=i}(x-a_j)^{k_j}space modspace (x-a_i)^{k_i} $
考虑进行分治处理:类似多点求值,进入左半边的时候,整体$modspace Pi_{j>mid}(x-a_j)^{k_j} $
至于还需要:$Pi_{j!=i}(x-a_j)^{k_j}$还是类似分治
再来一个多项式求逆即可得到:$Pi(x)$
用处:可以继续化简$ frac{P_i(x)}{(x-a_i)^{k_i}}=sum_{j=1}^{k_i} frac{b_j}{(x-a_i)^{j}}$
分子是一个常数,分母可以直接展开,获得这一项的O(1)公式。求通项的时候,分别对这$sum k_i$个的第$[x^n]$进行求和。O(k)求一项。胜过无脑快速递推的O(klogk)
D
$w^{i imes (n-i)}=w^{(C(n,2)-C(i,2)-C(n-i,2))}$然后除过去和n有关的。
2.
n*m的矩阵
填数
每行每列最大值必须恰好是Ci,Rj
求方案数
不妨对R,C排序,
考虑如果是<=限制,(1,1)开始,当前在$(x,y)$.设R更小,可以直接走到(R+1,C),$ans imes=R_x^{m-y+1}$也就是后面的C的个数,C更小同理。
可能无法保证最大值一定出现过。
恰好出现最大值,考虑容斥。
整体容斥很难办。按照==关系分段:$RRC<RCC<RC<RRCC$中间都是等于
每一段的填法对应往下往右这个区域的方案数。
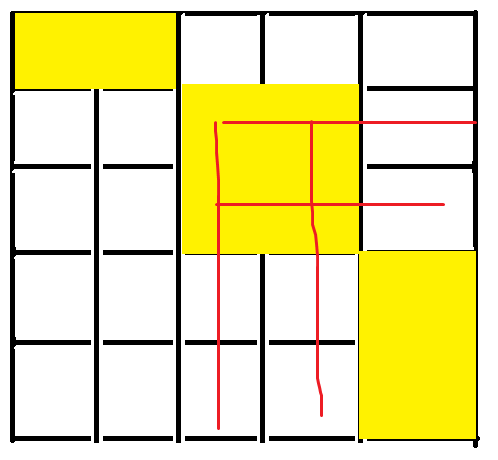
黄色部分R=C,中间的黄色区域负责处理红色的填法
显然每段独立。考虑对每段进行容斥。枚举哪些R哪些C不满足出现最大值,然后
本段有nr个R,nc个C,之后有sr个R,sc个C,限制都是v
$contribution=sum_{i=0}^{nr}sum_{j=0}^{nc} (-1)^{i+j}C(nr,i)(v-1)^{i(sc+nc)}C(nc,j)(v-1)^{j(sr+nr-i)}v^{(nr-i)(sc+nc-j)+(nc-j)(sr+nr-i)}$
NTT优化:直接放到(i+j)的位置上,形如:$v^{ij}$要用上面的技巧优化
最后每个位置加起来。
3.
构造题:
N*M棋盘,1~N*M编号各出现一次
曼哈顿距离不超过2的点对
N<=1000
度数确定4个角的点
哈希函数:一个点到4个角的最短路以及最短路方案数
然后唯一确定。。。直接还原
4.
四元环计数:[学习笔记]三元环
还是暴力,O(msqrt(m))
5.
N个点,编号0~N-1
如果popcount(i xor j) =K
连边:
i->j : weight:(ai+bj)
j->i : weight(aj+bi)
求root到各个点的最短路
考虑建立虚点优化建图
i到j xor为k,意味着把i的k位翻转
f[i][j][k]当前为i,已经确定前j位,已经翻转了k位的点
x->f[x][-1][0]->....->f[y][16][k]->y
第一条和最后一条边权为ai和bj
O(nlog^3)
优化:
1.中间的权值为0,dij取出第一个点,直接全部更新最短路
2.当k>=17/2时候,连边:x->f[(1<<17)-x][-1][0]->....->f[y][16][17-k]->y
即等价于翻回17-k次。
这样k<=17/2,状态/=2
6.
走:
(0,0,0)->(n,m,k)
到(i,j,p)有代价:Ai+Bj+Cp
求最小代价
变成差分数组{ai,bi,ci},每一步都有一个代价。
n+m+k步
考虑放abcbcbabcbabcbacb
每一步有一个带权的代价:val*后面的总步数
翻转一下,1~n往上升。每个位置i的代价:val*i
如果权值递减直接贪心
有增加的一段,一定连续放在一起(交换法证明)
并且是极长的连续一段。
权值变成平均数,接着合并(还是交换法证明)
然后变成递减的了,直接贪心
7.
程序自动分析·改:
和NOI2015相同,但是没有数据组数,只有条件,有若干组数据,恰好每组数据最后一个会不合法,把它们分开。
不能单点增量。
倍增。
每组长度为T,花费O(tlogt)的时间即可找到。
技巧:check(l,r)不支持单点加入,只能离线后处理,划分序列
倍增+二分
每次失败,但是一定可以减少2^(k-1)的规模
O(nlogn)
扩展:
给出一个有根二叉树
m个限制,n个点,2-SAT限制的关系
求每个点子树限制能否合法
树剖,从每个叶子往上按照size倍增
一个点成功了,整个子树都成功了,一个点失败了,整个到根的链都失败了
这样倍增,还是花费O(szlogsz)的时间可以解决sz大小的点。
必须按照sz倍增!否则按照深度倍增,可能突然出现很大的子树,导致进行常数极大的操作。
8.
N个点每个点度数2K(都是偶数且一样)的图,求一条哈密顿回路
Hall定理推论:一个K正则二分图一定完美匹配
跑欧拉回路定向,K入,K出
然后拆入点出点2个
找到完美匹配,直接模拟
看到度数是偶数找路径或者给边定向什么的,都可以考虑找欧拉回路
对于是入点出点的完美匹配,就是一条回路了!
9.
n个元素序列,每次删掉一个元素,左右放在一起,删完
不能中途两个相邻的数相同
求方案数
n<=500
删除问题,n<=500 考虑区间DP了
定义f[l][r][vl][vr]l-1是vl,r+1是vr,删完l,r,的方案数
其实没必要记录vl,vr,在考虑一个区间的时候,显然l-1,r+1都是不删除的。
f[l][r]l-1,r+1都没有删,先删完l,r的方案数,
枚举最后删除的转移,左右再乘上组合数分配先后顺序
发现这样设计状态也确实符合转移
扩展:
随机删除,相邻相同停下来,求步数期望
设gi为删了i个元素还没有停止的方案数
ans=∑gi/(n的i次下降幂)
求g,先做出刚才的区间DP O(n^3)
直接在序列上分段,g[i][j]表示,前i个位置,i位置不删除,删除了j个元素的方案数。枚举最后删除的一段。乘上组合数分配先后。
O(n^3)
10.
一张无向图,对于i<j<k,若i,j有边,i,k有边,那么j-k有边。
反复进行这个过程。直到停止。
有边的点对不能染相同颜色,共m种颜色,求方案数。
如果图建好之后,不妨按照编号排序,每个点的染色方案就是:m-出边个数
用并查集+set启发式合并合并边表
一个点连出去的边:1.原来就往大连的,2.连到x的更小的y,y连到比x大的那些点。
从小到大考虑,每个点x把所有连过来的点的边表合并在x上,并且用并查集表示这些边表在x这里。
然后把x-x的边删除。之后直接从连过来的点的并查集处把这些边连过来。
这样,2符合,并且不会边表里不会存在比x小的点(因为每次会删除x-x)
边表合并,set启发式合并
11.
给定l,r,M,D,求最小自然数x,使得存在y使得,l<=Dx-My<=r
y是整数,l,r,M,D是正整数,绝对值均<=1e18
对于数据都<=1e9 BSGS分块
对于数据<=1e18
等价于找到最小的y,使得存在自然数x,使得,
l<=Dx-My<=r
-r<=My-Dx<=-l
M=Dt+R
-r<=(Dt+R)y-Dx<=-l
-r<=Ry-D(-ty+x)<=-l
找到k使得y+k>0
即:Rk-r<=R(y+k)-D(-ty+x)<=Rk-l
变成找到最小的y+k,使得存在(-ty+x)
令y=y+k,-ty+x=y
可以变成子问题递归。
(类似gcd辗转相除)
O(logn)
法二
二分+类欧几里得算法:
看似是一个线性规划的感觉。
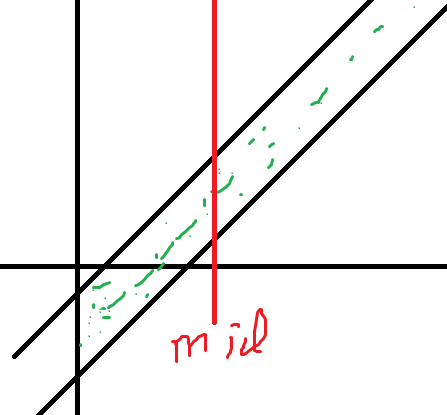
二分x,看从x=0过来的区域内有无整点。
O(log^2n)
12.
给定排列bi,维护数组ai,
支持:ai整体+1,询问$sum [frac{ai}{bi}]$中括号表下取整
总变化小于nlogn(调和级数
线段树维护每个区间下一个存在一个点+1的距离。暴力
每一次修改会到叶子,O(nlog^2)
13.
最小方差生成树
求生成树:$sum(We-A)^2$最小值,A是平均数
考虑枚举A的范围,交换排名,kruskal。过于暴力
LCT处理每个边一定能加入的区间(保留最大时间生成树,端点是(val+mi)/2),正反处理两次
然后模拟。
存疑
14.
HDU6445
给定竞赛图n<=300给没有定向的边定向,
代价计算:for(a,b,c,d互不相等)
if s(a,b)=s(b,c)=s(c,d)=s(d,a)++ans
if s(a,b)!=s(b,c);s(b,c)!=s(c,d);s(c,d)!=s(d,a)--ans
答案公式:

所有有序4元组贡献上,
无序4元组,存在一个出度为2的,不贡献,存在两个的,ans--
枚举一个点,枚举其两个出点,再枚举另一个点,这个环至少是不贡献的,会被正反枚举共8次。
发现对于两个度数为2的,恰好被扣除2次,符合倒扣ans
然后就是“石头剪刀布”那个题了。
竞赛图,考虑问题转化,变为度数的关系
15.
定义$gn(x)=Pi_{i<=n(i,n)==1}(x-w_n^i)$
$w_n$是n次单位根。求$g1(x)……g2000(x)$
反演
$fn=Pi (x-w_n^i)=x^n-1$
$fn=Pi_{d|n}g_d$
$g_d=Pi_{d|n}f_d^{mu {frac{n}{d}}}$
O(n^2logn)每次除法可以暴力O(n)进行
16.
求所有n<=300的无向连通图的1到2号点的最短路之和
到所有点在所有连通图距离和,再除以(n-1)(显然对于1到2、1到3是等价的,可以直接除以n-1)
边权为1,BFS分层图!
考虑BFS树,f(i,j,k)前i层,最后一层j,深度k,方案数。枚举下一层点数,处理这层点自己内部连边和之前最后一层连边方案。
k不必要,可以直接记到数值上。
没有在这一层的,直接整体加上n-i
f(i,j)i个点的分层图,最后一层j个点的贡献和。
g(i,j)………………………………………………的方案数
枚举下一层点数s,则连边方案乘上编号分配是:
$c=C(i+s,s) imes (2^j-1)^s imes 2^{frac{s imes(s-1)}{2}}$
转移方程:
$g[i+s][j]+=g[i][j] imes c$
$f[i+s][j]+=f[i][j] imes c+g[i][j] imes c imes (n-i-s)$最后剩下的统一加上(n-i-s)的路径。因为一定会有的。
相当于假设所有没在这i个点之中的,都一定在下一层
扩展1
贡献变成最短路平方?
$(s+1)^2=s^2+2*s+1$
考虑维护没有在这i的点中的点所有方案里面的最短路距离和t[i][j]。
发现对于每个点都是一样的,所以单独一个点其实所有方案中的最短路是:$frac{t[i][j]}{n-i}$
$g[i+s][j]+=g[i][j] imes c$
$t[i+s][j]+=frac{t[i][j]}{n-i} imes (n-s-i) imes c+g[i][j] imes c imes(n-i-s)$
$h[i+s][j]+=h[i][j] imes c+2 imes frac{t[i][j]}{n-i} imes (n-s-i) imes c +g[i][j] imes c imes(n-i-s)$
扩展2
结论:定义图的直径为两两点对最短路的最大值,则补图和原图的直径的较小值<=3,(边权为1)
考虑BFS树,两个最远点之间分层>=3时候,补图最大是3
就是相邻分层图如果是有边,那么补图就是3
17.
(了解即可)
二人博弈
n个0/1串,0号可以删除一个串的0开始的后缀,1类似。
n,m<=100
最后不能删者输
不公平博弈但是面对局面越来越差:超现实博弈?
神仙结论?
每个串权值:AAAABABB=3+0.100 1
看做二进制小数,看总和谁的更大
总和一定,后手赢
证明:每一步权值都会下降
每一次操作要么减少自己的权值,要么增大对方的权值
所以权值多的一方总能赢。
扩展?
AAB(BABAABAB)BBAB括号内重复无穷次,求解。每个串至多一个括号
小数点前无穷是inf级别,还有常数
小数点之后无穷等比数列变成常数,最后是1/inf
18.
定义$gn(x)=Pi_{i<=n(i,n)==1}(x-w_n^i)$
$w_n$是n次单位根。求$g1(x)……g2000(x)$
反演
$fn=Pi (x-w_n^i)=x^n-1$
$fn=Pi_{d|n}g_d$
$g_d=Pi_{d|n}f_d^{mu {frac{n}{d}}}$
O(n^2logn)每次除法可以暴力O(n)进行
19.
支持:
后面插入一个数,区间求xor和,整体xor,整体排序
一个前缀是排好序的,后面插入的单独记录
前缀用trie维护,后面插入还未排序的用数组记录。
区间xor和,就是找两个第k大进行前缀差分。前缀在trie树上二分即可,后面的用数组直接搞。
整体xor就是整体mark。再求区间xor时候,如果元素个数是奇数,xor上mark
插入一个数,xor上mark再插入进去。
sort?
后面合并到trie树上,但是有mark标记,使得可能顺序还有变化,
trie树整体标记mark,pushdown时左右儿子交换即可。
然后mark置零
0/1trie上可以很方便对二进制数排序,并且整体xor上,就是交换儿子。
20.
n(n<=5)个元素的序列{xn},ai<=xi<=bi,且LIS=k的方案数
bi-ai<=100
法一:爆搜+Dp?
法二:
k=1,k=5好算,APIO划艇
k=2或者k=4 DP套DP f[i][j][k]填了前i个,LIS栈里面第一个是j第二个是k方案数
k=3直接减掉
21.
CF809D
长度为n的序列{xi},n<=3e5,范围在(li,ri)之间,求LIS最长是多长
g(i,l)表示前i个数,LIS长度为l,最后一个数最小是多少(就是那个单调栈)
g(i,l)=min(g(i-1,l),xi (if exist j g(j,l-1)<x))
关于l是递增的。
虽然不知道xi是多少,
但是可以直接用(li,ri)进行计算!最后一定存在一种方法还原xi
刚好可以把一个g(i-1,l-1)+1->g(i,l)
整个区间往上平移再往右平移,再再最下面插入一个点。
实现时候,用平衡树,直接区间+1,某位置插入一个点
最后平衡树点数即为答案

#include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^'0') #define pb push_back #define solid const auto & #define enter cout<<endl #define pii pair<int,int> using namespace std; typedef long long ll; template<class T>il void rd(T &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');} template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar(' ');} namespace Miracle{ const int N=3e5+5; int n,l[N],r[N]; int tot; struct node{ int ls,rs; int ad; int val; int prio; }t[2*N]; int nc(int v){ ++tot;t[tot].val=v;t[tot].prio=rand(); t[tot].ad=t[tot].ls=t[tot].rs=0; // cout<<" nc "<<tot<<" : "<<v<<endl; return tot; } void pushdown(int x){ if(x&&t[x].ad){ t[t[x].ls].ad+=t[x].ad; t[t[x].rs].ad+=t[x].ad; t[t[x].ls].val+=t[x].ad; t[t[x].rs].val+=t[x].ad; t[x].ad=0; } } void split(int now,int &x,int &y,int k){//<=k if(!now){ x=0;y=0;return; } pushdown(now); if(t[now].val<=k){ x=now;split(t[now].rs,t[x].rs,y,k); }else{ y=now;split(t[now].ls,x,t[y].ls,k); } } int dele(int x){ pushdown(x); int rt=x; if(!t[x].ls) { // cout<<" delert "<<x<<" "<<t[x].val<<endl; return t[x].rs; } int y=0; while(t[x].ls){ // cout<<" ls "<<x<<" las "<<y<<endl; pushdown(x); y=x; x=t[x].ls; } // cout<<" dele "<<x<<" "<<t[x].val<<" "<<t[x].ls<<" "<<t[x].rs<<endl; t[y].ls=t[x].rs;return rt; } int merge(int x,int y){ if(!x||!y) return x+y; pushdown(x);pushdown(y); if(t[x].prio<t[y].prio){ t[x].rs=merge(t[x].rs,y); return x; }else{ t[y].ls=merge(x,t[y].ls); return y; } } int ans=0; void fin(int x){ if(!x) return ; pushdown(x); ++ans; fin(t[x].ls); // cout<<" x "<<x<<" : "<<t[x].val<<endl; fin(t[x].rs); } int main(){ srand(19260817); rd(n); for(reg i=1;i<=n;++i){ rd(l[i]);rd(r[i]); } int rt=0; for(reg i=1;i<=n;++i){ int x,y,p,q; split(rt,x,y,l[i]-1); split(y,p,q,r[i]-1); t[p].ad++; t[p].val++; // if(i==n) { // // cout<<" qqqq "<<endl; // fin(q); // } q=dele(q); // if(i==n) { // // cout<<" qqqq "<<endl; // fin(q); // } rt=merge(merge(merge(x,nc(l[i])),p),q); // cout<<"finfifn "<<i<<"------------------------"<<endl; // fin(rt); } ans=0; fin(rt); ot(ans); return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* */
22.
构造长度为2n的序列,使得所有前缀写出的二进制数mod 2n恰好是0~2n-1
2n个点的图,x->2x和2x+1连边,求哈密顿路径
分成x,x+n一个2个点团,(自环)(0,3)<-->(1,4)<-->(2,5)(自环)
求欧拉回路,相邻团的连边方案唯一。直接还原
23.
小公式:
给定n,$sum_{(i,n)==1}gcd(i-1,n)=phi(n)*sigma_0(n)$
用置换群理论可以证明。
设集合S={x|0<=x<n},置换:任意$(gamma ,n)=1$定义$g_{gamma}(x)=gamma * x$
该置换有元置换和置换传递性,可以构成置换群
考虑相同的x1,x2,即是否存在$gamma$使得$gamma*x_1=x_2 mod space n$
必然有gcd(x1,n)==gcd(x2,n),那么本质不同的元素(轨道数量)一共有$sigma_0(n)$个
再枚举每个置换下不动点的个数:$gamma imes x=xspace mod space n$的x的解的个数是:$gcd(gamma-1,n)$
也就是:$sigma_0(n)=frac{sum[gcd(i,n)==1] imes gcd(i-1,n)}{phi(n)}$
把分母乘过去就可以证明了。
24.
nm的0/1矩阵,每行删除一个,相邻两行删除横坐标距离不超过k
删完之后成为n(m-1)矩阵,求删完之后的矩阵本质不同方案数
n,m,k<=300

直接记录f(i,j)是不行的,显然会算重复
具体的,每行连续的1连续的0删除几个都是一样的。
所以不妨把连续的一起考虑化成若干段
考虑在字典序最小的位置统计!
也就是,能在左端点删就在左端点删。
但是k的限制,有的时候必须删中间一个。如图中的红色的圆形
这样,为了字典序最小,一定是连续每k个删除一次,直到删除到一个左端点。
这个时候就又变成叉号了。
所以f[i][j],g[i][j]O(n^3)DP即可
25.
EC Final 2018
长度为n和m的两个序列,每个位置3种可能,+1,-1,?
把?替换成-1或者+1
从(0,0)开始拿1元走,如果>=2随机上面或者下面走一步,如果是1,走+1的那一个序列,都是+1随机。如果钱==0结束
求多少种填法方案保证到(n,m)才结束
n,m<=5000
有点任意性的感觉,有一个结论:
如果存在n,m的两个位置x,y使得x-1的前缀和加上y-1的前缀和为0,并且x,y都是-1,那么不能保证
证明考虑任意性。
然后DP:即两个序列前缀最小值之和不能<=-2
两个序列相对独立了
f[i][j][k],前i个,当前最大值是j,历史最大值是k
貌似不能化简状态了
发现0的前缀和为0
考虑反过来Dp~!相对设法
f[i][j]从后往前到第i个,当前值距离历史最小值为j方案数
最后f[0][j]的j就是真实最小值了。