正经人谁学数论啊
持续更新。咕咕咕
右键数学公式(
ightarrow)Math Settings(
ightarrow)Math Renderer(
ightarrow)CommonHTML以获得更佳体验。
欢迎找锅
小学生数论,并不适合dalao
因为本人过于蒟蒻所以如果你想在这里学些什么的话还是算了
主题的锅导致标题分的不清楚,无语子
质数
Eratosthenes筛素数
其实就是劣质版线性筛,不过代码比较短,打个小表还是可以的。
时间效率(O(nlog log n))
int Pri[maxn];
bool NotPri[maxn];
void JudPri(int n){
NotPri[0]=1;
NotPri[1]=1;//全局变量大括号赋值可是很不好的习惯哦...
for(int i=2;i<=n;i++){
if(NotPri[i])continue;
Pri[++Pri[0]]=i;
for(int j=i;(long long)i*j<=n;j++)
NotPri[i*j]=1;
}
}
线性筛素数
普通版
int Pri[maxn];
bool NotPri[maxn];
void JudPri(int n){
NotPri[0]=1;
NotPri[1]=1;
for(int i=2;i<=n;i++){
if(!NotPri[i]){
Pri[++Pri[0]]=i;
}
for(int j=1;j<=Pri[0]&&i*Pri[j]<=n;j++){
NotPri[i*Pri[j]]=1;
if(i%Pri[j]==0)break;
}
}
}
无需取模版
int v[maxn],Pri[maxn];
void JudPri(int n){
for(int i=2;i<=n;i++){
if(v[i]==0){
v[i]=i;
Pri[++Pri[0]]=i;
}
for(int j=1;j<=Pri[0];j++){
if(i*Pri[j]>n||Pri[j]>v[i])break;
v[i*Pri[j]]=Pri[j];
}
}
}
可能玄学上更快?(大雾)不过可能普通版的bool数组更快也说不定呢(好像真的会快很多)。
Miller_Rabin大素数判定
(所以名字到底事Robbin还是Rabin还是Rabbin?)
前置芝士:费马小定理
注:本文仅介绍简易版写法,深入学习建议看Gary_818的博客。
是看脸的随机化算法,错误率基本趋近于0。
0202年了不会还有人(O(sqrt n))判断素数吧不会吧不会吧
这种判断素数的方法利用的是的逆命题,随机枚举一个(a),满足这个同余式,那么(p)就是素数。
不过其逆命题并不是个真命题(大雾),例如在(p=341)的时候若(a=2)满足费马小定理,然而341是一个合数((341=11 imes 31))。因此仅判断一次得到的结果不一定正确,那怎么增大正确率呢?
那就是重复判断30次
时间复杂度(O(log n))(忽略常数)
#include<bits/stdc++.h>
using namespace std;
const int count=30;
int n;
inline int qpow(int a,int b,int Mod){
int ans=1,base=a;
while(b){
if(b&1)ans=ans*base%Mod;
base=base*base%Mod;
b>>=1;
}
return ans;
}
bool Miller_Rabin(int n){
if(n==2)
return true;
for(int i=1;i<=count;i++){
int a=rand()%(n-2)+2;
if(qpow(a,n,n)!=a)
return false;
}
return true;
}
int main(){
srand(time(0));
scanf("%d",&n);
if(Miller_Rabin(n))
printf("Probably a prime.");
else
printf("A composite.");
printf("
");
return 0;
}
约数
GCD
辗转相除法求GCD
各位dalao已经倒着都能写了。
辗转相除法求最大公约数。或者为了防止爆栈可以改成循环。
inline int gcd(int x,int y){
if(y==0)return x;
else return(y,x%y);
}
二进制方法求GCD
如果想优化(可能大数据可以优化几百(mathrm{ms}))
就变成魔法少女就可以用二进制优化(不过平时基本也无用)
- (a),(b)为偶数,则(gcd(a,b)=2 imes gcd(a/2,b/2))。
- (a)为奇数,(b)为偶数,则(gcd(a,b)=gcd(a,b/2))。
- (a),(b)为奇数。假设(ageq b),则(gcd(a,b)=gcd((a-b)/2,b))。
- (a)为(0),则返回(b)。
可以用手写abs和min卡常
inline ll abs(ll x){
return x<0?-x:x;
}
inline ll min(ll a,ll b){
return a<b?a:b;
}
inline ll gcd(ll a,ll b){
if(a==0)return b;
if(b==0)return a;
if(!(a&1)&&!(b&1))return 2*gcd(a>>1,b>>1);
else if(!(a&1))return gcd(a>>1,b);
else if(!(b&1))return gcd(a,b>>1);
else return gcd(abs(a-b),min(a,b));
}
没有取模操作会快很多。
更相减损术求GCD
懒得写,建议BFS。
高精度运算的时候可以用(不过既然都是要用高精度的题了为何不弃了呢)
裴蜀定理
设(a,b)是全不为零的整数,则存在整数(x,y),使得(ax+by=gcd(a,b))。
算数基本定理的推论
算数基本定理(唯一分解定理)
任意大于1的正整数(N)都可分解为有限个素数的乘积。
(N=p_1^{c_1}p_2^{c_2}p_3^{c_3}cdots p_m^{c_m})
其中(c_i)都是正整数,(p_i)都是素数且满足(p_1<p_2<p_3⋯<p_m)。
求正约数个数
(N)的正约数个数为(prodlimits^m_{i=1}(c_i+1))
线性筛求约数个数
void pre(){
d[1]=1;
for(int i=2;i<=n;i++){
if(!v[i])v[i]=1,p[++tot]=i,d[i]=2,num[i]=1;
for(int j=1;j<=tot&&i<=n/p[j];j++){
v[p[j]*i]=1;
if(i%p[j]==0){
num[i*p[j]]=num[i]+1;
d[i*p[j]]=d[i]/num[i*p[j]]*(num[i*p[j]]+1);
break;
}else{
num[i*p[j]]= 1;
d[i*p[j]]=d[i]*2;
}
}
}
}
约数和定理
(N)的所有正约数之和为(prodlimits^m_{i=1}(sumlimits^{c_i}_{j=0}(p_i)^j))
线性筛求约数和
(f_i)表示(i)的约数和,(g_i)表示(i)的最小质因子(p+p^1+p^2+dots +p^k)
void pre(){
g[1]=f[1]=1;
for(int i=2;i<=n;i++){
if(!v[i])v[i]=1,p[++tot]=i,g[i]=i+1,f[i]=i+1;
for (int j=1;j<=tot&&i*p[j]<=n;j++){
v[i*p[j]]=1;
if(i%p[j]==0){
g[i*p[j]]=g[i]*p[j]+1;
f[i*p[j]]=f[i]/g[i]*g[i*p[j]];
break;
}else{
f[i*p[j]]=f[i]*f[p[j]];
g[i*p[j]]=1+p[j];
}
}
}
for(int i=1;i<=n;i++)
f[i]=(f[i-1]+f[i])%Mod;
}
求正约数集合
一个大于1的正整数(N)的正约数集合可写作
试除法
时间效率(O(sqrt n))。不会有人不会吧不会吧不会吧。
倍数法
倍数法以(O(nlog n))的效率求出(1-n)所有数的正约数集合,比试除法的(O(nsqrt n))快很多。
vector<int> fac[maxn];
for(int i=1;i<=n;i++)
for(int j=1;i*j<=n;j++)
fac[i*j].push_back(i);
欧拉函数
(1-N)中与(N)互质的数的个数称为欧拉函数。
性质
建议去看虎哥博客(懒得粘)
分解质因数求单个欧拉函数
这不是有手就行吗
Eratosthenes筛求欧拉函数
妹想到吧又事它,时间效率(O(nlog n)),虽然效率不高但是很短(?)
int phi[maxn];
void Euler(int n){
for(int i=2;i<=n;i++)
phi[i]=i;
for(int i=2;i<=n;i++)
if(phi[i]==i)
for(int j=i;j<=n;j+=i)
phi[j]=phi[j]/i*(i-1);
}
线性筛求欧拉函数
这不是有手就行吗
扩展欧几里得
深入学习建议看YouXam的博客。
扩展欧几里德定理(Extended Euclidean algorithm, EX(恶心)GCD)。
用于求(ax+by=gcd(a,b))的一组整数解。
int exgcd(int a,int b,int &x,int &y) {
if (b==0){
x=1;
y=0;
return a;//a为最大公约数
}
int ret=exgcd(b,a%b,x,y);
int t=x;
x=y;
y=t-a/b*y;
return ret;
}
设(gcd(a,b)=d),对于更一般的方程(ax+by=c),它有解当且仅当(d|c)。可以先求出(ax+by=d)的一组特解(x_0,y_0),使其同时乘上(frac{c}{d}),就得到了(ax+by=c)的一组特解(frac{c}{d}x_0,frac{c}{d}y_0)。
即(ax+by=c)通解可以表示为:
非平凡因子
若(x)能整除(n)且(1<x<n),则(x)是(n)的非平凡因子。
即一个数除1和本身外的约数。
质数没有非平凡因子。
Pollard_Pho大数字质因数分解
请先了解Miller_Rabin大素数判定算法。
Pollard Rho是一个非常玄学的方式,用于在(O(n^{1/4}))的期望时间复杂度内计算合数n的某个非平凡因子。事实上算法导论给出的是(O(sqrt p)),(p)是(n)的某个最小因子,满足(p)与(n/p)互质。但是这些都是期望,未必符合实际。但事实上Pollard Rho算法在实际环境中运行的相当不错。
Pollard_Rho算法的大致流程是:先判断当前数是否是素数(Miller_Rabin)了,如果是则直接返回。如果不是素数的话,试图找到当前数的一个因子(可以不是质因子)。然后递归对该因子和约去这个因子的另一个因子进行分解。
即找到一个数(s)使(1<gcd(s,x)<x),此时(X)可以被分解为(gcd(s,x))和(frac{x}{gcd(s,x)})两部分递归处理。
那么怎么找到当前数(n)的一个因子呢,没错又事看脸的随机化算法(大雾),感觉有一点“试”的感觉。
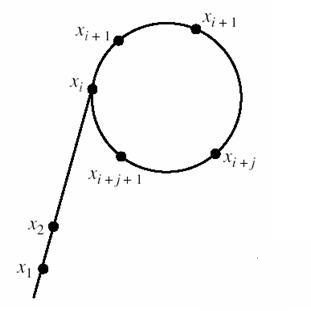
我们(rand())一个(1-x-1)内的数字设为(v_0),此时使(v_i=(v_{i-1}^2+t)\%x)直至(v_i=v_0)((t)自己设定,例如114514一般设定成1就可以,但尽量不要设置成0或2)。(这其实是一个剩余系)
由于它某项的值仅由前一项决定,且每一项可能的取值是有限的,因此该数列一定会在经历一定次数的迭代后陷入循环,形成一个类似希腊字母rho((
ho))的形状,因此得名。
生日悖论:
23 个人里有两个生日相同的人的概率有多大呢?居然有 50%。不计特殊的年月,如 2 月 29 日。于是一年中有 N = 365 天。设房间里有 n 个人,要计算所有人的生日都不相同的概率。那么第一个人的生日是 365 选 365,第二个人是 365 选 364,第三个人 365 选 363 …… 第 n 个人的生日是 365 选 365-(n-1)。所以所有人生日都不相同的概率为[frac{365!}{365^n(365-n)!} ]可以看到n=100远小于N=365 时,就已经几乎必然有一对同生缘,所有人生日两两不同的概率仅一千万分之三。
N=365天中要出现两个生日相同的人,所需人数为(n-O(sqrt N))量级。
(懒得排版了,详细可以B(aidu)FS)
因此要求出现一对相同的数,其长度就大致为(sqrt n)。
当(v_iequiv v_jpmod p,v_i
ot=v_j)时,则(p|(vert v_i-v_jvert ))。计算(gcd(vert v_i-v_jvert ,p))即可达到一个(x)的非平凡因子(p)。
简易的实现方式:
设一个在环上的定点(u)和动点(v),经过多次迭代(约为(x^{1/4}))必定能找到(uequiv vpmod p)。
为了使(u)在环上,使其标号倍增。
ll Pollard_Rho(ll x){
ll v=rand(0,x-1);
ll u=v,d=1,i=0,temp=2;
while(d==1){
v=(v*v+1)%x;
d=gcd((ll)fabs(u-v),x);
i++;
if(i==temp){
u=v;//倍增
temp<<=1;
}
}
return d;
}
模板 Pollard-Rho算法
本题时间限制很紧,需要使用Floyed判环和倍增积累(gcd)。而且数据范围很大,需要使用__int128(所以看看就好)
基于Floyed的实现:
(然而并不知道和Floyed有什么关系?求指教)
使点(u,v)在同一起点出发,使(u)一倍速度迭代,(v)二倍速度迭代,当(uequiv vpmod p)就找到了环。这种方法比倍增方法快很多。
ll Pollard_Rho(ll x){
if(x==4)return 2;
ll u=rand(0,x-1),v=u;
ll d=1;
u=(u*u+1)%x;
v=(v*v+1)%x;v=(v*v+1)%x;
while(u!=v){
u=(u*u+1)%x;
v=(v*v+1)%x;v=(v*v+1)%x;
d=gcd((ll)fabs(u-v),x);
if(d!=1)return d;
}
return x;
}
倍增积累GCD:
每次的(vert u-vvert),若存在(p|(vert u_i-v_ivert)),则对于多个(vert u-vvert)的乘积(Mul),仍满足(p|Mul)。
因此我们可以先积累一定的答案再做(gcd),毕竟(gcd)不是(O(1))的。
ll Pollard_Rho(ll x){
if(x==4)return 2;
ll u=rand(0,x-1),v=u;
ll d=1;
u=(u*u+1)%x;
v=(v*v+1)%x;v=(v*v+1)%x;
for(int i=1;u!=v;i=min(128,i<<1)){
ll Mul=1;
for(int j=0;j<i;j++){
ll temp=Mul*(ll)fabs(u-v)%x;
if(!temp)break;//abs(u-v)%x=0
Mul=temp;
u=(u*u+1)%x;
v=(v*v+1)%x;v=(v*v+1)%x;
}
d=gcd(Mul,x);
if(d!=1)return d;
}
return x;
}
本题ACGG代码:
博主已经调了一下午了还没有调出来qwq
有锅代码,求dalao帮调错。
#include<bits/stdc++.h>
#define DEBUG puts("FUCK")
#define int long long
using namespace std;
typedef long long ll;
const int cnt=30;
int n,Max;
inline int read(){
int x=0,fopt=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-')fopt=-1;
ch=getchar();
}
while(isdigit(ch)){
x=(x<<3)+(x<<1)+ch-48;
ch=getchar();
}
return x*fopt;
}
int gcd(int a,int b){
if(b==0)return a;
return gcd(b,a%b);
}
inline int qmul(int a,int b,int Mod){
int c=a*b/Mod;
int ans=a*(long double)b-c*Mod;
if(ans<0)ans+=Mod;
if(ans>=0)ans-=Mod;
return ans;
}
inline int qpow(int a,int b,int Mod){
int ans=1,base=a;
while(b){
if(b&1)ans=ans*base%Mod;
base=base*base%Mod;
b>>=1;
}
return ans;
}
bool Miller_Rabin(int x){
if(x<2)return false;
if(x==2||x==3)
return true;
for(int i=1;i<=cnt;i++){
int a=rand()%(n-2)+2;
if(qpow(a,x,x)!=a)
return false;
}
return true;
}
inline int Plus(int a,int b,int Mod){
int c=a+b;
if(c>=Mod)return c-Mod;
else return c;
}
inline int Getnext(int v,int c,int x){
return Plus(qmul(v,v,x),c,x);
}
inline int Abs(int x){
return x<0?-x:x;
}
int Pollard_Rho(int x){
if(x==4)return 2;
int u=Abs(rand()%(x-1)),v=u,d=1;
u=Getnext(u,1,x);
v=Getnext(v,1,x);v=Getnext(v,1,x);
for(int i=1;u!=v;i=min((int)128,i<<1)){
int Mul=1;
for(int j=0;j<i;j++){
int temp=qmul(Mul,Abs(Plus(u,-v,x)),x);
if(!temp)break;
Mul=temp;
u=Getnext(u,1,x);
v=Getnext(v,1,x);v=Getnext(v,1,x);
}
d=gcd(Mul,x);
if(d!=1)return d;
}
return x;
}
inline void Upd(int p){
if(p>Max)Max=p;
}
void dfs(int x){
srand(time(0));
int a=Pollard_Rho(x);
while(a!=x)a=Pollard_Rho(x);
int b=x/a;
if(Miller_Rabin(a))Upd(a);
else dfs(a);
if(Miller_Rabin(b))Upd(b);
else dfs(b);
}
int Getans(int x){
Max=0;
if(Miller_Rabin(x))
return x;
else dfs(x);
return Max;
}
signed main(){
srand(time(0));
int T=read();
while(T--){
n=read();
int Ans=Getans(n);
if(Ans==n)puts("Prime");
else printf("%lld
",Ans);
}
return 0;
}
同余
费马小定理
不是小费马定理
前置芝士
剩余类&剩余系:总之大概就是一些数(mathrm{mod})一个正整数(n)之后都能得到什么结果(敷衍),最常用的完全剩余系({0,1,…,n-1})。
正文
若(p)为素数,且(a)不是(p)的倍数则:
另一个形式:若(p)为素数,对于任意整数(a):
证明:不会。建议记住(雾)。补上了
注:以下费马小定理、二次探测定理、威尔逊定理证明摘自博客。
考虑(1,2,3...(p - 1))共(p-1)个数字,给所有数字同时乘(a),得到(a,2a,3a,...(p - 1)a)
欧拉定理
当模数为合数的时候需要用范围更广泛的欧拉定理。
若(gcd(a,m)=1),则:
扩展欧拉定理
证明
(好像没用过)
二次探测定理
若(p)为质数且(xin(0,p)),则方程(x^2 equiv 1pmod p)的解为(x = 1, x = p - 1)。
证明:
Wilson定理
当且仅当(p)为素数时:(( p -1 )! ≡ -1 pmod p)
乘法逆元
众所周知同余不满足同除性,所以数学家们弄出了逆元这个东西。
若整数(b,m)互质,且(b|a),则存在一个整数(x),使得(a/bequiv a imes xpmod m),则称(x)是(b)的模(m)的乘法逆元,记为(b^{-1}pmod m)。
可见并不是所有数都存在逆元。
费马小定理求逆元
即(a^{p-2}pmod p)。快速幂求解,很方便。
前提条件:模数为素数,且(a)不是(p)的倍数。有的题特意卡这个,例如沙拉公主的困惑。
欧拉定理求逆元
即(a^{varphi(p)-1}pmod p)
扩展欧几里得求逆元
求Exgcd(a, p)(
ightarrow)利用扩展欧几里得算法不断递归直到x=1,y=0(
ightarrow)反向递归求出第一层的x和y,x即为a模p的逆元。
前提条件:(a)和(p)互质。
#include<bits/stdc++.h>
using namespace std;
int b,x,y,mod;
inline int exgcd(int a,int b,int &x,int &y){
if(b==0){
x=1;
y=0;
return a;
}
int ret=exgcd(b,a%b,x,y);
int t=x;
x=y;
y=t-(a/b)*y;
return ret;
}
int main(){
scanf("%d%d",&b,&mod);
int gcd=exgcd(b,mod,x,y);
if(gcd!=1)
printf("None
");
else
printf("%d
",(x%mod+mod)%mod);
return 0;
}
线性求逆元
建议背式子
inv[1]=1;
for(int i=2;i<=n;i++)
inv[i]=(p-p/i)*inv[p%i]%p;
线性同余方程
(蒟蒻表示并不会高次的)
形如(axequiv ypmod b)的方程被称为线性同余方程。
模板
定理1:(ax+by=ciff axequiv cpmod b),有整数解的充要条件是(gcd(a,b)|c)。
因此我们可以先用扩展欧几里得算法求出一组特解(x_0,y_0),则(ax_0+by_0=
gcd(a,b))。此时两边同除(gcd(a,b)),再同乘(c)。得到(acfrac{x_0}{gcd(a,b)}+bcfrac{y_0}{gcd(a,b)}=c)。我们就得到了一个解(frac{x_0c}{gcd(a,b)})。
定理2:若(gcd(a,b)=1),且(x_0,y_0)为(ax+by=c)的一组解,则该方程的任意解可表示为(x=x_0+bt,y=y_0-at (tin mathbb{Z}))。
根据定理2求出的最小整数特解为:
方程的通解则是所有模(frac{b}{gcd(a,b)})与(x)同余的整数。
int exgcd(int a,int b,int &x,int &y){
if(b==0){
x=1;
y=0;
return a;
}
int d=exgcd(b,a%b,x,y);
int t=x;
x=y;
y=t-a/b*y;
return d;
}
bool Cal(int a,int b,int c,int &x,int &y){
int d=exgcd(a,b,x,y);
if(c%d!=0)return 0;
int k=c/d;
x*=k;
y*=k;
return 1;
}
中国剩余定理
有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?
即求满足以下条件的整数:除以(3)余(2),除以(5)余 (3),除以(7)余(2)。
中国剩余定理(CRT)可求解如下形式的一元线性同余方程组(其中(n_1,n_2,dots,n_k)两两互质)。
- 计算所有的模数的积(n);
- 对于第(i)个方程:
- 计算(m_i=frac{n}{n_i});
- 计算(m_i)在模(n_i)意义下的逆元(m_i^{-1});
- 计算(c_i=m_im_i^{-1})(不要对(n_i)取模)
- 方程的唯一解为:(a=sumlimits^k_{i=1}a_ic_ipmod n)
扩展中国剩余定理
只考虑两个方程,多个方程可以两两合并。
设两个方程分别为(xequiv a_1pmod {m_1})、(xequiv a_2pmod {m_2})
将其转为不定方程:(x=m_1p+a_1=m_2q+a_2 (p,qinmathrm{Z}))
则有(m_1p-m_2q=a_2-a_1)。
由裴蜀定理,(gcd(m_1,m_2)
ot|(a_2-a_1))时无解。
其他情况可通过扩展欧几里得算法求出一组可行解((p,q))。
则原两方程组成的模方程组的解为(xequiv m_1p+a_1pmod {mathrm{lcm}(m_1,m_2)})
组合数学相关
仅挖坑
Catalan数
Lucas定理
莫比乌斯反演&&拉格朗日插值
建议问(liuchanglc)(滑稽)