已知(O)为坐标原点,圆(M:(x+1)^2+y^2=1),圆(N:(x-2)^2+y^2=4).(A,B)分别为圆(M)和圆(N)上的动点,则(S_{ riangle OAB})的最大值为(underline{qquadqquad}).
解析:
法一 如图,若固定(A)的位置,则当(B)位于如图所示位置时,(S_{ riangle OAB})的面积最大,
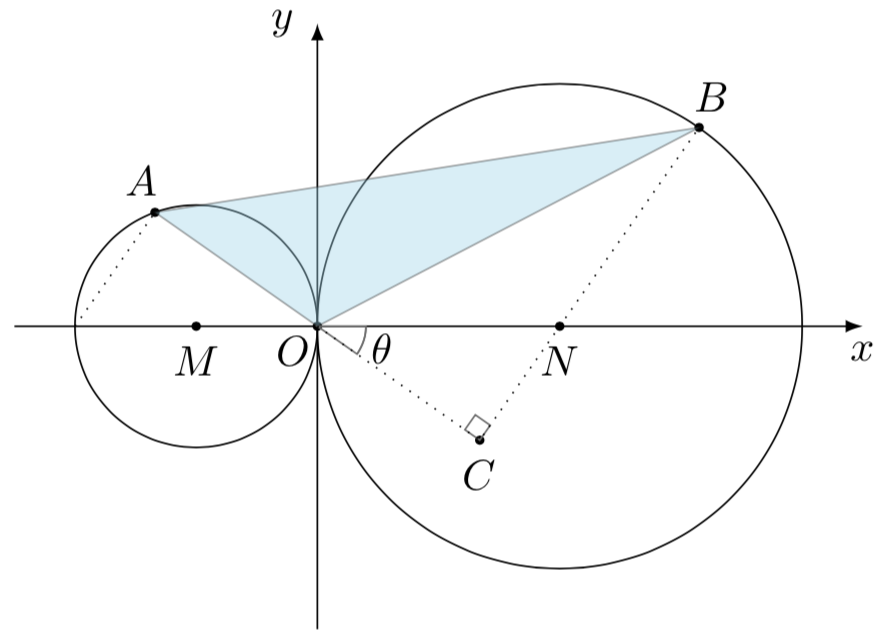
&S_{ riangle OAB}
=&dfrac{1}{2}cdot |OA|cdot |BC|
=&dfrac{1}{2}cdot |OC|cdot left(|NC|+|NB| ight)
=&dfrac{1}{2}cdot |ON|cos hetacdotleft( |ON|sin heta+|NB| ight)
=&2cos hetaleft(1+sin heta ight)
=&2sqrt{cos^2 hetacdotleft(1+sin heta ight)^2}
=&2sqrt{left(1-sin heta ight)left(1+sin heta ight)^3}
=&2sqrt{dfrac{1}{3}cdot left(3-3sin heta ight)left(1+sin heta ight)^3}
leqslant& 2sqrt{dfrac{1}{3}cdot left[dfrac{left(3-3sin heta ight)+left(1+sin heta ight)+left(1+sin heta ight)+left(1+sin heta ight)}{4} ight]^2 }
=&dfrac{3sqrt{3}}{2}.
end{split}$$
因此当(sin heta=dfrac{1}{2})时,所求面积取得最大值(dfrac{3sqrt3}{2}).
法二 同法一,可得$$
S_{ riangle OAB}=2cos hetaleft(1+sin heta ight).$$设上述表达式为(y=f( heta), hetainleft[0,dfrac{pi}{2} ight)),求导可得$$
f'( heta)=2left(1-2sin heta ight)left(1+sin heta ight), hetainleft[0,dfrac{pi}{2} ight).$$因此当( heta=dfrac{pi}{6})时,(f( heta))也即(S_{ riangle OAB})取得最大值(dfrac{3sqrt{3}}{2}).